Відмінності між версіями «Діжка Паскаля»
| Рядок 22: | Рядок 22: | ||
Якщо прийняти висоту води в трубці 4 метра (балкон другого поверху), діаметр бочки 0,8 м, і висоту бочки 0,8 м. Яка сила розриває бочку? | Якщо прийняти висоту води в трубці 4 метра (балкон другого поверху), діаметр бочки 0,8 м, і висоту бочки 0,8 м. Яка сила розриває бочку? | ||
| − | == | + | == Розв'язання == |
[[Зображення:000002.jpg |150px|right|thumb|]] | [[Зображення:000002.jpg |150px|right|thumb|]] | ||
Версія за 20:35, 12 листопада 2015
Діжка Паскаля
Блез Паскаль- французький філософ, письменник, фізик, математик. Паскаль народився 19 червня 1623 року в місті Клермон-Ферра
- З дитинства проявляв неймовірні знання з математики, в 16 років сформулював одну з основних теорем проективної геометрії (теорема Паскаля)
Дослід з діжкою
За вказівкою Паскаля, міцну дубову діжку до країв наповнили водою і наглухо закрили кришкою.
- У невеликий отвір в кришці заклали кінець вертикальної скляної трубки такої довжини, що кінець її виявився на рівні другого поверху.
Вийшовши на балкон, Паскаль взявся наповнювати трубку водою. Не встиг він вилити і десятка склянок, як раптом, на подив обступивших бочку роззяв, бочка з тріском лопнула. Її розірвала незрозуміла сила
Задача
- Бочка Паскаля
Якщо прийняти висоту води в трубці 4 метра (балкон другого поверху), діаметр бочки 0,8 м, і висоту бочки 0,8 м. Яка сила розриває бочку?
Розв'язання
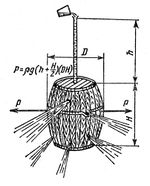
На поверхні води в бочці під кришкою це тиск P = pgh,
де p - щільність води
- g - прискорення вільного падіння,
- h - висота стовпа води в трубці.
Помноживши тиск на площу діаметрального перетину бочки (S = D * H, Н - висота бочки), одержимо силу, яка розтрощила її міцні дубові стінки: P = pg (h + H / 2) DH = 27,6 кН. Паскаль переконується: так, сила, розірвала бочку, зовсім не залежить від кількості води в трубці. Вся справа в висоті, до якої трубка була заповнена Далі проявляється дивна властивість води - передавати тиск, створюваний на її поверхні (в бочці) по всьому об'єму, кожній точці стінки або дна бочки.
- Так він приходить до відкриття закону, що отримав його ім'я.