Відмінності між версіями «Рівняння Бернуллі для елементарної струминки реальної рідини»
Tamilka (обговорення • внесок) (→Виведення рівняння Бернуллі для елементарної струминки в'язкої рідини) |
Tamilka (обговорення • внесок) (→Виведення рівняння Бернуллі для елементарної струминки в'язкої рідини) |
||
| Рядок 51: | Рядок 51: | ||
<math>z_{1}+\frac{p_{1}}{\rho g}+\frac{U_{1}^{2}}{2g}=z_{2}+\frac{p_{2}}{\rho g}+\frac{U_{2}^{2}}{2g}</math> | <math>z_{1}+\frac{p_{1}}{\rho g}+\frac{U_{1}^{2}}{2g}=z_{2}+\frac{p_{2}}{\rho g}+\frac{U_{2}^{2}}{2g}</math> | ||
| − | Сума <math>z+\frac{p}{\rho g}</math> являє собою потенційну енергію, що складається з питомої енергії положення z і питомої енергії тиску <math>\frac{p}{\rho g}</math>. Вираз <math>\frac{U^{2}}{2g}</math> називається питомою кінетичної енергією. | + | Сума <math>z+\frac{p}{\rho g}</math> являє собою потенційну енергію, що складається з питомої енергії положення <math>z</math> і питомої енергії тиску <math>\frac{p}{\rho g}</math>. Вираз <math>\frac{U^{2}}{2g}</math> називається питомою кінетичної енергією. |
| + | |||
| + | Вздовж елементарної струминки питомі кінетична і потенційна енергії можуть змінюватися, але їхня сума залишається постійною. | ||
| + | |||
| + | При русі в'язкої рідини сумарна питома енергія рідини, яка рухається вздовж струминки, зменшується в силу різних гідравлічних опорів. Отже, для елементарної цівки в'язкої рідини, що знаходиться в сталому русі: | ||
| + | |||
| + | <math>z_{1}+\frac{p_{1}}{\rho g}+\frac{U_{1}^{2}}{2g}> z_{2}+\frac{p_{2}}{\rho g}+\frac{U_{2}^{2}}{2g}</math> | ||
| + | |||
| + | Щоб отримати рівність лівої і правої частини, необхідно в правій частині додати додатковий член <math>hz</math>, що позначає витрату питомої енергії на подолання опорів при русі реальної в'язкої рідини в межах між першим і другим перерізами. У цьому випадку рівняння Бернуллі приймає вигляд: | ||
| + | |||
| + | <math>z_{1}+\frac{p_{1}}{\rho g}+\frac{U_{1}^{2}}{2g}=z_{2}+\frac{p_{2}}{\rho g}+\frac{U_{2}^{2}}{2g}+h_{\sum _{1\rightarrow 2}} | ||
| + | </math> | ||
Версія за 15:56, 31 травня 2011
Рівня́ння Берну́ллі (рос. уравнение Бернулли; англ. Bernoulli's theorem; нім. Bernulligleichung) — рівняння гідроаеромеханіки, яке визначає зв'язок між швидкістю v рідини, тиском p в ній та висотою h частинок над площиною відліку. Рівняння Бернуллі виражає закон збереження енергії рухомої рідини. Застосовується в гідравліці і гідродинаміці. Виведене Данилом Бернуллі в 1738 р.
Історична довідка
Данило Бернуллі народився 8 лютого 1700 у Гронінгені. Закінчив Базельську гімназію, за настановою батька вивчав медицину. Вчився в Гейдельберзі и Страсбурзі. В 1724 вийшов перший трактат Бернуллі по математиці. С 1725 по 1732 працював в Санкт-Петербурзькій академії наук – спочатку займався фізіологією, потім очолював кафедру математики. В l733 повернувся в Базель, де був професором анатомії і ботаніки, а потім філософії і фізики (з 1750). Внесок Д.Бернуллі в науку важко переоцінити. Разом з М.В. Ломоносовим він стояв біля витоків кінетичної теорії газів. У його працях можна знайти передбачення законів Гей-Люссака, Клайперона і Шарля. Бернуллі був першим, хто висловив думку про те, що тиск газу обумовлене тепловим рухом молекул. У гідродинаміці Д.Бернуллі дав рівняння сталого руху ідеальної нестисливої рідини. Воно виражає собою закон збереження енергії. В 1738 опублікував свою знамениту роботу «Гідродинаміка, або Записки про сили і рухи в рідинах» («Hydrodynamica, sive de viribus et motibus fluidorum commentarii»), у якій сформулював основи механіки рідини. У цьому творі Бернуллі вперше ввів поняття роботи і коефіцієнта корисної дії, записав рівняння стаціонарного руху ідеальної рідини (рівняння Бернуллі), виклав ідеї кінетичної теорії газів. Понад п'ятдесят років (з 1727 по 1778 рр..) Д.Бернуллі займався вивченням коливань. У своїх перших працях він досліджував малі коливання вантажів, підвішених на гнучкої нитки, а також підвішеного важкого однорідного каната. У наступних працях він вивчав коливання струн і стрижнів, ввів поняття простого гармонійного коливання і обгрунтував положення про те, що загальне коливання системи виходить від складання простих гармонійних коливань. Цей важливий принцип отримав згодом назву принципу суперпозиції (накладення) коливань.Значний вклад вніс в математику. Займався розробкою чисельних вирішень алгебраїчних рівнянь, теорією рядів, теорією ймовірностей, дав спосіб вирішення ймовірнісних задач методами математичного аналізі. Був лауреатом почесних премій Паризької академії наук. Був членом Берлінської, Лондонської, Паризької, Санкт-Петербурзької академій наук. Помер Даниїло Бернуллі в Базелі 17 березня 1782.
Динаміка реальної (в'язкої рідини)
Реальна рідина - модель природної рідини, що характеризується ізотропністю всіх фізичних властивостей, але на відміну від ідеальної моделі, володіє внутрішнім тертям при русі.
При вивченні руху реальної (в'язкої рідини) можна піти двома різними шляхами: скористатися готовими диференціальними рівняннями і їхніми рішеннями, отриманими для ідеальної рідини. Облік прояви в'язких властивостей здійснюється за допомогою введення в рівняння додаткових поправочних членів рівняння, вивести нові рівняння для в'язкої рідини. Для практичної інженерної діяльності більш прийнятним слід вважати перший напівемпіричний шлях, другий слід використовувати лише в тих випадках, коли потрібно детальне вивчення процесу руху в'язкої рідини.
Виведення рівняння Бернуллі для елементарної струминки в'язкої рідини
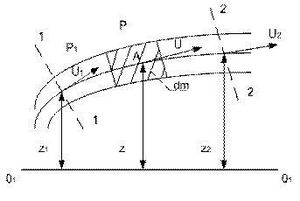
Для виведення рівняння Бернуллі стосовно елементарної цівки в'язкої рідини розглянемо його енергетичний сенс. З цією метою підрахуємо механічну енергію нескінченно малої частки масою dm з центром у т. А, що знаходиться в межах елементарної цівки, щодо горизонтальної площини порівняння О1 – О1.
Як відомо, потенційна енергія дорівнює:
[math]dE_{p}=gdm(z+\frac{p}{\rho g\lambda })[/math]
Кінетична енергія:
[math]dE_{k}=\frac{dmU^{2}}{2}[/math]
Повна механічна енергія складається з суми кінетичної і потенційної енергій:
[math]dE=dE_{p}+dE_{k}=gdm(z+\frac{p}{\rho g\lambda })+\frac{dmU^{2}}{2}[/math]
Віднесемо енергію до одиниці ваги рідини, тобто. визначимо питому енергію
[math]e=\frac{dE}{gdm}=z+\frac{p}{\rho g}+\frac{U^{2}}{2g}[/math]
Таким чином отримаємо вираз, який є рівнянням Бернуллі і виражає закон збереження енергії: вздовж елементарної цівки ідеальної рідини сума потенційної і кінетичної енергії постійна величина, тобто:
[math]z_{1}+\frac{p_{1}}{\rho g}+\frac{U_{1}^{2}}{2g}=z_{2}+\frac{p_{2}}{\rho g}+\frac{U_{2}^{2}}{2g}[/math]
Сума [math]z+\frac{p}{\rho g}[/math] являє собою потенційну енергію, що складається з питомої енергії положення [math]z[/math] і питомої енергії тиску [math]\frac{p}{\rho g}[/math]. Вираз [math]\frac{U^{2}}{2g}[/math] називається питомою кінетичної енергією.
Вздовж елементарної струминки питомі кінетична і потенційна енергії можуть змінюватися, але їхня сума залишається постійною.
При русі в'язкої рідини сумарна питома енергія рідини, яка рухається вздовж струминки, зменшується в силу різних гідравлічних опорів. Отже, для елементарної цівки в'язкої рідини, що знаходиться в сталому русі:
[math]z_{1}+\frac{p_{1}}{\rho g}+\frac{U_{1}^{2}}{2g}\gt z_{2}+\frac{p_{2}}{\rho g}+\frac{U_{2}^{2}}{2g}[/math]
Щоб отримати рівність лівої і правої частини, необхідно в правій частині додати додатковий член [math]hz[/math], що позначає витрату питомої енергії на подолання опорів при русі реальної в'язкої рідини в межах між першим і другим перерізами. У цьому випадку рівняння Бернуллі приймає вигляд:
[math]z_{1}+\frac{p_{1}}{\rho g}+\frac{U_{1}^{2}}{2g}=z_{2}+\frac{p_{2}}{\rho g}+\frac{U_{2}^{2}}{2g}+h_{\sum _{1\rightarrow 2}}[/math]