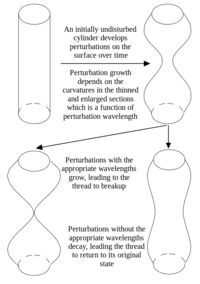
Явище дроблення струминки
Явище дроблення струминки- це процес, у якому маса рідини розбивається у кілька менших мас рідин. Процес характеризується тим, що маса рідини стає тоншою, формує ниткоподібні ділянки між великими вузликами рідини. Ниткоподібні області продовжують ставати тоншими до їх злому, формуючи індивідуальні краплі рідини.
Розпад струминки настає коли дві рідини, або рідина у вакуумі формує вільну поверхню з поверхневою енергією. Якщо є більша площа поверхні, ніж необхідний мінімум для утримання об’єму рідини, система має надлишок поверхневої енергії. Система не при мінімальній енергії буде намагатись перебудовуватись до зниження енергії, що приведе до дроблення рідини у менші маси для мінімізації затрат енергії поверхневих систем, зменшенням поверхневої площі. Точний результат дроблення струминки залежить від поверхневого натягу, в'язкості, щільності і діаметра різьби розпаду, що проходить.
Зміст
Фізичний механізм дроблення струминки
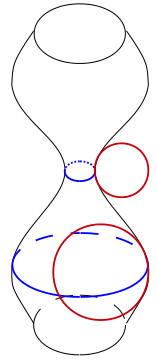
Процес дроблення струминки починається з виробленням невеликих хвилювань на вільній поверхні рідини. Це також відомо як лінійна теорія дроблення струминки. Ці хвилювання завжди присутні і можуть буди сформовані численними джерелами, включаючи вібрації рідинних контейнерів або нерівномірністю у напрузі зсуву на вільній поверхні. В загальному ці коливання приймають довільну форму і тому є складні для точного огляду. Тому корисно взяти перетворення коливань Фур’є щоб розкласти прості коливання у хвилювання різних одиничних довжин хвиль на поверхні струминки. Роблячи це, можна визначити які довжини хвиль коливань будуть з часом зростати, а які – спадати.
Зріст і спадання довжин хвиль може бути визначене перевіркою заряду в тиску, хвилювання довжини хвилі впливає на внутрішню будову струминки рідини. Зміни внутрішнього тиску струминки індукують ся капілярним тиском як вільна від струминних деформацій поверхня. Капілярний тиск залежить від середньої кривизни поверхні розділу в даному місці, тобто тиск залежить від двох радіусів кривизни, які задають форму поверхні. У витонченій частині рідинної струминки проходить розпад, перший радіус кривизни менший ніж радіус кривизни в потовщеній зоні, що призводить до градієнту тиску, що буде, як правило змушувати рідину формувати з тонших ділянок – товщі. Однак, другий радіус кривизни залишається важливим для процесу розвалу.Для деяких довжин хвиль збурень, ефект другого радіуса кривизни може подолати ефект тиску першого радіуса кривизни, викликаючи більший тиск в потовщених областях, ніж в витонченних. Це відштовхне рідину назад в бік тонших областей і дозволить струминці повернутися до вихідного положення у не потурбованій формі. Тим не менш, для інших довжин хвиль збурень, капілярний тиск зменшенний другим радіусом кривизни, що підсилить перший радіус кривизни. Це відвде рідину від тонших до товщих областей і далі сприяти дробленню струмки. Довжина хвилі хвилювання є тому критичним параметром у визначенні, щоб визначити, чи даний струмінь розпадеться у менші маси рідини. Точне математичне дослідження хвиль збурень може привести до співвідношення довжин хвиль, що показують, які є стабільним протягом даного потоку, а також які довжини хвиль збурень будуть зростати найшвидше. Розмір рідинних мас в результати розпаду струминки рідини може бути узгоджена з довжинами хвиль збурення, що ростуть найшвидше.
Нелінійна поведінка
В той час як лінійна теорія корисна для розгляд росту малих коливань на вільній поверхні, коли коливання зростають у певній амплітуді, нелінійні ефекти починають домінувати над поведінкою розпаду. Нелінійна поведінка струминки регулює свій остаточний розпад і в кінцевому підсумку визначає остаточну форму і кількість отриманих мас рідини. Нелінійність вловлюється завдяки використанню само подібності. Самоподібність припускає, що поведінка струменя рідини, поки радіус наближається до нуля, така сама, як поведінка нитки рідини, коли вона має певний кінцевий радіус. Детальне розуміння нелінійної струминки потребує використання асимптотичних розкладань для створення відповідної поведінки масштабування. Численні рішення були знайдені для нелінійної поведінки рідинних струменів на основі сил, які актуальні в конкретних обставина.
Важливі параметри
Як струминка піддається розриву, регулюється кількома параметрами, серед яких є число Рейнольдса, число Вебера і довжина хвилі хвилювання. Хоча ці цифри є спільними в механіці рідин, обрані в якості мір параметри, повинні відповідати розпаду струминки. Тим не менш, ці міри можуть змінюватися залежно від характеристик розглянутих проблем. Число Рейнольдса являє собою співвідношення між інерцією і вузькими ефектами в потоці. Для великих чисел Рейнольдса, ефекти руху нитки набагато значніші, ніж в’язке розсіювання. В’язкість тільки має мінімальне демпфірування впливу на нитку. Для малих чисел Рейнольдса, в’язка дисипація велика і будь які коливання швидко згладжуються зі струминки. Число Вебера – це співвідношення між інерційним і поверхневим ефектом натягу в струмині. Коли число Вебера велике, інерція нитки велика, що супротивляться тенденції поверхневого натягу для того, щоб згладити вигнуті поверхні. Для низьких чисел Вебера, зміни капілярного тиску через коливання поверхні значні і тиск поверхні домінує над поведінкою струмини.
Лінійна стабільність нев’язких рідин
Плато вважав струминку рідини стабільною лише коли інерційні і поверхневі ефекти натягу були наявні. За розкладання довільного коливання на вільні поверхні до їх довжин хвиль, він зміг вивести умову стабільності струменя в умовах коливання:
Де ω – зростання коливання, σ – поверхневий натяг рідини, k є число коливань, ρ – щільність рідини, а є початковий радіус незбудженої рідини і І – модифікована функція Бесселя першого виду. За обчисленням швидкості росту залежно від хвильового числа, можна визначити, що найбільш зростаючі коливання відбуваються при:
Довжина хвилі максимальної нестійкості зростає при зростанні радіуса різьблення. Важливо, нестабільні режимі можливі лише при:
