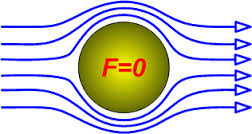
Парадокс Даламбера

Парадокс Даламбера - ствердження в гідродинаміці ідеальної рідини, згідно якому при стаціонарному (не обов'язково потенційному і нерозривному ) обтіканні твердого тіла безмежним поступальним потоком нев'язкої рідини, при умові вирівнювання параметрів далеко попереду і позаду тіла, сила опору дорівнює нулю.

Рис.1 Парадокс Даламбера‎

Варіанти назв парадоксу

Разом із назвою парадокс Даламбера в науковій літературі зустрічаються наступні назви: парадокс Даламбера-Ейлера, Ейлера-Даламбера, і парадокс Ейлера.

Історична довідка

Зоммерфельд із посиланням на Озеєна згадує Спінозу як раннього дослідника парадоксу. Скоріш за все мова йшла про роботу "Основи філософії Декарта, доведені геометричним способом", в якій Спіноза аналізує умови, при яких: "тіло ,наприклад, наша рука, могла б рухатися в будь-якому напрямку, не протидіючи і не відчуваючи впливу інших тіл". В окремому випадку, обтікання тіла симетричного відносно поперечної площини, Даламбером було виявлено перетворення опору в нуль. Термін "парадокс" вперше було застосовано в 1786 році Даламбером для характеристики перетворення опору в нуль.

Різні варіанти парадоксу Даламбера

У силу принципу відносності Галілея можна говорити і про парадокс Даламбера у разі поступального прямолінійного руху тіла з постійною швидкістю в безмежному об'ємі ідеальної рідини.

Крім цього, цей парадокс справедливий при обтіканні тіла потоком, вкладеним в нескінчений циліндричний канал.

Особливості формулювання парадоксу

Важливо відмітити, що в формулюванні парадоксу йде мова лише про відсутність складової сили, діючої на тіло яке паралельне потоку на безкінечності. Складова сили, яка перпендикулярна до потоку (підйомна сила), може бути відмінна від нуля навіть при виконанні всіх умов парадоксу. Слід звернути увагу на те, що момент сил, діючих на тіло зі сторони потоку, може бути відмінний від нуля. Так при нерозривному обтіканні нахиленої до потоку пластинки навіть при нульовій циркуляції швидкості виникає момент сил, прагнучий повернути пластинку поперек потоку. При наявності об'ємних сил (сили тяжіння) зі сторони рідини на тіло може діяти Архімедова сила, проте її не можна рахувати складовою сили опору, так як вона не перетворюється в нуль в рідині, яка знаходиться в стані спокою.

Випадки порушення парадоксу

Добре відомо, що при обтіканні тіла реальним потоком рідини завжди присутня сила опору, наявність якої пояснюється порушенням певних умов:

• якщо рідина не є ідеальною, може виникати сила опору, зв'язана з дією в'язкого тертя;
• якщо рух тіла в рідині не є стаціонарним, то навіть у нев'язкої рідини виникає сила опору інерційної природи;
• якщо течія не неперервна, то параметри потоку далеко попереду і позаду тіла не можуть співпадати, що призводить до виникнення опору;
• якщо рідина не займає весь простір навколо тіла, то парадокс теж може порушуватись;
• якщо параметри потоку далеко попереду і позаду тіла не вирівнюються, то сила опору теж відмінна від нуля;

Експерементальні результати

Якщо створити умови, в яких обтікання тіла буде доволі близьким до умов в формулюванні парадоксу, наприклад, якщо надати тілу форму яка легко обтікається, можна досягти зменшення опору в порівнянні із формами, які важко обікаються, в десятки і сотні разів . При русі частинок в твердих тілах відомий ефект "надглибокого проникнення ". Одне із пояснень цього ефекту - якісно аналогічне парадоксу Даламбера: зменшення опору досягається за рахунок того, що при певних умовах, вплив частинки на зовнішнє середовище зменешений.

Література

• Grimberg G., Pauls W., Frisch U. Genesis of d'Alembert's paradox and analytical elaboration of the drag problem // Physica D. — 2008. — Т. 237.

Посилання

• Парадокс Д'Аламбера — статья из Большой советской энциклопедии

Примітки

• «При доказательстве парадокса Даламбера, вообще говоря, не предполагается, что движение жидкости потенциально и что в жидкости нет конечных полостей, заполненных газом, паром или жидкостью» (Седов Л. И. Механика сплошной среды. — М.: Наука, 1970. — Т. 2. — С. 74. — 568 с.).
• ↑ Чёрный Г. Г. Газовая динамика. — М.: Наука, 1988. — С. 118-120. — 424 с. — ISBN 5-02-013814-2.
• ↑ «Если бы каверна имела конечную длину, то на основании известного свойства установившегося безвихревого движения <…> сила сопротивления, действующая со стороны жидкости на тело вместе с каверной, была бы равна нулю и, следовательно, была бы равна нулю и сила сопротивления, действующая на тело» (Бэтчелор Дж. Введение в динамику жидкости / Пер. с англ. под ред. Г.Ю.Степанова. — М.: Мир, 1973. — С. 614. — 760 с.).
• Седов, с. 71.
• ↑ Чёрный, с. 120.
• ↑ Кочин Н. Е., Кибель И. А., Розе Н. В. Теоретическая гидромеханика. — М.: Физматгиз, 1963. — Т. 1. — 584 с.
• ↑ Чаплыгин С. А. Результаты теоретических исследований о движении аэропланов // Избранные труды. Механика жидкости и газа. Математика. Общая механика. — М.: Наука, 1976. — С. 131-141.
• ↑ Зоммерфельд А. Механика деформируемых сред / Пер. с нем. Е.М.Лифшица. — М.: ИЛ, 1954. — С. 264. — 488 с.
• ↑ Спиноза Б. Избранные произведения в двух томах / Общая ред. и вступ. статья В.В.Соколова. — М.: Политиздат, 1957. — Т. 1. — С. 256. — 632 с.
• ↑ Пункт 247 и рис. 77 в книге: D’Alembert. Traité de l'équilibre et du mouvement des fluides. — 1744.
• ↑ Эйлер Л. Новые основания артиллерии // Ред. Б. Н. Окунев Исследования по баллистике. — М.: Физматлит, 1961. — С. 7-452.
• ↑ D’Alembert Paradoxe proposé aux Géomètres sur la résistance des fluides // Opuscules mathématiques. — Paris, 1768. — Т. 5. — С. 132-138.
• ↑ Козорезов К.И., Максименко В.Н., Ушеренко С.М. Исследование эффектов взаимодействия дискретных микрочастиц с твердым телом // Избранные вопросы современной механики. — М.: Изд-во Моск. ун-та, 1981. — С. 115-119.
• ↑ Григорян С.С. О природе «сверхглубокого» проникания твердых микрочастиц в твердые материалы // ДАН СССР. — 1987. — Т. 292, № 6. — С. 1319-1323.
• ↑ Чёрный Г.Г. Механизм аномально низкого сопротивления при движении тел в твердых средах // ДАН СССР. — 1987. — Т. 292, № 6. — С. 1324-1328.
• ↑ Киселев С.П., Киселев В.П. О механизме сверхглубокого проникания частиц в металлическую преграду // ПМТФ. — 2000. — Т. 41, № 2. — С. 37-46.