Закон Беца
Альберт Бец (25 грудня 1885 Швайнфурт - 16 квітня 1968 Геттінген), був німецький фізик і піонер технології вітряного двигуна.
Закон Беца
Закон Беца (англ. Betz' law) — визначає максимальну енергію, яку можна отримати від «гідравлічного вітрового рушія», або вітрової турбіни. Закон Беца було відкрито 1919 року німецьким фізиком Альбертом Бецом.Закон отриманий з принципів збереження маси і імпульсу повітряного потоку, поточного через ідеалізований «диск приводу головок», який витягає енергію з потоку вітру. Відповідно до закону Беца, ніяка турбіна не може захопити більше, ніж 16/27 (59,3%) кінетичної енергії на вітрі. Фактор 16/27 (0.593) відомий як коефіцієнт Беца. Практичні вітряні двигуни сервісного масштабу досягають в пікових 75% до 80% межі Беца.
Пояснення
Закон Беца встановлює, що вітряна турбіна ніколи не може мати ККД більше, ніж 59.259%. Цей закон ґрунтується на тому, що якщо вся енергія, що надходить від руху повітря в турбіні, буде перетворена в корисну енергію, то швидкість повітря за турбіною дорівнюватиме нулю. Але, якщо повітря зупинилось на виході з турбіни, то також має припинитись потік повітря через турбіну. Для того, щоб повітря продовжував рухатися крізь турбіну і віддавав енергію, необхідно відводити повітря за турбіною. Різниця між кінетичною енергією повітря перед турбіною та енергією на відведення повітря за турбіною якраз і становить обчислене значення — 59,259%.
Доказ
Межа Беца показує максимально можливу енергію, яка може бути отримана за допомогою дискового привода від текучого середовища, що протікає з певною швидкістю.
Припущення
1.Ротор не володіє центром, це - ідеальний ротор з нескінченним числом лопатей, у яких немає опору. Будь-який опір лише понизив бицю ідеалізовану вартість.
2.Потік нестисливий. Щільність залишається постійною, і немає ніякої теплопередачі.
3.Єдина тяга на всій площі диска або ротора.
Застосування збереження маси (рівняння нерозривності)
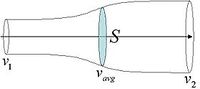
Застосовуючи збереження маси для цього контрольного об'єму, масова витрата (маса рідини, що протікає в одиницю часу) визначається за формулою:
[math]m = \rho {A_1}{v_1} = \rho Sv = \rho {A_2}{v_2}[/math]
де v1 - швидкість в передній частині ротора v2 - швидкість на виході з ротора, V - швидкість пристрою живлення рідини. ρ - являє собою щільність рідини, S - площа турбіни. A1 і A2 - площа рідини до і після досягнення турбіну.
Так щільність площі і швидкість повинні бути рівні в кожній з трьох областей: до, під час проходження через турбіну і після нього. Сила, що діє на рух ротора може бути записана у вигляді:
[math]F = ma = m\frac{{dv}}{{dt}} = m\Delta v = \rho Sv({v_1} - {v_2})[/math]
Сила і робота
Робота, зроблена силою, може бути написана з приростом як:
[math]dE = F \cdot dx[/math]
і сила вітру є:
[math]P = \frac{{dE}}{{dt}} = F \cdot \frac{{dx}}{{dt}} = F \cdot v[/math]
Тепер заміна силою F вирахованій вище в рівнянні силі призводить до сили витягнутої з вітру:
[math]P = \rho \cdot S \cdot {v^2} \cdot ({v_1} - {v_2})[/math]
Однак сила може бути обчислена інакше, за допомогою кінетичної енергії. Застосування рівняння збереження енергії.
[math]P = \frac{{\Delta E}}{{\Delta t}} = \frac{1}{2} \cdot m \cdot (v_1^2 - v_2^2)[/math]
Озираючись на рівняння нерозривності, заміна для масової витрати дає наступне:
[math]P = \frac{1}{2} \cdot \rho \cdot S \cdot v \cdot (v_1^2 - v_2^2)[/math]
Обидва з цих виразів для сили повністю діють, один був отриманий дослідивши зростаючу зроблену роботи, а інший по збереженню енергії. Прирівнявши ці два вирази отримаємо:
[math]P = \frac{1}{2} \cdot \rho \cdot S \cdot v \cdot (v_1^2 - v_2^2) = \rho \cdot S \cdot {v^2} \cdot ({v_1} - {v_2})[/math]
Розглядаючи два прирівняних вираження отримуємо цікавий результат, а саме:
[math]\frac{1}{2} \cdot (v_1^2 \cdot v_2^2) = \frac{1}{2} \cdot ({v_1} - {v_2}) \cdot ({v_1} + {v_2}) = v \cdot ({v_1} - {v_2})[/math]
або
[math]v = \frac{1}{2} \cdot ({v_1} + {v_2})[/math]
Таким чином, швидкість вітру на роторі може бути прийнятий в якості середнього значення на вході і виході швидкостей. (Це можливо сама парадоксальна стадія походження закону Беца).
Математичне обгрунтування
Відповідно до закону збереження енергії, кінетична енергія турбіни має становити:[math]E = \frac{1}{2}m(v_1^2 - v_2^2) = \frac{1}{2}\rho Sv(v_1^2 - v_2^2) = \frac{1}{4}\rho S({v_1} + {v_2})(v_1^2 - v_2^2) = \frac{1}{4}\rho Sv_1^3\left( {(1 - {{\left( {\frac{{{v_2}}}{{{v_1}}}} \right)}^2} + \left( {\frac{{{v_2}}}{{{v_1}}}} \right) - {{\left( {\frac{{{v_2}}}{{{v_1}}}} \right)}^2} - {{\left( {\frac{{{v_2}}}{{{v_1}}}} \right)}^3}} \right)[/math]
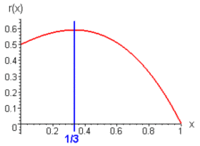
де: E — енергія турбіни, m — маса повітря, що проходить крізь турбіну, ρ — питома вага; [math]{v_1},{v_2}[/math] — швидкість на вході і виході відповідно. Диференціювання рівняння за змінною [math]v = \frac{{{v_2}}}{{{v_1}}}[/math] дозволяє віднайти максимум енергії при співвідношенні [math]v = \frac{{{v_2}}}{{{v_1}}} = \frac{1}{3}[/math] . Відповідно, отримана енергія буде становити:
[math]{P_{\max }} = \frac{{16}}{{27}} \cdot \frac{1}{2} \cdot \rho \cdot S \cdot v_1^3[/math]
Сила отримана з циліндра рідини з площею поперечного перерізу S і швидкістю [math]{v_1}[/math] є:
[math]P = {C_p}\frac{1}{2} \cdot \rho \cdot S \cdot v_1^3[/math]
Довідкова сила для обчислення ефективності Бец - сила в рухомої рідини в циліндрі із взаємною площею поперечного перерізу S і швидкістю [math]{v_1}[/math].
[math]{P_{wind}} = \frac{1}{2} \cdot \rho \cdot S \cdot v_1^3[/math]
У «коефіцієнта сили» С (= Р / Р) є максимальне значення: С = 16/27 = 0,593 (або 59,3%; однак, коефіцієнти роботи зазвичай виражаються як десяткове число, не у відсотках).