Жан-Шарль Борда
Жан-Шарль, де Борда (4 травня, 1733 - 19 лютого, 1799) - французький математик, фізик, політолог і моряк.
Зміст
Біографія
Народився в місті Дакс, на південному-заході Франції. Він навчався в знаменитому коледжі Генріха Великого (Henri IV) в Ла-Флеш (La Flèche), на основі якого згодом було відкрито Національне Військове Училище (Prytanée National Militaire). Спочатку випускник престижного навчального закладу збирався зайнятися математикою, але його батьки наполягли на військовій кар'єрі. Він зайнявся військовим будівництвом, після чого перейшов у легку кавалерію. В 1756р. він написав "Доповідь про рух снарядів" («Memoire sur le mouvement des projectiles»), результат його роботи як військового інженера. За це в 1764р. його було обрано в Французьку академію наук.
Борда був моряком і науковцем, він проводив час в Карибському Морі, випробовуючи нововинайдення в хронометрах. В 1777-1978 роках він брав участь в Американській Війні за Назалежність. В 1781 році він керував кількома кораблями на Французькому Флоті. В 1782 він був затриманий англійцями, але невдовзі повернувся до Франції. Він повернувся на Французький Флот в якості інженера і займався вдосконаленням водних коліс та помп. В 1784 він був призначеним Інспектором Франції в Військовому Кораблебудуванні, і з допомогою військово-морського архітектора Жака Сане в 1786р. представив вагому будівельну програму по відновленню французького військового флоту, що базувалася на розробках Сане.
В 1770р. Борда розробив впорядковану преференційну систему голосування, що відома як "система підрахунку Борда". Французька Академія Наук використовувала метод Борда при виборах своїх членів протягом понад двох десятиліть, поки система не була відмінена Наполеоном Бонапартом, який, ставши президентом Академії в 1801р., наполягав на використанні свого власного методу. Система підрахунку Бора сьогодні використовується в деяких академічних закладах, на змаганнях, та в деяких політичних юрисдикціях.
В 1778р. він опублікував свій метод визначення Кутової Відстані (Відстані від Землі до Місяця) для розрахунку довготи, який був найкращим з кількох подібних математичних методик для навігації і визначення місцезнаходження в часи, коли не використовувалися хронометри; і який використовувався, наприклад, Льюісом і Кларком, щоб виміряти довготу і широту при дослідженні північного заходу Сполучених Штатів.
Ще одним його внеском є розробка стандартного метра, основи метричної системи у відповідності до вимірів Деламбре.
Як розробник пристрою, він вдосконалив рефлективний круг (винайдений Тобіасом Мейєром) і повторюваний круг (винайдений з його допомогою Етьєном Ленором), що пізніше використовувались Деламбре та Механом при вимірах дуги меридіана від Дюнкерка до Барселони.
Таблиці логарифмів
З винайденням метричної системи після Французької Революції було вирішено, що чверть круга буде поділено на 100 градусів замість 90 градусів, а градус - на 100 секунд замість 60 секунд. Це вимагало розрахунку тригонометричних таблиць та логарифмів відповідно до нового розміру градуса та інструментів виміру кутів в новій системі.
Борда розробив пристрій для виміру кутів в нових одиницях (пристрій не міг більше називатися «секстант»), який пізніше використовувався Деламбре для виміру меридіанів між Дюнкерком та Барселоною, щоб визначити довжину метра. Таблиці логарифмів синусів, секансів і тангенсів були необхідними для мореплавства. Борда був ентузіастом у винайденні метричної системи і розробляв таблиці цих логарифмів з 1792 року, але їх публікація відкладалася до його смерті, в 1801 вони були опубліковані як Таблиці Логарифмів синусів, секансів, тангенсів, косекансів, косинусів і котангенсів для чверті круга, що поділена на 100 градусів, де градус поділено на 100 мінут , а мінута - на 100 секунд і на 10 десятих, і включаючи його таблиці логарифмів, на 7 десятих з 10 000 до 100 000 з таблицями, що містять результати на 10 десятих.
Розподіл градуса на соті супроводжувався розподілом дня на 10 годин, що складалися зі 100 хвилин і карти повинні були вказувати нові градуси довготи та широти. Республіканський Календар був анульований Наполеоном в 1906 році, а разом з ним, очевидно, і круг із 400 градусами.
Рефлективний круг
Рефлективний круг було винайдене в 1752р. німецьким геометром і астрономом Тобі асом Мейєром, а в деталях опубліковане в 1767р. Його розробці передував секстант, а мотивацією розробки була потреба створити кращий пристрій для спостереження.
Рефлективний круг - це повністю круглий пристрій, поділений на 720 градусів (щоб виміряти відстань між небесними тілами, нема необхідності читати кут, більший за 180 градусів, оскільки мінімальна відстань завжди буде менша 180 градусів). Мейєр представив детальний опис цього приладу Колегії Довготи і Джон Берд використав цю інформацію, щоб побудувати прилад в 16 дюймів в діаметрі для оцінювання Королівським Флотом. Цей прилад був одним з тих, які використовував адмірал Джон Кампбелл під час оцінки методу Місячної Відстані. Прилад відрізнявся тим, що був поділений на 360 градусів і був таким важким, що був обладнаний опорою, приєднаною ременем. Прилад не було визнано кращим за октант Хадлі, він був менш зручним у використанні. В результаті, Кампбелл рекомендував конструкцію секстанта.
Борда далі розробляв рефлективні круги. Він змінив положення телескопічного вічка таким чином, що можна було використовувати дзеркало для отримання зображення з будь-якого боку від телескопа. Це виключило необхідність перевіряти, що при читанні нуля, дзеркала розміщені точно паралельно. Це спростило використання приладу. Подальші вдосконалення були зроблені з допомогою Етьєна Ленора. В 1777 вони обидва вдосконалили прилад до його кінцевого вигляду. Цей прилад був таким особливим, що його назвали кругом Борда.
Джозеф де Мендоза переробив рефлективний круг Борда (Лондон, 1801р). Метою було його використання в поєднанні з Місячними Таблицями, опублікованими Королівським Науковим Товариством (Лондон, 1805). Він розробив прилад з двома концентричними кругами і верньєрною шкалою, і для виключення помилки рекомендував в середньому три зчитування. Система Борда була основана на крузі не з 360, а з 400 градусів (Борда роками обчислював свої таблиці для круга, поділеного на 400 градусів). Місячні Таблиці Мендози використовувалися протягом майже всього 19-го століття.
Едвард Троутон також змінив рефлективний круг. Він створив дизайн з трьома вказівними стрілками і верньєрами. Це забезпечувало три одночасних зчитування для зменшення імовірності помилки.
Як пристрій навігації, рефлективний круг було більш поширеним на французькому флоті, ніж на англійському.
Одним з пристроїв, що походить від рефлективного круга, є повторюваний круг. Винайдений Ленором в 1784 р. пристрій Борда і Ленор вдосконалювали як прилад для геодезичного огляду. Оскільки він не використовувався для астрономічних вимірів, в ньому не використовувалося подвійне відображення і були замінені два телескопічні вічка. Відтак, це не був рефлективний прилад. Він був вагомим, будучи рівним чудовому теодоліту, створеному знаменитим розробником приладів Жессе Рамстеном.
Повторюваний круг
Повторюваний круг - це пристрій для геодезичного спостереження, винайдений Етьєном Тенором в 1784р., коли він був асистентом Борди, який пізніше вдосконалив цей пристрій. Він був вагомим, будучи рівним чудовому теодоліту, створеному знаменитим розробником приладів Жессе Рамстеном. Він використався Деламбре та Механом при вимірах дуги меридіана від Дюнкерка до Барселони.
Повторюваний круг зроблений з двох телескопів, розміщених на спільній осі зі шкалою для виміру кута між ними. Прилад поєднує множинні виміри, щоб збільшити точність потрібно виконати наступну послідовність дій :
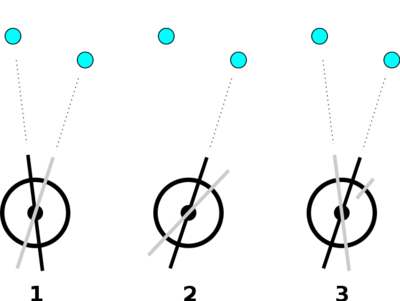
На цьому етапі, кут на приладі є вдвічі більшим за кут значимості між точками. При повторенні процедури інструмент показує 4х значимості кута з подальшим зростанням його до 6х, 8х і так далі. Таким чином, можна додати багато вимірів, що дозволяє виключити випадкові помилки при вимірах.
Формула Борда-Карно
У 1766 році Борд вивів формулу для втрат при раптовому розширенні,яку назвали у його честь. Формула (теорема) Борда-Карно — у гідродинаміці це емпірична формула, що описує втрати механічної енергії рідини у зв'язку із раптовим розширенням потоку. Вона описує, як знижується повний напір у зв'язку із втратами. Це рівняння, на відміну від рівняння Бернуллі для ідеальної рідини, де загальна питома енергія рідини стала уздовж лінії течії дозволяє розрахувати втрати на місцевому гідравлічному опорі. Це рівняння назване на честь Жана-Шарля де Борда (Jean-Charles de Borda) (1733–1799) та Лазара Карно (Lazare Nicolas Marguerite Carnot) (1753–1823).
Формула:
ΔE — втрата механічної енергії рідиною;
ξ — емпіричний безрозмірний коефіцієнт втрат, що набуває величину між нулем і одиницею, 0 ≤ ξ ≤ 1;
ρ — густина рідини;
V1 і V2 — середня швидкість потоку перед і за раптовим розширенням відповідно.
У випадку раптового розширення коефіцієнт втрат дорівнює одиниці. В інших випадках, коефіцієнт втрат повинен бути визначений за допомогою інших засобів, найчастіше з використанням емпіричної формули (на основі даних, отриманих дослідним шляхом). Формула Брода-Карно для розрахунку втрат енергії справедлива для випадку зменшення швидкості,V 1 >V2, в іншому випадку втрати ΔE прямують до нуля (без додаткової механічної роботи сил тертя).
Публікації
- Книга "Опис і використання повторюваного круга".1778р.
- "Доповідь про рух снарядів" (Mémoire sur le mouvement des projectiles).1756р.
Відзнаки
- П'ять французьких кораблів були названі в його честь.
- Відкритий в 1997 році астероїд номер 175726 носить ім'я Борда.
- Обсерваторія в його рідному місті Дакс названа в його честь.
- Його ім'я в числі 72 імен великих французьких учених було написано на Ейфелевій вежі (Tour Eiffel)




