Інтеграл Бернуллі

Даниїл Бернуллі

Інтегра́л Берну́ллі - рівняння гідродинаміки, що визначає в кожній точці потоку ідеальної рідини або баротропного газу взаємозв'язок між тиском [math]p[/math], що встановився, ([math]p=F(\rho)[/math]) швидкістю [math]\vec v[/math] потоку у відповідній точці та силовою функцією [math]\vec u(x,y,z)[/math] об'ємних сил.

Історична довідка

Д.Бернуллі народився 29 січня 1700р. в Гронінгені (Голландія), де його батько викладав математику в університеті

Внесок Д.Бернуллі в науку важко переоцінити. Разом з М.В. Ломоносовим він стояв біля витоків кінетичної теорії газів. У його працях можна знайти передбачення законів Гей-Люссака, Клайперона і Шарля. Бернуллі був першим, хто висловив думку про те, що тиск газу обумовлене тепловим рухом молекул. У гідродинаміці Д.Бернуллі дав рівняння сталого руху ідеальної нестисливої ​​рідини. Воно виражає собою закон збереження енергії. Рівняння Бернуллі дозволяє зрозуміти багато явищ гідромеханіки і аеромеханіки. Воно використовується при розрахунку різних трубопроводів, насосів і витратомірів, дослідженні процесів фільтрації і т.п. Разом з деякими іншими співвідношеннями рівняння Бернуллі, записане для середовища зі змінною густиною "РВ", складає основу газової динаміки. Д. Бернуллі спільно з Л. Ейлером належить головна заслуга у розробці механіки рідких тіл. Понад п'ятдесят років (з 1727 по 1778 рр..) Д.Бернуллі займався вивченням коливань. У своїх перших працях він досліджував малі коливання вантажів, підвішених на гнучкої нитки, а також підвішеного важкого однорідного каната. У наступних працях він вивчав коливання струн і стрижнів, ввів поняття простого гармонійного коливання і обгрунтував положення про те, що загальне коливання системи виходить від складання простих гармонійних коливань. Цей важливий принцип отримав згодом назву принципу суперпозиції (накладення) коливань. Данила Бернуллі разом з Д'Аламбером, Л. Ейлером і Лагранжем можна вважати засновником математичної фізики. Також Д.Бернуллі ввів термін «гідродинаміка» для того, щоб об'єднати дві науки: гідростатику і гідравліку. Д. Бернуллі відкрив теорему, відому під його іменем. Це так звана загальна теорема усталеного течії, з якою закон Торрічеллі виходить як наслідок. Під сталим течією (mouvement permanent) мається на увазі такий рух рідини, при якому в кожній точці простору, займаного рідиною, величини і напрямки швидкостей точок рідини і величина тиску не змінюються з плином часу. При такому рухcі всі ці точки рідини, які послідовно проходять через одну і ту ж точку простору, рухаються одна за одною по одній і тій же траєкторії; кожну таку траєкторію можна назвати лінією струму. Якщо взяти майданчик малих розмірів, нормальну до траєкторії і через всі точки контуру майданчика провести лінії струму, то вони утворюють поверхню, усередині якої буде полягати деяка струмінь поточної рідини, поперечні перерізи якої, взагалі кажучи, будуть неоднакові в різних місцях. У 1738 році Даніель Бернуллі відкрив закон, на якому після і почалося базуватися літакобудування. І за його принципом вже у дев'ятнадцятому столітті багато людей, що почали займатися повітроплаванням, почали використовувати при створенні планерів. Джордж Кейлі, якого зараз називають «батьком аероплана», в 1853 році збудував і вдало випробував перший у світі планер. Який далі був модернізований до керованого. У 1738 році світу був представлений новий інтеграл,який взяв свою назву,згідно із його першовідкривачем Інтеграл Бернуллі

Інтеграл Бернуллі для елементарної струминки стислової рідини або газу

Рівняння Ейлера можуть бути використані для опису руху газів.У цьому випадку масовими силами можна знехтувати ,і рівняння Ейлера набудуть вигляду :

[math]-\frac{1}{\rho }\frac{\mathrm{d} p}{\mathrm{d} x}=\frac{\partial u_{x}}{\partial t}[/math]

[math]-\frac{1}{\rho }\frac{\mathrm{d} p}{\mathrm{d} y}=\frac{\mathrm{d} u_{y}}{\mathrm{d} t}[/math]

[math]-\frac{1}{\rho }\frac{\mathrm{d} p}{\mathrm{d} z}=\frac{\mathrm{d} u_{z}}{\mathrm{d} t}[/math]

Наведену систему рівнянь перетворимо,звівши її до одного.Для цього ліву і праву частину кожного з рівнянь помножимо відповідно на [math]{\mathrm{d} x} , {\mathrm{d} y} ,{\mathrm{d} z}[/math] і складемо ліві та праві частини усіх трьох рівнянь:

[math]-\frac{1}{\rho }(\frac{\mathrm{d} p}{\mathrm{d} x}{\mathrm{d} x}+\frac{\mathrm{d} p}{\mathrm{d} y}{\mathrm{d} y}+\frac{\mathrm{d} p}{\mathrm{d} z}{\mathrm{d} z})=\frac{\mathrm{d} u_{x}}{\mathrm{d} t}{\mathrm{d} x}+\frac{\mathrm{d} u_{y}}{\mathrm{d} t}{\mathrm{d} y}+\frac{\mathrm{d} u_{z}}{\mathrm{d} z}{\mathrm{d} z}[/math]

Оскільки : [math]{\mathrm{d} x}=u_{x}dt,dy=u_{y}dt,dz=u_{z}dt[/math] то маємо :

[math]-\frac{1}{\rho }dp=u_{x}du_{x}+u_{y}du_{y}+u_{z}du_{z}[/math]

АБО

[math]\frac{dp}{\rho }+d(\frac{u^{2}}{2})=0[/math] (9.14)

Інтегруємо рівняння (9.14)

[math]\int \frac{\mathrm{d} p}{ \rho }+\frac{u^{2}}{2}=const[/math] (9.15)

Рівняння (9.15)називають інтегралом Бернуллі для елементарної струминки стислової рідини або газу

Для випадку адіабатичної течії газу

[math]\frac{p}{\rho ^{k}}=C[/math] чи [math]p=C\rho ^{k}[/math] (9.16)

де k - показник адіабати.

Диференціал тиску

[math]dp=Ck\rho ^{k-1}dp[/math]

і тоді

[math]\int \frac{\mathrm{d} p}{\mathrm{d} \rho }=Ck\int \rho ^{k-2}d\rho =C\frac{k}{k-1}\rho ^{k-1}+const[/math]

а з урахуванням (9.16)

[math]\int \frac{\mathrm{d} p}{ \rho }=\frac{k}{k-1}\frac{p}{\rho }+const[/math]

Таким чином,інтеграл Бернулліматиме таку форму запису:

[math]\frac{k}{k-1}\frac{p}{\rho }+\frac{u^{2}}{2}=const.[/math] (9.17)

Одережане рівняння для ідеального газу використовують в суакупності з рівняннями нерозривності та термодинамічного процесу.Постійну інтегрування можна виразити через параметри газу у стані спокою.Вцьому випадку [math]u=0,p=p_{0},\rho =\rho _{0},[/math] Тоді стала інтегрування

[math]const=\frac{k}{k-1}\frac{p_{0}}{\rho _{0}}[/math]

Інтеграл Бернуллі у загальному вигляді,з урахуванням стиску газу

Витоки даного рівняння безпосередньо виходять від рівняння Ейлора,відповідно [math]\rho \frac{\mathrm{d} w}{\mathrm{d} t}=\rho F-Rp[/math],де Rp градієнт тиску . Це рівняння має назву - рівняння ідеальної рідини. Інший його вигляд:

[math]\rho \left ( \frac{\mathrm{d} w}{\mathrm{d} t}+V\cdot R\cdot V \right )=\rho \cdot F-R\cdot p[/math] цю конєктивну частину заміняємо за відомою формолою векторного аналізу : [math]\rho \left ( \frac{\partial w}{\partial t}+R\left [ V^{2}/2 \right ]+rot V\cdot U \right )=\rho F-Rp[/math].

Коли ми говоримо,що ідеальна рідина/газ,то [math]\mu[/math] (коофіцієнт в'язкості)=0 і [math]\lambda[/math] (кооф.провідності)=0 теж!це так зване визначення для ідеальної рідини/газу.

Якщо вважати,що рух вимірювального елемента - стаціонарний ([math]\frac{V}{\partial t}=0[/math]) і зовнішні сили мають потенціал ([math]F=\sigma U[/math]),тоді при наступних умовах поділивши на р матимемо :

[math]R\left ( \frac{V^{2}}{2}+p+U \right )=-\left ( rotV\cdot U \right )=-{\partial U}\cdot V[/math],тому що ([math]W=\frac{1}{2}\cdot rotV[/math]) (W - кутова швидкість).

Ми ввели функцію p-для якої є свій інтеграл: [math]p=\int \frac{\partial p}{\rho }[/math] слід зауважити,що траєкторія руху рідини співпадає із лінією потоку і крім [math]\mu =0,\frac{V}{\partial t}=0,F={\partial U}[/math] введемо 4 поняття p=p(g) функція від щільності є [math]\gamma[/math] .

[math]p=\int \frac{\partial p}{\rho \left ( p,\gamma \right )}[/math] функція тиску.Тепер ми бачемо,що права частина =0,маємо :

[math]\frac{\mathrm{d} V}{\mathrm{d} t}(\frac{V^{2}}{2}+p+u)=0[/math]

звітси маємо : [math]\frac{V^{2}}{2}+p+U=H\left ( \gamma \right )=const\left ( \gamma \right )[/math].

Якщо проінтегрувати функцію тиску,то отримаємо інтеграл Бернуллі.

Кінцевий вигляд інтегралу

[math]\int \frac{dp}{\rho}\ = C - \frac{1}{2}\left | \vec v^2 \right | + \vec u[/math]
Стала [math]C[/math] має для кожної лінії струменю своє значення, що змінюється з переходом від одної лінії струменю до іншої. Якщо рух потенційний, то стала [math]C[/math] одна і таж для всього потоку.
Для руху, що не встановився, інтеграл Бернулі (називають інколи інтегралом Коші—Лагранжа) має місце за наявності потенціалу швидкостей:
[math]\int \frac{dp}{\rho}\ = \frac{\partial \phi}{ \partial t} - \frac{1}{2}\left | \vec v^2 \right | + \vec u + f(t)[/math],
причому [math]\mathbf{v} = \text{grad}\, \phi(x,y,z,t)[/math] а [math]f(t)[/math] — довільна функція часу.
Для нестискуваних рідин ліва частина рівнянь приводиться до вигляду [math]\frac{p}{\rho}[/math] для баротропного газу ([math]p=F(\rho)[/math]) — до вигляду:
[math]\int \frac{dp}{\rho}\ = \int F'(\rho) \frac{d \rho}{\rho}\[/math]

Практичне застосування

Інтеграл безпосередньо застосовується і використовується в аеро- і гідродинаміці – співвідношення, що зв’язує газо- або гідродинамічні змінні уздовж лінії струму сталого баротропного плину ідеальної рідини або газу в потенційному полі масових сил.Гідроаеромеханіки - наука про рух і рівновагу рідин і газів.

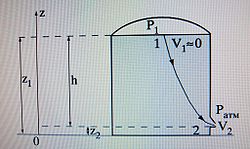
Як приклад використання інтеграла Бернуллі можна визначити швидкість витікання нестисливої ​​рідини з посудини (рис. 5). У разі закінчення рідини з цієї посудини рівень рідини знижується, тобто швидкість поверхні рідини, взагалі кажучи, відмінна від нуля. Однак при досить широкій посудині з вузьким отвором витікання можна прийняти, що V1 = 0. Оскільки по всій поверхні рідини в посудині тиск р1 = const, то постійна уздовж лінії струму на всіх лініях струму буде однаковою. Інтеграл Бернуллі вздовж якої-небудь лінії струму, наприклад, що з'єднує точки 1 (на поверхні) і 2 (у вихідного отвору)

[math]\frac{{V_{}2}^{2}}{2}+\frac{patm}{\rho }+gz_{2}=\frac{p_{1}}{\rho }+gz_{1}[/math]

де ратм - атмосферний тиск у вихідного отвору. Звідси легко отримати формулу для швидкості закінчення V2. В окремому випадку ратм = р1 отримуємо так звану формулу Торічеллі для витікання рідини з широкого посудини з вузьким вихідним отвором.

[math]V_{2}=\sqrt{2gh}[/math]

на ім'я італійського вченого Е. Торрічеллі (1608-1647). Тут h = (z1 - z2). Для ванни з висотою налитої води приблизно 0,5 м швидкість витікання V2 »3,1 м / сек.

Рівняння руху ідеальної рідини мають ще один інтеграл для нестаціонарних течій, який називається інтегралом Коші - Лагранжа. Він справедливий для течій, в яких відсутні вихори. Його часто, наприклад, використовують при розгляді хвильових рухів рідини чи газу.

Інтеграл Бернулі запропоновано Д.Бернуллі (D. Bernoulli, 1738)

Література

Милн-Томсон Л. М. «Теоретическая гидродинамика». пер. з англ., М., 1964.

Б. и. предложен Д. Бернулли (D. Bernoulli, 1738). Лит.:[1] Мил н-Томсон Л. М., Теоретическая гидродинамика, пер. с англ., М., 1964. Л. Н. Сретенский.