Теорема Жуковського
В основі аеродинаміки як науки закладена теорема Миколи Єгоровича Жуковського, видатного російського вченого, засновника аеродинаміки, яка була сформульована ще в 1904 році. Через рік, у листопаді 1905 року Жуковський виклав свою теорію створення підіймальної сили крила літаючого апарату на засіданні Математичного товариства.
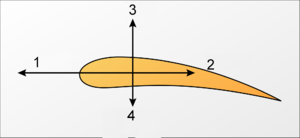
Теорема Жуковського, теорема про підіймальну силу, яка діє на тіло, що знаходиться в плоскопаралельному потоці рідини або газу. Згідно з цією теоремою, підіймальна сила, обумовлена пов'язаними з обтічним тілом вихорами (приєднаними вихорами), причиною виникнення яких є в'язкість рідини. Наявність цих вихорів приводить до обтікання крила потоком з відмінною від нуля циркуляцією швидкості.
[math]Y=\rho \upsilon \Gamma[/math]
Y - підіймальна сила; [math]\rho[/math] - густина; [math]\upsilon[/math] - швидкість руху незбуреного потоку; Г - циркуляція швидкості
[math]\Gamma = \int \upsilon dA[/math]
(dA — елемент контура)
Частина А, що трактує про рух стискуваної рідини (газу), називається газовою динамікою. Явище стисливості характеризують числом Маха [math]M= \upsilon /a[/math]
Якщо сталий плоскопаралельний потенційний потік нестискуваної рідини набігає на нескінченно довгий циліндр перпендикулярно його створюючим, то на ділянку циліндра, що має довжину уздовж створюючої, рівну одиниці, діє підіймальна сила Y, дорівнює добутку щільності (середовища на швидкість v потоку на нескінченності і на циркуляцію Г швидкості по будь-якому замкнутому контуру, що охоплює обтічний циліндр, тобто [math]Y=\rho \upsilon \Gamma[/math]. Напрям підіймальної сили виходить з напряму вектора швидкості на нескінченності його поворотe на прямий кут проти напряму циркуляції. Теорема Жуковського справедлива і при дозвуковому обтіканні профілю стискуваною рідиною (газом). Для звукової і надзвукових швидкостей обтікання ця теорема в загальному вигляді не може бути доведена.
Зміст
[сховати]Підіймальна сила
Підіймальна сила - складова повної сили тиску рідкого або газоподібного середовища на рухоме в ній тіло, направлена перпендикулярно до швидкості тіла (до швидкості центру тяжіння тіла, якщо воно рухається непоступально). Виникає унаслідок несиметрії обтікання тіла середовищем. Наприклад, при обтіканні крила літака частинки середовища, які оточують нижню поверхню, проходять за такий самий проміжок часу меншу відстань ніж частинки, оточуючі верхню, більш опуклу поверхню і, отже, мають меншу швидкість. Але, згідно рівняння Бернулі там, де швидкість частинок менша, тиск середовища більший і навпаки. В результаті тиск середовища на нижню поверхню крила буде більший, ніж на верхню, що і призводить до появи піднімальної сили.
Несиметричне обтікання крила можна представити як результат накладення на симетричну течію циркуляційного потоку навколо контуру крила, направленого на більш опуклу частину поверхні у бік течії, що призводить до збільшення швидкості, а на менш опуклою — проти течії, що приводить до її зменшення. Тоді піднімальна сила Y залежатиме від величини циркуляції швидкості [math]\Gamma[/math] і, згідно теоремі Жуковського, для ділянки крила довжиною L, обтічного плоскопаралельним потоком ідеальної нестискуваної рідини, [math]Y=ru\Gamma l[/math], де r — щільність середовища, u — швидкість набігаючого потоку.
Оскільки [math]\Gamma[/math] має розмірність [math]\left [ u\times I \right ][/math], то піднімальну силу можна виразити рівністю [math]Y=\frac{c_{B}rSu^{2}}{2}[/math] зазвичай вживаним, в аеродинаміці де S— величина характерної для тіла площі (наприклад, площа крила), [math]c_{b}[/math] — безрозмірний коефіцієнт піднімальної сили залежний від форми тіла, його орієнтації в середовищі і чисел Рейнольдса [math]Re[/math] і Маху [math]M[/math]. Значення [math]c_{B}[/math] в визначають теоретичним розрахунком або експериментально. Так, згідно теорії Жуковського, для крила в плоскопаралельному потоці [math]Вставте сюди формулу[/math], де [math]a[/math] — кут атаки (кут між напрямом швидкості набігаючого потоку і хордою крила), a [math]a_{0}[/math] — нульовий кут піднімальної сили, m — коефіцієнт, залежний лише від форми профілю крила, наприклад, для тонкої зігнутої пластини [math]m=p[/math] . В разі кінцевого розмаху / крила коефіцієнт [math]m=\frac{p}{(1-\frac{2}{I})}[/math], де [math]I=\frac{I^{2}}{S}[/math] — подовження крила.
В реальній рідині в результаті впливу в'язкості величина [math]m[/math] менш теоретична, причому ця різниця зростає у міру збільшення відносної товщини профілю; значення кута [math]a_{0}[/math] також менш теоретичного. Крім того, із збільшенням кута [math]a[/math] залежність [math]c_{B}[/math] в від [math]a[/math], перестає бути лінійною і величина [math]dc_{B}/d_{a}[/math] монотонно убуває, стаючи рівною нулю при куті атаки [math]a[/math]кр , якому відповідає максимальна величина коефіцієнта піднімальної сили. — [math]c_{y; max}[/math]. Подальше збільшення [math]a[/math] веде до падіння [math]c_{B}[/math] унаслідок відриву пограничного шару від верхньої поверхні крила. Величина [math]c_{y; max}[/math] має істотне значення, отже, чим вона більша, тим менша швидкість зльоту і посадки літака.
При надзвукових швидкостях характер обтікання істотно змінюється. Так, при обтіканні плоскої пластини на передній кромці верхньої поверхні утворюються хвилі розрідження, а на нижній — ударна хвиля. В результаті тиск [math]p_{H}[/math] на нижній поверхні пластини стає більшим, ніж на верхній ( [math]p_{B}[/math] ) ; виникає сумарна сила, нормальна до поверхні пластини складова якої, перпендикулярна до швидкості набігаючого потоку, і є піднімальною силою.
Доведення Теореми Жуковського
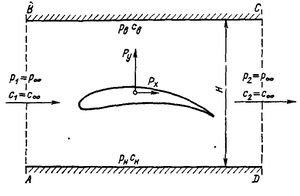
Для доведення теореми скористаємося схемою, що на малюнку. Тут профіль крила розташовується в плоскому потоці між двома нескінченно довгими непроникними плоскими поверхнями, орієнтованими по потоці і віддаленими один від одного на відстань [math]H \to \propto[/math]. Зв'яжемо систему координат з профілем і направимо вісь [math]x[/math] вздовж потоку. Далі проведемо перед профілем і за ним два контрольних перетини АВ і CD на такій відстані від профілю, щоб збурення, що вносяться профілем в цих перетинах, були нескінченно малими і, отже, всі швидкості і параметри потоку були однаковими.
До маси рідини, обмеженою контрольними поверхнями, застосуємо теорему зміни кількості руху, вважаючи, що розглянутий профіль обтікаєтся безвідривно.
Проектуючи рівняння кількості руху на вісь [math]x[/math], отримуємо
[math]\int_{H} \left ( p_{1}-p_{2} \right )dy-P_{x}-\int_{H}p_{1}c_{1}\left ( c_{1}-c_{2} \right )dy=0[/math]
Оскільки згідно з прийнятим розташуванням перерізів АВ і CD [math]c_{1}=c_{2}=c_{\propto }[/math], і [math]p_{1}=p_{2}=p_{\propto }[/math] то [math]P_{\propto }=0[/math] . Цей результат узагальнює парадокс Ейлера-Даламбера на тіла довільної форми, які обтікає ідеальна рідина без відриву потоку. Вертикальну складову сили впливу потоку на профіль (підіймальну силу) [math]P_{y}[/math] знайдемо, складаючи рівняння кількості руху в проекції на вісь [math]y[/math]:
[math]-P_{y}+\int_{-\propto }^{+\propto }\left ( p_{H}-p_{B} \right )dx=0[/math]
Звідси
[math]P_{y}=\int_{-\propto }^{+\propto }\left ( p_{H}-p_{B} \right )dx[/math]; (1)
Якщо розмір H між поверхнями AD і ВС достатньо великий, то швидкості уздовж цих поверхонь будуть відрізнятися від швидкості потоку, що набігає на малі величини [math]{c}'_{H}[/math] і [math]{c}'_{B}[/math]. Тоді дійсні швидкості [math]{c}_{H}[/math] і [math]{c}_{B}[/math] можна представити у вигляді суми постійної складової [math]{c}_{\propto }[/math], і малих величин [math]{c}'_{H}[/math] і [math]{c}'_{B}[/math], квадратами яких можна знехтувати:
[math]\left.\begin{matrix} c_{H}={c}_{\propto }+{c}'_{H}; \\ c_{B}={c}_{\propto }+{c}'_{B}. \end{matrix}\right\}[/math] (2)
Використовуючи це подання швидкостей і рівняння Бернуллі для стискуваної рідини, знайдемо тиск у довільній точці збуреного потоку біля контрольної поверхні
[math]\frac{p}{\rho }=\frac{p_{\propto }}{\rho _{\propto }}+\frac{k-1}{2k}\left ( c_{\propto }^{2}-c^{2}\right )=\frac{p_{\propto }}{\rho _{\propto }}+\frac{k-1}{2k}\left ( c_{\propto }^{2}-c_{\propto }^{2}+2c_{\propto }{c}'-{c}'^{2}\right )\approx \frac{p_{\propto }}{\rho _{\propto }}-\frac{k-1}{k}c_{\propto }{c}'[/math]
Так як з урахуванням рівняння ізотропи [math]\rho =\rho _{\propto }\left ( \frac{p}{p_{\propto}}\right )^{\frac{1}{k}}[/math], a [math]\frac{kp_{\propto }}{\rho _{\propto }}=a_{\propto }^{2}[/math], то після нескладних перетворень знаходимо
[math]p/p_{\propto }=\left [ 1-(k-1)M_{\propto }^{2}\frac{{c}'}{c_{\propto }} \right ]^{\frac{k}{k-1}}[/math]
Розкладаючи вираз у квадратних дужках в ряд і обмежуючись двома членами розкладання, отримуємо
[math]\frac{p}{p_{\propto }}=1-kM_{\propto }^{2}\frac{{c}'}{c_{\propto }}=1-\frac{kc_{\propto }{c}'}{a_{\propto }^{2}}=1-\frac{c_{\propto }{c}'}{p_{\propto }}p_{\propto }[/math]
або
[math]p=p_{\propto }-\rho _{\propto }c_{\propto }{c}'[/math]; (3)
Рівняння (3) називають лінеаризованим рівнянням Бернуллі. Запишемо (3) для верхньої і нижньої контрольних поверхонь:
[math]\left.\begin{matrix} p_{B}=p_{\propto }-\rho _{\propto }c_{\propto }{c}'_{B}; \\ p_{H}=p_{\propto }-\rho _{\propto }c_{\propto }{c}'_{H}. \end{matrix}\right\}[/math] (4)
Підстановка залежностей (4) у рівняння (1) дає
[math]P_{y}=\rho _{\propto }c_{\propto }\int_{-\propto }^{+\propto }\left ( {c}'_{B}-{c}'_{H} \right )dx[/math]
Покажемо, що значення інтеграла в цьому рівнянні можна виразити через циркуляцію швидкості по замкнутому контуру ADCBA (див. малюнок). В дійсності
[math]\Gamma _{ADCBA}=\Gamma _{AD}+\Gamma _{DC}+\Gamma _{CB}+\Gamma _{BA}[/math]
Так як
[math]\Gamma_{AD}=+\int_{-\propto }^{+\propto }\left ( c_{\propto }+ {c}_{H}' \right )dx[/math]; [math]\Gamma_{CB}=-\int_{-\propto }^{+\propto }\left ( c_{\propto }+ {c}_{B}' \right )dx[/math]; [math]\Gamma _{BA}=-\Gamma _{DC}[/math],
то
[math]\Gamma _{ADCBA}=-\int_{-\propto }^{+\propto }\left ( {c}'_{B}-{c}'_{H} \right )dx[/math].
отже,
[math]P_{y}=\rho _{\propto }c_{\propto }\Gamma[/math]; (5)
що виражає наступну фундаментальну теорему гідрогазодинаміки:
при обтіканні тіла плоскопаралельним безмежним потоком ідеальної стисливої рідини на тіло одиничного розмаху діє сила, що дорівнює добутку щільності і швидкості потоку, який набігає на циркуляцію швидкості навколо обтічного тіла. Якщо вектор швидкості [math]c_{\propto }[/math], повернути на 90 ° у бік, протилежний напрямку циркуляції, то він вкаже напрямок дії підіймальної сили.
Знак мінус у формулі (5) відповідає прийнятому правилу знака для циркуляції [math]\Gamma[/math] і швидкості [math]c_{\propto }[/math]. Якщо, наприклад, швидкість спрямована в позитивну сторону осі [math]x[/math], а циркуляція спрямована за годинниковою стрілкою [math]\left (\Gamma \lt 1 \right )[/math], то підйомна сила позитивна.
Використання Теореми
Теорема Жуковського лягла в основу сучасної теорії крила і гребного гвинта. З її допомогою можуть бути обчислені підйомна сила крила кінцевого розмаху, тяга гребного гвинта, сила тиску на лопатку турбіни і компресора та ін.
Вона придатна для будь якого контуру, який обтікає плоско паралельний потік ідеальної рідини, але якщо пластина дуже тонка то обтікання передньої кромки є відривним, у цьому випадку Теорема Жуковського не застосовується.
Теорема Жуковського про підіймальну силу справедлива і для надзвукового обтікання пластини ідеальним газом, яке є циркуляційним і підіймальна сила відмінна від нуля.
Джерела і посилання
1. Гидрогазодинимика (для студентов вузов) - М. Е. Дейч; А. Е. Зарянкин/ Москва «Энергоатомиздат» , 1984, - 384с.
2. Прикладная гидрогазодинамика: Учебник для авиационных вузов. - Сергель О.С. / Москва «Машиностроение», 1981. – 374с.