Метод ковзного середнього
| {{{img}}} | ||
| Імя | Тарас | |
| Прізвище | Куриляк | |
| По-батькові | Тарасович | |
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | № ПК 08-108 | |
Ковзне середнє (англ. Moving Average - MA) – інструмент згладжування часових рядів, застосовуваний головним чином для відображення змін біржових котирувань акцій, цін на сировину і так далі. MA – один з найстаріших і найбільш поширених інструментів технічного аналізу. MA показує середнє значення ціни за певний період часу.
Зміст
Види ковзних середніх
Існує декілька видів ковзних середніх:
- просте ковзне середнє (SMA);
- експоненційне ковзне середнє (EMA);
- зважене ковзне середнє (WMA);
- трикутне ковзне середнє (TMA);
- адаптивне ковзне середнє (AMA);
- синус-зважене ковзне середнє (SWMA);
- ковзне середнє кінцевої точки (EPMA);
- та інші, менш поширені.
з яких найбільш поширеними є перші три.
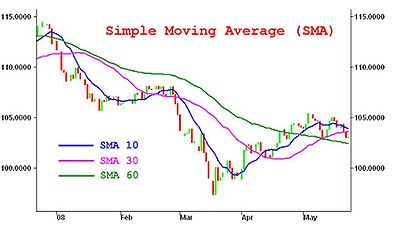
Просте ковзне середнє
Просте ковзне середнє (англ. Simple Moving Average – SMA) – є одними з найбільш простих і популярних індикаторів в технічному аналізі. SMA є звичайним середнім арифметичним від цін за певний період. SMA відноситься до класу індикаторів, які слідують за трендом, воно допомагає визначити початок нової тенденції і її завершення, за його кутом нахилу можна визначити силу (швидкість руху), воно ж в якості основи (або згладжуючого фактора) застосовується у великій кількості інших технічних індикаторів. Іноді ковзне середнє називають лінією тренда.
Формула простого ковзного середнього:
- [math]SMA = \frac{\sum_{i=1}^{n}P_i}{n}[/math]
де [math]P_i[/math] – ціни на ринку;
- n – основний параметр – довжина згладжування або період SMA (кількість цін що входять у розрахунок ковзного). Іноді цей параметр називають порядком змінного середнього.
Просте ковзне середнє є звичайним середнім арифметичним від цін за певний період. SMA являє собою якийсь показник ціни рівноваги за певний період, чим коротше SMA, тим за менший період береться рівновага. Усереднюючи ціни, воно завжди слідує за головною тенденцією ринку, фільтруючи дрібні коливання. Чим менший параметр SMA (коротке ковзне середнє), тим швидше воно визначає нову тенденцію, але й одночасно робить більше помилкових коливань, і навпаки чим більший параметр (довге ковзне середнє), тим повільніше визначається новий тренд, але надходить менше помилкових коливань.
Недоліки методу ковзного середнього
При використанні методу SMA для торгівлі по тренду запізнювання на вході і на виході з тренда як правило дуже значне, тому в більшості випадків втрачається велика частина трендового руху.
Один з найбільш серйозних недоліків методу SMA, полягає в тому що воно надає однакові ваги як новими цінами, так і більш старими, хоча логічніше було б припустити, що нові ціни важливіші, тому що відображають більш близьку ринкову ситуацію до поточного моменту.
Зважене ковзне середнє
Зважене ковзне середнє (англ. Weighted Moving Average – WMA). Одним з недоліків SMA є присвоєння при його розрахунку всім цінам однакових ваг при усередненні незалежно від того, ближче чи далі вони від поточного моменту. Цей недолік усунуто у зваженому ковзному середньому. WMA, таким чином, є звичайною модифікацією SMA з вагами підібраними так, що останні ціни мають більшу вагу.
Зважене ковзне середнє визначається за формулою:
- [math]WMA = \frac{\sum_{i=1}^{n}P_i*W_i}{\sum_{i=1}^{n}W_i}[/math]
де [math]P_i[/math] – значення ціни i-періодів тому, (i сьогодні = 1);
- [math]W_i[/math] – значення ваг для ціни i-періодів тому.
Зважене ковзне середнє являє собою арифметичне зважене коливань цін за певний період. В якості аналітичного інструменту воно знімає частину недоліків звичайного ковзного, але не усуває їх повністю.
Експоненційне ковзне середнє
Експоненційне ковзне середнє (англ. Exponential Moving Average – EMA) зменшує помилку, надаючи більшу вагу останнім цінами у порівнянні з більш далекими цінами. Цей метод дозволяє більш швидко реагувати на поточні зміни ціни в порівнянні з SMA. Вага, що надається останній ціні, залежить від періоду ковзної середньої. Чим коротший період EMA, тим більша вага надаватиметься останньою ціною.
Експоненційне ковзне середнє може бути визначене двома шляхами – як відсоткове ковзне середнє або як періодичне ковзне середнє. Відповідно в відсотковому ковзному, єдиним параметром є вага (відсоток), а в періодній – період КС.
Основна формула виглядає наступним чином:
- [math]EMA = \frac{EMA_{i-1}*(n-1)+2*P_i}{n+1}[/math]
де EMA – експонентна ковзна середня;
- [math]P_i[/math] – значення ціни в i-му періоді;
- n – період розрахунку;
- [math]EMA_{i-1}[/math] – значення ЕМА попереднього періоду.
Необхідно зазначити, що теоретично в розрахунку цієї ковзної використовуються всі ціни, за весь період її побудови і, незважаючи на те, що вплив старих цін зникає з часом, він не зникає до кінця. Ефект старих цін зникає швидше для більш коротких EMA, в порівнянні з більш довгими. На реальному графіку різниця між SMA і EMA не дуже велика, хоча і є присутня. Вважається, що експоненційне ковзне все ж краще відображає ринкові ціни при інших рівних умовах, оскільки вплив кожної попередньї ціни убуває експоненційно з його віддаленістю від поточної ціни.
Перелік літературних джерел
- Виды средних скользящих (SMA, EMA, WMA)
- Скользящие средние
- Скользящие средние значения
- Скользящие средние. Типы СС
- Побудова середніх ковзних
- Технические индикаторы II: Скользящие средние
- Технический анализ Forex (Форекс)

- Студент: Користувач:Куриляк Тарас Тарасович
- Виступ відбувся: 23 грудня 2010
- Тема: Метод ковзного середнього