Метод випадкового пошуку і сканування
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
| Цю статтю потрібно відредагувати. Щоб вона відповідала ВИМОГАМ. |
| {{{img}}} | ||
| Імя | Тарас | |
| Прізвище | Івасюк | |
| По-батькові | Анатолійович | |
| Факультет | ФІС | |
| Група | СН-51 | |
| Залікова книжка | СН-10-055 | |
Зміст
Метод випадкового пошуку і сканування
Якщо відомо, що функція відклику має не один, а кілька максимумів (мінімумів), то для відшукування найекстремальнішого з них, тобто справжнього оптимуму функції, застосовують один з двох методів деякою мірою протилежних один одному.
Перший метод
Перший метод (група методів) — це метод випадкового пошуку. Як свідчить назва, в них заздалегідь не задається програма пошуку оптимуму. Розглянемо детальніше один з найхарактерніших методів цієї групи — метод випадкових напрямів. Його особливістю є випадковий вибір напряму подальшого руху в кожній новій точці, досягнутій після k кроків. Припустимо, що точка, в яку ми прийшли через k кроків, займає у факторному просторі положення [math]\vec{(x_k)}[/math] (рис.1).
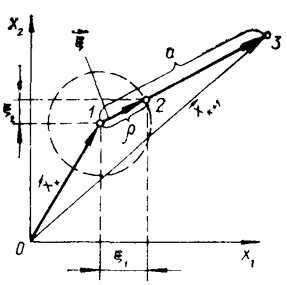
З цієї точки у випадковому напрямі вектора [math]\vec z[/math] виконується пробний крок фіксованої довжини. Геометричне місце точок рівноможливих координат пробного експерименту кінців випадкового вектора z зображено у вигляді кола кожна точка якого може бути задана у випадку двох координат парою випадкових чисел [math]z_1[/math] і [math]z_2[/math]- Умова сталої довжини пробного кроку:
забезпечується тим, що вказані випадкові числа [math]z_1[/math] і [math]z_2[/math] зв'язуються співвідношенням:
Координата пробного кроку [math]\vec{x_k}+\vec z[/math] дає можливість вимірювати значення функції відклику [math]y(\vec{x_k}+\vec z)[/math]. Утворене значення порівнюється з відкликом у раніше досягнутій точці з координатою [math]\vec(x_k)[/math], після чого виконується (k+1)- й робочий крок у напрямі вектора [math]\vec z[/math] в бік збільшення значення y. Звичайно довжина робочого кроку a перевищує величину пробного, тобто а > р. Для практичного застосування методу випадкового пощуку використовують такий алгоритм:
1) визначають початкову точку [math]\vec(x_1)[/math] у факторному просторі змінних [math]{x_n};[/math]
2) задають довжини пробного і робочого кроків, відповідно р і а;
3) обчислюють координати [math]z_1, z_2, z_3, ..., z_n[/math] вектора [math]\vec z,[/math] що визначає напрям руху з початкової точки.
Вектор [math]\vec z[/math] рівномірно розподілено на n-вимірній сфері. Для n=2 може бути запропоновано спрощену процедуру формування вектора [math]\vec z[/math]. З таблиці випадкових чисел вибирають рівномірно розподілене на відрізку [0, +p] випадкове число [math]z_1[/math], яке беруть за один з компонентів вектора [math]\vec z[/math].
Другий компонент обчислюють за формулою
Знаки [math]z_1[/math] і [math]z_2[/math] визначають залежно від парності або непарності відповідно попереднього [math]z_1[/math] і наступного за ним випадкового числа. Так, якщо число, яке стоїть перед [math]z_1[/math] — парне, то для [math]z_1[/math] беруть знак (+); аналогічно — для [math]z_2[/math].
Слід зазначити, що описаний спосіб формування вектора [math]\vec z[/math] не забезпечує строго рівномірного розподілу його по колу радіуса р, проте для багатьох практичних задач таке набли¬ження є достатнім;
4) виконують два пробних експерименти в точках [math]\vec x[/math] і [math]\vec x + \vec z[/math]. На рис.1 зображені точки мають номери відповідно 1 і 2.
Внаслідок порівняння відповідних значень відкликів [math]y(\vec x +\vec z)[/math] і [math]y(\vec x)[/math] формується
5) здійснюють робочий крок (довжиною а) у напрямі зростання рівня виходу, тобто в точку 3
6) у точці 3 процедура повністю повторюється, очевидно, для (k + 1)-ї точки матимемо
7) якщо після k-го кроку пробного експерименту виявиться
то питання про те, в який бік за напрямом вектора z здійснити робочий крок, вирішується випадковим чином (наприклад, підкиданням монети);
8) критерієм виходу в область екстремуму цільової функції є зростання числа невдалих кроків, тобто багаторазове повторення ситуації
Рекомендована кількість невдалих спроб, звичайно, становить 20—ЗО.
Другий метод
Це метод повного перебору або сканування. Він полягає у послідовному перегляді значень параметра оптимізації по всій поверхні функції відклику та знаходженні серед точок цієї поверхні такої, в якій параметр оптимізації має оптимальне значення. Точність методу визначається тим, наскільки щільно розташовуються вибрані точки в припустимій області зміни змінних, тобто кроком квадратної (кубічної, гіперкубічної) решітки, у вузлах якої ставляться досліди. Перевагою методу сканування є те, що при досить щільному розміщенні точок гарантується відшукання глобального оптимуму, оскільки аналізується вся область зміни незалежних змінних, а також незалежність пошуку від вигляду оптимізованої функції. Загальний недолік майже всіх градієнтних методів полягає в тому, що вони застряють в найближчому локальному оптимумі, в область тяжіння якого попадає обрана початкова точка руху. На відміну від цих методів, метод сканування ніяк не пов'язаний з наявністю локальних оптимумів цільової функції. Тому іноді його можна використати для попереднього грубого встановлення меж областей тяжіння локальних оптимумів, після чого можуть вживатися градієнтні методи. До недоліків методу належить необхідність обчислення значень функції відклику для великої кількості точок. Найпростіший алгоритм пошуку методом сканування, який іноді називають пошуком по сітці змінних, полягає в тому, що при заданому значенні однієї змінної [math]x_i[/math], для ряду значень іншої змінної [math]x_j[/math], віддалених одна від одної на величину кроку [math]\triangle x[/math], визначаються значення параметра опти мізацІЇ. При довільній кількості незалежних змінних крок по кожній наступній змінній провадиться після того, коли повністю завершено цикл рухів за попередньою змінною. Існує кілька модифікацій методу сканування, вживаних, в основному, для скорочення обсягу обчислень. Одна з них це алгоритм зі змінним кроком сканування. Спочатку величина кроку вибирається досить великою і виконується грубий пошук. Після того, як область глобального оптимуму визначено, здійснюється пошук з меншим кроком у межах вказаної області. Розвиток обчислювальної техніки приводить до того, що метод повного перебору найчастіше використовується при оптимізації сільськогосподарських та технологічних процесів у чистому вигляді або в поєднанні з імітаційними (математичними) експериментами.
Список використаних джерел
1. Математичне планування експериментів в АПК / В. О. Аністратенко, В. Г. Федоров.-К.:Вища школа,1993.-374с.