Метод випадкового балансу
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
| Цю статтю потрібно відредагувати. Щоб вона відповідала ВИМОГАМ. |
| {{{img}}} | ||
| Імя | Тарас | |
| Прізвище | Івасюк | |
| По-батькові | Анатолійович | |
| Факультет | ФІС | |
| Група | СН-51 | |
| Залікова книжка | СН-10-055 | |
Зміст
Вступ
Цей метод є одним із способів відсіювання факторів при підготовці активного експерименту. У випадку, коли відомо усі сукупності досліджуваних змінних і тільки деякі з них є дійсно істотними, а решта можуть бути віднесені до шумового поля, бажано провести кілька експериментів за методом випадкового балансу, при цьому виділяються лише ті фактори, які значно впливають на вихідну величину або, як ще часто її називають, цільову функцію.
Ідея методу
Основна ідея методу полягає в тому, що замість дробових реплік, якими є систематичні вибірки з ПФЕ, пропонується брати випадкові вибірки. При цьому спільні оцінки беруть змішаними. Планування відсіювальних експериментів робиться так, що число дослідів N пов'язане з числом n досліджуваних ефектів, до яких належать самі фактори та їх парні взаємодії, такою нерівністю:
Формально ця нерівність означає, що число ступенів вільності f стає від'ємною величиною. При f<0 не можна дати кількісної оцінки всім коефіцієнтам регресії. Проте цього і не вимагається при проведенні відсіювальних ек¬спериментів. На першому етапі достатньо провести попереднє розщеплення математичної моделі, зарахувавши більшу частину ефектів до шумового поля. Тоді решту ефектів можна буде оцінити кількісно. При цьому оцінка решти коефіцієнтів регресії провадитиметься з тим меншою похибкою, чим меншою буде дисперсія шумового поля.
Чутливість методу
Існує поняття чутливість методу, яке характеризує здатність виділяти коефіцієнти регресії, що значно відрізняються від нуля, тобто відхиляти нуль-гіпотезу [math]b_i=0[/math]. З точки зору чутливості метод випадкового балансу набагато гірший, ніж повний або дробовий факторні експерименти, проте він має велику роздільну здатність і в сприятливих умовах дає змогу виділяти роздільно домінуючі ефекти серед великої кількості ефектів, взятих для розгляду.
Основні етапи методу випадкового балансу
Побудова матриці планування для проведення відсіювальних експериментів здійснюється так. Усі лінійні ефекти розбиваються на групи. Це іноді пов'язують з фізикою процесу, а іноді проводять формально. При цьому число факторів у групі не повинно перевищувати п'яти-шести. Потім для кожної групи будують матрицю планування, проводячи ДФЕ або ПФЕ. Краще компонувати групу з двох — чотирьох елементів, вибираючи для групи відповідний ПФЕ, оскільки при цьому перебираються всі можливі комбінації рівнів у групі. План проведення експерименту методом випадкового балансу утворюється випадковим змішуванням рядків відповідних групових планів.
Наступним етапом методу випадкового балансу є послідовне виділення істотних параметрів. Виділення значущих ефектів та розташування їх за рангом впливу (ранжирування) здійснюється з використанням здобутих внесків за допомогою такої процедури. Послідовно виключають вплив найбільш істотних параметрів, ніби стабілізуючи їх на одному рівні.
Розглянемо поняття видільної точки, розглянемо діаграму розсіювання для деяких факторів [math]{}^-\!x_1^+[/math] і [math]{}^-\!x_2^+[/math]
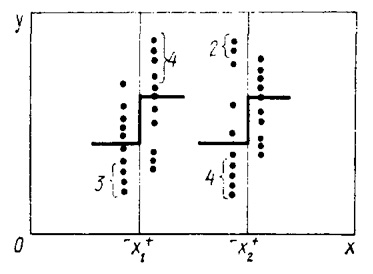
На рівні [math]x_1^+[/math] є чотири точки, для яких значення виходу більше, ніж найбільше значення виходу на рівні [math]x_1^-[/math]. Аналогічно на рівні [math]x_1^-[/math] є три точки, для яких вихід менший, ніж найнижчий вихід на рівні [math]x_1^+[/math]. Сумарна кількість видільних точок для фактора [math]x_1[/math] становить 4 + 3 = 7. Для фактора [math]x_2[/math] є лише шість видільних точок. Фактор [math]x_1[/math] вважається істотнішим. Процес виділення істотних параметрів припиняється, коли на черговій діаграмі розсіювання всі внески беруть приблизно одного порядку і незначними за величиною. Решта ефектів належить до шумового поля. Для виділення факторів іноді дістають грубу оцінку коефіціентів при лінійних ефектах і парних взаємодіях. Відповідні коефіцієнти визначають за формулами:
Вільний член рівняння визначають відношенням:
Хоча без паралельних дослідів не можна перевірити значущість утворених коефіцієнтів, вони можуть бути корисними у попередніх розрахунках за ПФЕ і ДФЕ.
Описаний вище порядок ранжирування факторів за мегодом випадкових балансів є досить трудомісткою процедурою, особливо при великому числі факторів.
Ефективність викладеного методу може бути підвищеною, якщо на кожному етапі дослідження виділяти не окремий внесок [math]B_x_i[/math] або [math]B_x_i_x_j[/math], а групу факторів з найвищими внесками, які мають однаковий порядок.
У кожній клітинці записують відповідну кількість [math]N_j[/math] (j=1,2,...) значень вихідного параметру [math]y_j_k[/math] і знаходять середнє для кожної клітини:
Після коректування та побудови нової діаграми розсіювання, виділяжться нова група і т. д.
Список використаних джерел
1. Математичне планування експериментів в АПК / В. О. Аністратенко, В. Г. Федоров.-К.:Вища школа,1993.-374с.