Методи прогнозування
| Цю статтю потрібно відредагувати. Щоб вона відповідала ВИМОГАМ. |
| {{{img}}} | ||
| Імя | Євген | |
| Прізвище | Олійник | |
| По-батькові | ||
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | ||
http://elartu.tstu.edu.ua/handle/123456789/411 Презентація доповіді (університетський репозиторій).
Зміст
Методи прогнозування
До недавнього часу (середини 80-х років минулого століття) існувало декілька загальновизнаних методів прогнозування тимчасових рядів:
• Економетричні
• Регресійні
• Методи Бокса-дженкінса (ARIMA, ARMA)
Проте, починаючи з кінця 80-х років, в науковій літературі були опубліковані ряд статей з нейромережевої тематики, в яких був приведений ефективний алгоритм навчання нейронних мереж і доведена можливість їх використання для найширшого кола завдань.
Ці статті відродили інтерес до нейромереж в науковому співтоваристві і останні дуже скоро почали широко використовуватися при дослідженнях в самих різних областях науки від експериментальної фізики і хімії до економіки.
Методи прогнозування, засновані на згладжуванні, експоненційному згладжуванні і ковзному середньому
"Наївні" моделі прогнозування
При створенні "наївних" моделей передбачається, що деякий основний період прогнозованого тимчасового ряду краще всього описує майбутнє цього прогнозованого ряду, тому в цих моделях прогноз, як правило, є дуже простою функцією від значень прогнозованої змінної в недалекому минулому.
Найпростішою моделлю є
що відповідає припущенню, що "завтра буде як сьогодні"[4].
Поза всяким сумнівом, від такої примітивної моделі не варто чекати великої точності. Вона не тільки не враховує механізми, що визначають прогнозовані дані (цей серйозний недолік взагалі притаменний багатьом статистичним методам прогнозування), але і не захищена від випадкових коливань, вона не враховує сезонні коливання і тенденції. Втім, можна будувати "наївні" моделі дещо по-іншому
[math]\begin{align} & Y_{t+1}=Y_{t}+\left[ Y_{t}-Y_{t-1} \right], \\ & Y_{t+1}=Y_{t}\cdot \left[ Y_{t}/Y_{t-1} \right], \\ \end{align}[/math]
такими способами ми намагаємося пристосувати модель до можливих тенденцій
[math]Y_{t+1}=Y_{t-S}[/math]
це спроба врахувати сезонні коливання.
Середні і ковзаючі середні
Найпростішою моделлю, заснованою на простому усереднюванні [4] є
[math]Y_{t+1}=\frac{1}{t}\left[ Y_{t}+Y_{t-1}+...+Y_{1} \right][/math]
і у відмінності від найпростішої "наївної" моделі, якій відповідав принцип "завтра буде як сьогодні", цій моделі відповідає принцип "завтра буде як було в середньому за останній час". Така модель, звичайно стійкіша до коливань, оскільки в ній згладжуються випадкові викиди щодо середнього. Не дивлячись на це, цей метод ідеологічно настільки ж примітивний як і "наївні" моделі і йому властиві майже ті ж самі недоліки.
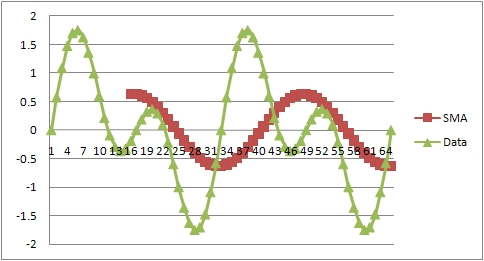
У приведеній вище формулі передбачалося, що ряд усереднюється по достатньо тривалому інтервалу часу. Проте як правило, значення тимчасового ряду з недалекого минулого краще описують прогноз, ніж усі попередні значення цього ж ряду. Тоді можна використовувати для прогнозування ковзне середнє
[math]Y_{t+1}=\frac{1}{T+1}\left[ Y_{t}+Y_{t-1}+...+Y_{t-T} \right][/math]
Сенс його полягає в тому, що модель бачить тільки найближче минуле (на T відліків за часом в глибину) і грунтуючись тільки на цих даних будує прогноз.
При прогнозуванні досить часто використовується метод експоненціальних середніх, який постійно адаптується до даних за рахунок нових значень. Формула, що описує цю модель записується як
де [math]Y_{t+1}[/math] – прогноз на наступний період часу
[math]Y_{t}[/math] – реальне значення у момент часу t
[math]\hat{Y}[/math] – минулий прогноз на момент часу t
а – постійна згладжування (0<=a<=1)
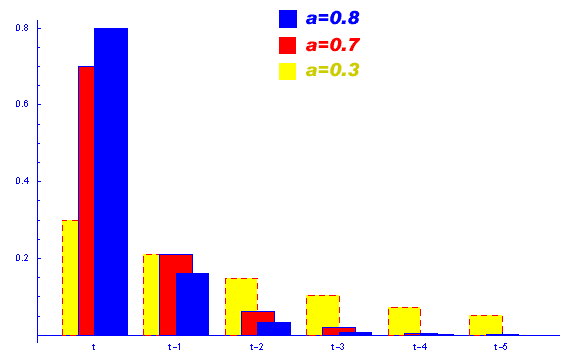
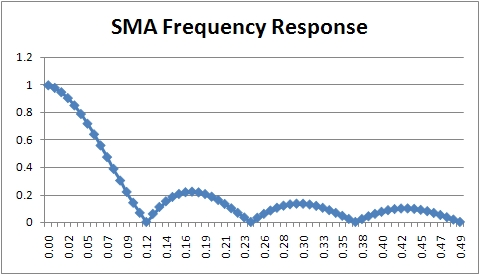
У цьому методі є внутрішній параметр а, який визначає залежність прогнозу від усіх розглянутих даних, причому вплив даних на прогноз експоненціально зменшується із "віком" даних. Залежність впливу даних на прогноз при різних коефіцієнтах а приведена на графіці.
Видно, що при a→1, експоненціальна модель прагне до найпростішої "наївної" моделі. При a→0, прогнозована величина стає рівною попередньому прогнозу.
Якщо проводиться прогнозування з використанням моделі експоненціального згладжування, зазвичай на деякому тестовому наборі будуються прогнози при a=[0.01, 0.02 ..., 0.98, 0.99] і відстежується, при якому а точність прогнозування вища. Це значення а потім використовується при прогнозуванні надалі.
Хоча описані вище моделі ("наївні" алгоритми, методи, засновані на середніх, ковзних середніх і експоненціальному згладжуванні) використовуються при бізнес-прогнозуванні в не дуже складних ситуаціях, наприклад, при прогнозуванні продажу на спокійних і сталих західних ринках, не рекомендовано використовувати ці методи в завданнях прогнозування з причини явної примітивності і неадекватності моделей.
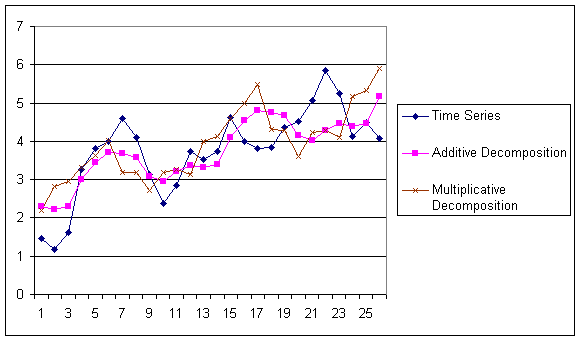
Разом з цим хотілося б відзначити, що описані алгоритми цілком успішно можна використовувати як супутні і допоміжні для передобробки даних в завданнях прогнозування. Наприклад, для прогнозування продажу в більшості випадків необхідно проводити декомпозицію тимчасових рядів (тобто виділяти окремо тенденційну, сезонну і нерегулярну складові). Одним з методів виділення тенденційних складових є використання експоненціального згладжування.
Методи Хольта і Брауна
В середині минулого століття Хольт запропонував вдосконалений метод експоненціального згладжування, згодом названий його ім'ям. У запропонованому алгоритмі значення рівня і тенденції згладжуються за допомогою експоненціального згладжування. Причому параметри згладжування у них різні.
[math]\left\{ \begin{matrix}
\Omega _{t}=\alpha Y_{t}+\left( 1-\alpha \right)\left( \Omega _{t-1}-T_{t-1} \right), \\
T_{t}=\beta \left( \Omega _{t}-\Omega _{t-1} \right)+\left( 1-\beta \right)T_{t-1}, \\
\hat{Y}_{t+p}=\Omega _{t}+pT_{t} \\
\end{matrix} \right.[/math]
Тут перше рівняння описує згладжений ряд загального рівня.
Друге рівняння служить для оцінки тенденції.
Третє рівняння визначає прогноз на p відліків за часом вперед.
Постійні згладжування в методі Хольта ідеологічно грають ту ж роль, що і постійна в простому експоненціальному згладжуванні. Підбираються вони, наприклад, шляхом перебору по цих параметрах з якимсь кроком. Можна використовувати і менш складні в сенсі кількості обчислень алгоритми. Головне, що завжди можна підібрати таку пару параметрів, яка дає велику точність моделі на тестовому наборі і потім використовувати цю пару параметрів при реальному прогнозуванні.
Окремим випадком методу Хольта є метод Брауна, коли [math]\alpha =\beta[/math] .
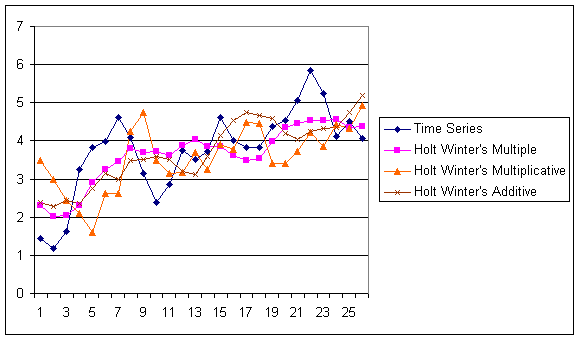
Метод Вінтерса
Хоча описаний вище метод Хольта (метод двохпараметричного експоненціального згладжування) і не є зовсім простим (щодо "наївних" моделей і моделей, заснованих на усереднюванні), він не дозволяє враховувати сезонні коливання при прогнозуванні. Кажучи акуратніше, цей метод не може їх "бачити" в передісторії. Існує розширення методу Хольта до трьохпараметричного експоненціального згладжування. Цей алгоритм називається методом Вінтерса. При цьому робиться спроба врахувати сезонні складові даних. Система рівнянь, що описують метод Вінтерса виглядає таким чином:
[math]\left\{ \begin{matrix} \Omega _{t}=\alpha \frac{Y_{t}}{S_{t-s}}+\left( 1-\alpha \right)\left( \Omega _{t-1}-T_{t-1} \right), \\ T_{t}=\beta \left( \Omega _{t}-\Omega _{t-1} \right)+\left( 1-\beta \right)T_{t-1}, \\ S_{t}=\Upsilon \frac{Y_{t}}{\Omega _{t}}+\left( 1-\Upsilon \right)S_{t-s}, \\ \hat{Y}_{t+p}=\left( \Omega _{t}+pT_{t} \right)S_{t-s+p} \\ \end{matrix} \right.[/math]
Дріб в першому рівнянні служить для виключення сезонності з Y(t). Після виключення сезонності алгоритм працює з "чистими" даними, в яких немає сезонних коливань. З'являються вони вже в самому фінальному прогнозі, коли "чистий" прогноз, порахований майже по методу Хольта умножається на сезонний коефіцієнт.
Регресійні методи прогнозування
Разом з описаними вище методами, заснованими на експоненціальному згладжуванні, вже достатньо довгий час для прогнозування використовуються регресійні алгоритми. Коротко суть алгоритмів такого класу можна описати так. Існує прогнозована змінна Y (залежна змінна) і відібраний заздалегідь комплект змінних, від яких вона залежить, - X1, X2 ..., XN (незалежні змінні). Природа незалежних змінних може бути різною. Наприклад, якщо припустити, що Y - рівень попиту на деякий продукт в наступному місяці, то незалежними змінними можуть бути рівень попиту на цей же продукт в минулий і позаминулий місяці, витрати на рекламу, рівень платоспроможності населення, економічна обстановка, діяльність конкурентів і багато що інше. Головне - уміти формалізувати всі зовнішні чинники, від яких може залежати рівень попиту в числовій формі.
Модель множинної регресії в загальному випадку описується виразом
[math]Y=F\left( X_{1},\,X_{2},\,...,\,X_{N} \right)+\varepsilon[/math]
У простішому варіанті лінійної регресійної моделі залежність залежної змінної від незалежних має вигляд:
[math]Y=\beta _{0}+\beta _{1}X_{1}+\beta _{2}X_{2}+...+\beta _{N}X_{N}+\varepsilon[/math]
Тут [math]\beta _{1},\beta _{2},\,...,\,\beta _{N}-[/math] підбирані коефіцієнти регресії
[math]\varepsilon -[/math] компонента помилки. Передбачається, що всі помилки незалежні і нормально розподілені. Для побудови регресійних моделей необхідно мати базу даних спостережень приблизно такого вигляду:
| Змінні | |||||
|---|---|---|---|---|---|
Незалежні |
Залежна | ||||
| № | X1 | X2 | ... | XN | Y |
| 1 | x_11 | x_12 | ... | x_1N | Y_1 |
| 2 | x_21 | x_22 | ... | x_2N | Y_2 |
| ... | ... | ... | ... | ... | ... |
| m | x_M1 | x_M2 | ... | x_MN | Y_m |
За допомогою таблиці значень минулих спостережень можна підібрати (наприклад, методом найменших квадратів) коефіцієнти регресії, побудувавши тим самим модель.
При роботі з регресією треба дотримуватися певної обережності і обов'язково перевірити на адекватність знайдені моделі. Існують різні способи такої перевірки. Обов'язковим є статистичний аналіз залишків, тест Дарбіна-Уотсона. Корисно, як і у випадку з нейронними мережами, мати незалежний набір прикладів, на яких можна перевірити якість роботи моделі.
Методи Бокса-Дженкінса (ARIMA)
В середині 90-х років минулого століття був розроблений принципово новий і достатньо могутній клас алгоритмів для прогнозування тимчасових рядів. Велику частину роботи по дослідженню методології і перевірці моделей була проведена двома статистиками, Г.Е.П. Боксом (G.E.P. Box) і Г.М. Дженкинсом (G.M. Jenkins). З тих пір побудова подібних моделей і отримання на їх основі прогнозів іноді називатися методами Бокса-Дженкінса. В це сімейство входить декілька алгоритмів, найвідомішим і використовуваним з них є алгоритм ARIMA. Він вбудований практично в будь-який спеціалізований пакет для прогнозування. У класичному варіанті ARIMA не використовуються незалежні змінні. Моделі спираються тільки на інформацію, що міститься в передісторії прогнозованих рядів, що обмежує можливості алгоритму. В даний час в науковій літературі часто згадуються варіанти моделей ARIMA, що дозволяють враховувати незалежні змінні. У даній доповіді вони розглядатись не будуть, обмежимось тільки загальновідомим класичним варіантом. На відміну від розглянутих раніше методик прогнозування тимчасових рядів, в методології ARIMA не передбачається якої-небудь чіткої моделі для прогнозування даної тимчасової серії. Задається лише загальний клас моделей, що описують часовий ряд і що дозволяють якось виражати поточне значення змінної через її попередні значення. Потім алгоритм, підстроюючи внутрішні параметри, сам вибирає найбільш відповідну модель прогнозування. Як вже наголошувалося вище, існує ціла ієрархія моделей Бокса-Дженкінса. Логічно її можна визначити так
AR(p)+MA(q)→ARMA(p,q)→ARMA(p,q)(P,Q)→ARIMA(p,q,r)(P,Q,R)→...
AR(p) -авторегресивна модель порядку р
Модель має вигляд:
[math]Y\left( t \right)=f_{0}+f_{1}\cdot Y\left( t-1 \right)+f_{2}\cdot Y\left( t-2 \right)+...+f_{p}\cdot Y\left( t-p \right)+E\left( t \right)[/math]
де Y(t) –залежна змінна у момент часу t. [math]f_{0},f_{1},f_{2}...,f_{p}[/math] - оцінювані параметри. E(t) - помилка від впливу змінних, які не враховуються в даній моделі. Завдання полягає в тому, щоб визначити [math]f_{0},f_{1},f_{2}...,f_{p}[/math]. Їх можна оцінити різними способами. Найправильніше шукати їх через систему рівнянь Юла-Уолкера, для складання цієї системи буде потрібно розрахунок значень автокореляційної функції. Можна поступити простішим способом - порахувати їх методом найменших квадратів.
MA(q) -модель з ковзаючим середнім порядку q
Модель має вигляд:
[math]Y\left( t \right)=m+e\left( t \right)-w_{1}\cdot e\left( t-1 \right)-w_{2}\cdot e\left( t-2 \right)-...-w_{p}\cdot e\left( t-p \right)[/math]
Де Y(t) -залежна змінна у момент часу t. [math]w_{0},w_{1},w_{2}...,w_{p}[/math] - оцінювані параметри.
Авторегресійне ковзне середнє ARMA(p,q)
Під позначенням ARMA(p,q) [3] розуміється модель, p авторегресійних складових, що містить q, ковзаючих середніх.
Точніше модель ARMA(p,q) включає моделі AR(p) і MA(q):
[math]X_{t}=c+e_{t}+\sum\limits_{i=1}^{q}{\theta _{i}e_{t-i}}+\sum\limits_{i=1}^{p}{\phi _{i}X_{t-i}},[/math]
Зазвичай значення помилки [math]e_{t}[/math] вважають незалежними однаково розподіленими випадковими величинами, узятими з нормального розподілу з нульовим середнім: [math]e_{t}\sim N\left( 0,\sigma ^{2} \right),[/math] де [math]\sigma ^{2}[/math] — дисперсія. Припущення можна ослабити, але це може привести до зміни властивостей моделі. Наприклад, якщо не припускати незалежності і однакового розподілу помилок, поведінка моделі суттєво міняється.
ARIMA (p,d,q)
У завданні аналізу тимчасового ряду з складною структурою часто використовуються моделі класу ARIMA(p,d,q)[2] (авторегресійне інтегрування ковзаючого середнього - Autoregressive Integrated Moving Average) порядку (p,d,q), які моделюють різні ситуації, що зустрічаються при аналізі стаціонарних і нестаціонарних рядів. Залежно від аналізованого ряду модель ARIMA (p,d,q) може трансформуватися до авторегресійної моделі AR(p), моделі ковзного середнього MA(q) або змішаній моделі ARMA (p,q). При переході від нестаціонарного ряду до стаціонарного значення параметра d, що визначає порядок різниці, приймається рівним 0 або 1, тобто цей параметр має тільки цілочисельні значення. Зазвичай обмежуються вибором між d = 0 і d = 1. Проте з поля зору дослідників випадає ситуація, коли параметр d може приймати дробові значення.
ARFIMA(p,d,q)
Для ситуації розгляду дробових значень порядку різниці, в роботах зарубіжних учених, в першу чергу, C.W.Granger, J.R.Hosking, P.M.Robinson, R. Beran, був запропонований новий клас моделей ARFIMA(p,d,q)[2] (F: fractional - дріб), що допускає можливість нецілого параметра d і авторегресійний дріб інтегрований процес ковзного середнього. Такі ряди володіють своєю специфікою: самоподібністю, дробовою розмірністю, поволі спадаючою кореляцією. Прогнозування тимчасових рядів за допомогою моделі ARFIMA(p,d,q) відкриває ширші перспективи для підвищення точності прогнозу.
Модель вигляду ARIMA (p,d,q)(P,D,Q)S
ARIMA (p,d,q)(P,D,Q)S [1],
де: p - авторегресійні доданки;
D - різниці;
q - доданки ковзаючого середнього;
P – сезонні авторегресійні доданки;
D – сезонні різниці на інтервалі S;
Q – доданки сезонного ковзаючого середнього
Метод "Гусениці" SSA
Метод SSALRF[6,7]
Метод “Гусеніца”-SSA може бути використаний для різних загальних завдань дослідження тимчасових рядів, зокрема - для виділення сигналу і знаходження його ЛРФ. При його використанні по ряду [math]F_{N}[/math] будується траєкторна матриця X заданого розміру L x K, 1 < L < N.
K = N – L + 1 (L називається довжиною вікна), обчислюються власні числа [math]\left\{ \lambda _{i} \right\}_{i=1}^{L},[/math] власні [math]\left\{ \lambda _{i} \right\}_{i=1}^{L},[/math]і факторні [math]\left\{ V_{i} \right\}_{i=1}^{L}[/math] вектора матриці [math]XX^{T}[/math], формуючи сингулярне розкладання [math]X=\sum\limits_{i}{\sqrt{\lambda _{i}}U_{i}V_{i}^{T}}[/math]. Набір [math]\left( \sqrt{\lambda _{i}}U_{i}V_{i} \right)[/math] називається сингулярною трійкою. Ряду зіставляється траєкторний простір, аддитивній складовій ряду при виконанні умов роздільності відповідає власний траєкторний підпростір в цьому просторі.
В умовах наближеної роздільності метод дозволяє знайти підпростір близьке до траєкторного простору даної аддитивної складової.
Опишемо алгоритм методу SSALRF, в нім можна виділити наступну послідовність кроків.
Алгоритм [5]
- Вибір довжини вікна L і побудова траєкторної матриці [math]X\in \mathbb{R}^{L\times K}[/math] по ряду [math]F_{N}[/math];
- Сингулярне розкладання траєкторної матриці [math]X=\sum\limits_{i}{\sqrt{\lambda _{i}}U_{i}V_{i}^{T}}[/math] ;
- Вибір сингулярних трійок, відповідних сигналу [math]S_{N}[/math];
- Побудова по власних векторах вибраних сингулярних трійок наближеної ЛРФ сигналу порядку L – 1;
- Знаходження кореня характеристичного полінома цієї ЛРФ;
- Пошук головного кореня серед всієї безлічі коренів;
- Отримання наближеною мінімальною ЛРФ (порядка 2) сигналу по головному кореню.
Перелік використаних джерел
- http://ipu-conf.ru/kmu/sbornik_VMKPU2008.pdf (лютий 2010)
- http://www.guap.ru/guap/main/avtoref_krichevsky.doc (лютий 2010)
- http://www.machinelearning.ru/wiki/index.php?title= Авторегрессионное_скользящее_среднее (лютий 2010)
- http://www.neuroproject.ru/forecasting_tutorial.php#mlp Методы прогнозирования (лютий 2010)
- http://www.pdmi.ras.ru/~theo/autossa/files/SSAvsREGR--paper.pdf Метод SSALRF (лютий 2010)
- http://www.nsu.ru/ef/tsy/ecmr/Forum/topic77.htm Конференция по эконометрике » AR, ARMA, ARIMA, FARIMA (лютий 2010)
- Метод_Хольта
- Методи прогнозування (eng.)

- Студент: Користувач:Hotcoffe
- Виступ відбувся: 30 лютого 2010
- Тема: Методи прогнозування.