Лінія течії
Зміст
Визначення
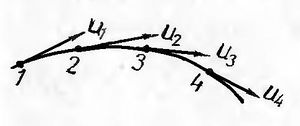
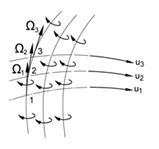
Лінії течії – лінії, дотичні до яких у кожній точці співпадають за напрямом з векторами швидкостей частинок рідини, а густина проведення ліній течії (відношення числа ліній [math]\triangle\[/math]N до величини перпендикулярної до них площі [math]\triangle\[/math]S, через яку вони проходять) пропорційна величині швидкості у даній точці. Сукупність ліній течії називають спектром течії. Спектри дають змогу розглядати різноманітні гідравлічні явища з якісного боку.
Пояснення явища
Наочне уявлення про миттєву картину течії рідини дають так звані лінії течії. Щоб усвідомити зміст поняття лінії течії, уявимо собі, що в рідині, яка перебуває в русі, проведено певну криву, дотичні до якої у довільній точці в дану мить часу збігаються з напрямом вектора швидкості. Тоді така крива, яку називатимемо лінією течії, дає змогу визначити напрямок миттєвих швидкостей в усіх точках цієї кривої.Лінії течії як на поверхні, так і всередині рухомої рідини легко зробити видимими. Якщо ввести в рідину різні нерозчинні речовини, які можуть рухатися разом з рідиною, то вигляд ліній течії змінюється зі зміною розподілу швидкостей. В умовах стаціонарного руху лінії течії не змінюють свого обрису в потоці, отже вони збігаються з траєкторіями. При нестаціонарному русі дотичними по лінії течії є швидкості різних частинок, тому в цьому випадку лінії і траєкторії не суміщаються.
Рівняння лінї течії
Можна сказати, що лінії течії аналогічні силовим лініям силових полів.
Якщо ux, uy, uz не рівні нулю, то рух називають просторовим, якщо одна з компонент рівна нулю, то одержуємо плоский рух, якщо дві компоненти рівні нулю, то одержуємо одновимірний рух.
Якщо за час dt частинка рідини пройде за напрямком лінії течії шлях dl з компонентами на координатних осях, рівним dx, dy, dz, то складові цієї швидкості становитимуть:
[math]u_x=dx/dt; u_y=dy/dt; u_z=dz/dt.[/math]
а тому
[math]dx/u_x=dy/u_y=dz/u_z.[/math] (1.1)
Система рівнянь (1.1) є рівнянням лінії течії. Для плоского руху відповідно можна записати
[math]dx/u_x=dy/u_y=dt[/math]
або
[math]dx/f_1(x,y,t)=dy/f_2(x,y,t)[/math] (1.2)
Рівняння (1.2) є рівнянням лінії течії плоского потоку.
Струминна модель потоку
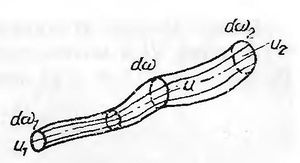
Уявимо собі тепер, що в рухомій рідині виділено замкнений контур з елементакрною площею поперечного перерізу [math]dw[/math].Поверхню, утворену лініями течії, проведеними через усі точки цього замкненого контуру, називають трубкою течії, а масу рідини що протікає всередині трубки течії, - елементарною струминкою. Струминна модель потоку введена Л.Ейлером.
Поверхню нормальну в кожній точці до лінії течії називають живим перетином струминки. У загальному випадку поверхня живого перетину є криволінійною, перетворюючись у плоску при паралельно-струминному потоці. При вивченні багатьох гідравлічних явищ трапляються випадки, коли струминки не паралельні одна одній, але кривина струминок невелика і кут розходження між ними дуже малий. Такий рух називають плавно-змінним.
Слід підкреслити, що при стаціонарному русі трубка течії, утворена лініями течії, не змінюється в часі та є немовби непроникною трубкою, в якій рідина тече як в трубці з твердими стінками що обмежують її вміст. Рідина з трубки течії не витікає в сторону і не додається до неї, тому що у всіх точках струминки швидкість спрямована вздовж лінії течії.В елементарній струминці швидкості в усіх точках одного й того ж поперечного перерізу можна приймати однаковими і рівними місцевими швидкостями.
Для врахування умов руху рідини залежно від форми і розмірів живого перерізу в гідравліці використовують поняття змоченого периметра і гідравлічного радіуса.
Змоченим периметром χ називають ту частину периметра живого перерізу, по якій рідина стикається зі стінками, що її обмежують.
Гідравлічним радіусом R називають відношення площі живого перерізу до змоченого периметра
[math]R=w/x[/math] (1.3)
Окрім поступального руху рідина може здійснювати обертальний рух та рух деформації. Потік рідини, що здійснює обертальний рух називають вихровим. Вихровий рух характеризується кутовою швидкістю обертання елементарної рідкої частки.
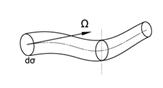
Представивши кутову швидкість частки вектором можна графічно представити усі подальші у часі положення осі обертання частки. Лінію, у кожній точці якої вектор вихору збігається за напрямом з дотичною до неї, називають вихровою лінією.
Вихрові лінії, проведені через кожну точку нескінченно малого контуру утворюють вихрову нитку. При контурі кінцевого розміру одержуємо вихровий шнур.
Рівняння вихрової лінії мають вигляд
[math]dx/\Omega_x=dy/\Omega_y=dz/\Omega_z[/math] (1.4)
де [math]\Omega_x=2w_x,\Omega_y=2w_y,\Omega_z=2w_z[/math] – компоненти вихору швидкості, що рівні подвоєним за значенням компонентам вектору кутової швидкості.
Висновки
Елементарна струминка є наочним кінематичним образом, який істотно полегшує вивчення руху рідини і покладений в основу так званої струминної моделі руху рідини. Відповідно до цієї моделі, введеної в гідравліку ще в період формування її як науки, простір, зайнятий рухомою рідиною, умовно розглядають як сукупність цілого ряду елементарних струминок, що протікають через достатньо велику площу, утворює потік рідини.
Струминна модель течії сьогодні є однією з основних моделей потоку рідини.
Література
Левицкий Б. Ф., Лещій Н. П. Гідравліка. Загальний курс : підручник / Б. Ф. Левицький., Лещій Н. П. – Львів : Світ, 1994. – 264 с.
І.І. Науменко, О.І. Токар, Л.О. Токар. Інтерактивний комплекс навчально-методичного забезпечення дисципліни “Гідрогазодинаміка”. Навчально-методичний комплекс. – Рівне: НУВГП, 2007. – 118 с.