Критерій узгодженості Стьюдента

Критерій узгодженості Стьюдента - статистичний критерій згоди, заснований на порівнянні з розподілом Стьюдента (t-розподілом). Розроблений англійським хіміком-харчовиком Вільямом Госсетом (псевдонім — Стьюдент). Для практичного вивчення робочих процесів закон нормального розподілу часто не підходить, хоча існують підстави вважати, що змінна розподілена нормально. Це пов'язано з тим, що як аргумент до нормального розподілу входять математичне сподівання $M$ та СКВ $\sigma$, які звичайно залишаються невідомими, тому його замінюють розподілом Стьюдента, який застосовується для нормально розподіленої послідовності.

Закон розподілу

$t=\frac{x_0}{\sqrt{{m^{-1}}*{\left (x_1^2+x_2^2+...+x_m^2 \right)}}$,

де $x_0,x_1,...,x_m$ - взаємно незалежні нормально розподілені випадкові величини з $M=0$ і довільними дисперсіями $D$.

Закон Стьюдента свідчить, що $p(t)$ залежить від числа ступенів вільності $f=N-1$ та величини $S$. Критерій $t$ може набувати різних форм, а $t$-розподіл лежить в основі теорії малих вибірок, яка відіграла значну роль в плануванні експериментів.

Криві розподілу

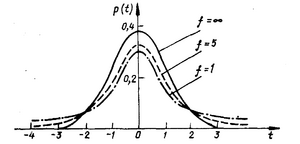
Криві розподілу

Максимуми частоти нормального та $t$-розподілів лежать при одному й тому ж значенні абсциси. Проте на відміну від нормального розподілу висота і ширина кривих нормованого $t$-розподілу залежать від числа ступенів вільності $f$ відповідного СКВ. Чим менше $f$, тим більш похилий хід має крива при одному й тому ж значенні $S$. При $f \to \ \infty$ $t$-розподіл переходить у нормальний розподіл. Відповідно до цього для ходу кривої, який залежить від $f$, межі інтегрування $p$ при заданій надійній імовірності $\gamma$ все більше віддаляються від середнього значення зі зменшенням числа ступенів вільності $f$. Так, для $\gamma$ = 0,95 виміряні значення не лежать в області $x$ ± 25. Цей інтервал стає тим ширшим, чим менше вимірювань було проведено.

Застосування

Як свідчить структура відношення Стьюдента, $t$-розподіл використовується при розв'язанні першої групи задач(задачі порівняння середнього значення виміряного ряду змінних із заданими значеннями або з середнім іншого ряду), проте його також застосовують при виявленні грубих помилок та ін.

Порівняння із заданим значенням

Нульова гіпотеза $H_0:\; \bar x = \mu$ (вибіркове середнє рівне заданому числу $\mu$).

Критерій (при рівні значимості $\alpha$):

• проти альтернативи $H_1:\; \bar x \neq \mu$

якщо $|t| \gt t_{\alpha/2}$, то нульова гіпотеза відхиляється;

• проти альтернативи $H'_1:\; \bar x \lt \mu$

якщо $t \lt t_{\alpha}$ , то нульова гіпотеза відхиляється;

• проти альтернативи H_1:\; \bar x > \mu

якщо $t \gt t_{1-\alpha}$ , то нульова гіпотеза відхиляється;

де $t_{\alpha}$ є $\alpha$-квантилем розподілу Стьюдента з m-1 ступенями свободи.