Коефіцієнт Дарсі
Коефіцієнт Дарсі (коефіцієнт гідравлічного тертя) [math]\lambda[/math] - безрозмірна величина, що характеризує співвідношення сил тертя і інерції і саме її визначення, і є предметом гідравлічного розрахунку трубопроводу. Втрати на тертя обумовлені в'язкісним тертям шарів рідини, що рухаються усередині потоку з різною швидкістю, а також тертям об внутрішню поверхню труби шарів рідини, що рухаються в безпосередній близькості від неї.
Експериментально встановлено,що гідравлічний коефіцієнт тертя, як правило залежить від режиму руху рідини,який характеризується числом Рейнольдса ([math]Re[/math]) і внутрішньої поверхні трубопроводу, який характеризується відносною шорсткістю ([math]\varepsilon[/math]). Вплив цих факторів на величину [math]\lambda[/math] при ламінарному і турбулентному режимах проявляється по-різному.
При визначенні [math]\lambda[/math] враховується не абсолютна шорсткість, а її відношення до діаметру (або радіусу) труби, тобто відносна шорсткість. Це обумовлено тим, що одна і та ж абсолютна шорсткість надає більший вплив на опір руху в трубопроводі меншого діаметру. Запропоновано велику кількість емпіричних і напівемпіричних формул для визначення коефіцієнта гідравлічного тертя [math]\lambda[/math], що враховують особливості перебігу при турбулентному режимі. Ці особливості в кінцевому підсумку позначаються на залежності колійних втрат від середньої швидкості течії.
Зміст
Історична довідка
Анрі Філібер Гаспар Дарсі (фр. Henry Philibert Gaspard Darcy, 10 червня 1803, Діжон, - 2 січня 1858, Париж) - французький інженер-гідравлік, котрий обгрунтував закон Дарсі (1856), що зв'язує швидкість фільтрації рідини в пористому середовищі з градієнтом тиску: «Очевидно, для піску однієї якості витрата, що пропускається ним прямо пропорційна натиску і обернено пропорційна товщині фільтруючого шару (ґрунту)». Ім'ям Дарсі названа одиниця вимірювання проникності пористого середовища.
Як член Корпорації, він побудував унікальну водопровідну систему подачі води під тиском в Діжоні після невдалої спроби добувати чисту прісну воду шляхом буріння свердловин. Система постачала воду з продуктивністю 7000 літрів на хвилину з джерела Rosoir Spring з відстані 12,7 км по закритому водопроводу у водосховища біля міста, звідки потім подавалася в міську трубопровідну мережу загальною довжиною 28,000 метрів під тиском. Система була повністю закрита і у своїй роботі використовувала лише сили тяжіння та не вимагала фільтрів чи насосів. Він також брав участь у багатьох інших громадських заходах міста Діжон і регіону, а також у виробленні політики благоустрою міста Діжон.
Він модифікував формула Проні для розрахунку втрат напору на тертя, яке після подальшої модифікації Юліусом Вейсбахом, стало відомим рівнянням Дарсі-Вейсбаха, яке використовується і сьогодні.
Помер від пневмонії під час поїздки у Париж в 1858 році і був похований у Діжоні.
Формула Дарсі-Вейсбаха
Для круглих труб сталого перерізу втрати напору на тертя визначають за формулою Дарсі:
[math]\xi = \lambda \cdot \frac{L}{D},[/math]
де [math]\lambda[/math] — коефіцієнт гідравлічного тертя по довжині (коефіцієнт Дарсі).
Тоді формула Дарсі набуває вигляду:
[math]\Delta h = \lambda \cdot \frac{L}{D} \cdot \frac{V^2}{2g}[/math]
де [math]L[/math] і [math]D[/math] — відповідно довжина та діаметр трубопроводу; [math]V[/math] — середня швидкість руху рідини; [math]\lambda[/math] — коефіцієнт гідравлічного тертя, який залежить від в'язкості, яка входить до числа Рейнольдса та відносної шорсткості стінок труби .
або для втрати тиску:
[math]\Delta P = \lambda \cdot \frac{L}{D} \cdot \frac{V^2}{2} \cdot \rho[/math]
Якщо визначаються втрати на тертя для труби не круглого поперечного перерізу, то за [math]D[/math] береться гідравлічний діаметр.
Слід відзначити, що втрати напору на гідравлічних опорах не завжди пропорційні швидкісному напору.
Визначення гідравлічного коефіцієнта тертя по довжині
Коефіцієнт [math]\lambda[/math] визначається по різному для різних випадків.
При ламінарному режимі, тобто [math]\operatorname{Re}=\frac{\vartheta \cdot d}{\nu }\,\le \,2300[/math] ([math]\nu[/math] - кінематичний коефіцієнт в'язкості) стан поверхності стінки не впливає на опір рідини і [math]\lambda=f(Re)[/math]. Значення коефіцієнта [math]\lambda[/math] в цьому випадку визначається з теоретичною формулою Пуазейля:
[math]\lambda \text{=}\frac{64}{\operatorname{Re}}[/math]
де ([math]Re[/math]) — число Рейнольдса.
Іноді для гнучких труб у розрахунках приймають:
[math]\lambda \text{=}\frac{68}{\operatorname{Re}}[/math]
Турбулентний режим течії характеризується інтенсивним перемішуванням рідини як у поперечному (по перерізу потоку), так і в поздовжньому (по довжині потоку) напрямках.Проте в діапазоні чисел Рейнольдса [math]2320\,\le \,\operatorname{Re}\,\le \,{{10}^{5}}[/math] безпосередньо поблизу стінок трубопроводу існує шар рухомої рідини, перебіг в якому зберігається ламінарним.
Для турбулентної течії існують складніші залежності. Одна з найпоширеніших формул — це формула Блазіуса:
[math]\lambda \text{=}\frac{0,316}{^{4}\sqrt{\operatorname{Re}}}[/math]
Визначення коефіцієнта для місцевих опорів
Для кожного виду місцевих опорів існують свої залежності для визначення коефіцієнта [math]\xi\[/math]. До числа найбільш поширених місцевих опорів відносяться раптове розширення труби, раптове звуження труби і поворот труби.
1. При раптовому розширенні труби:
[math]\xi = \left( 1 - \frac{S_1}{S_2} \right)^2 ,[/math]
де [math]S_1[/math] і [math]S_2[/math] - площі поперечного перерізу труби, відповідно перед розширенням і після нього.
2. При раптовому звуженні труби коефіцієнт місцевого опору визначається за формулою:
[math]\xi = \frac{1 -S_2/S_1}{2},[/math]
де [math]S_1[/math] і [math]S_2[/math] - площі поперечного перерізу труби, відповідно, перед звуженням і після нього.
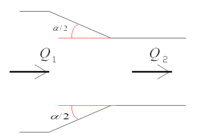
3. При поступовому звуженні труби (конфузор):
[math]\xi =\frac{\lambda_T}{8\sin{\alpha/2}} \left( 1-\frac{1}{n^2} \right)[/math],
де - [math]n =\frac{S_1}{S_2}[/math] ступінь звуження; [math]\lambda_T[/math] - коефіцієнт втрат на тертя по довжині при турбулентному режимі.
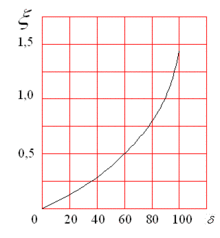
4. При різкому (без закруглення) повороті труби (коліно) коефіцієнт місцевого опору визначається за графічним залежностям (рис. 2).
Опис установки
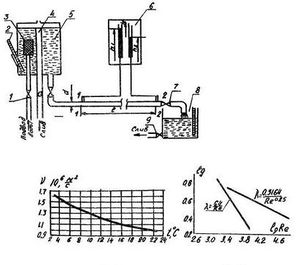
Принципова схема експериментальної установки, що використовується для визначення коефіцієнта гідравлічного тертя [math]\lambda[/math] наведена на рис. 3.
Експериментальна ділянка трубопроводу круглого перетину довжиною [math]L[/math] приєднана до напірного баку 5, в який з водогону через вентиль 1 і заспокійливу сітку 3 безперервно подається вода. Надлишки води з бака зливаються через переливну трубу 4. Тому в баці може підтримуватися постійний рівень. Витрата води через експериментальну ділянку регулюється вентилем 7 (вентиль на вході в експериментальну ділянку повністю відкритий під час всього експерименту). Після проходження експериментальної ділянки вода зливається в мірний бак 8, на вході з якого є кран 9. Для вимірювання температури води встановлений термометр 2. Установка оснащена п'єзометричним щитом 6, на якому встановлені пєзометри для вимірювання втрат по довжині.
Найбільш часто вживані формули для обчислення значення коефіцієнта [math]\lambda[/math]
Визначення [math]\lambda[/math] за наведеними та іншими формулами полегшується використанням таблиць і номограм, що містяться у навчальних та довідкових посібниках.
При проведенні даної роботи розглядаються режими течії в гідравлічно гладких трубах.
Зона опору, режим:
1. Ламінарний:
Межі зони: [math]\operatorname{Re}\lt 2300[/math]
Розрахункова формула: [math]\lambda \text{=}\frac{64}{\operatorname{Re}}[/math] - ф. Пуазейля
Залежність втрат напору від швидкості: [math]h_i\sim\;v[/math]
2. Зона гладкостінного опору:
а) Межі зони: [math]2320\,\le \,\operatorname{Re}\,\le \,{{10}^{5}}[/math]
Розрахункова формула: [math]\lambda \text{=}\frac{0,316}{^{4}\sqrt{\operatorname{Re}}}[/math] - ф. Блазіуса
Залежність втрат напору від швидкості: [math]h_i\sim\;v^{1,75}[/math]
б) Межі зони: [math]4000\,\le \,\operatorname{Re}\,\le \,{3\cdot{10}^{6}}[/math]
Розрахункова формула: [math]\lambda = \frac{1}{(1,8Lg(Re)-1,5)^{2}}[/math] - ф. Конакова
3. Зона доквадратичного опору:
а) Межі зони: [math]20\cdot\frac{d}{\Delta_\epsilon}\le \;\operatorname{Re}\le \;{500\cdot \frac{d}{\Delta_\epsilon}}[/math]
Розрахункова формула: [math]\lambda = \frac{1}{(2Lg(\frac{2,51}{Re}))}[/math] - ф. Кольбрука Уайта
Залежність втрат напору від швидкості: [math]h_i\sim\;v^{\frac{1,75}{2}}[/math]
б) Межі зони: [math]20\cdot\frac{d}{\Delta_\epsilon}\le \;\operatorname{Re}\le \;{500\cdot \frac{d}{\Delta_\epsilon}}[/math]
Розрахункова формула: [math]\lambda \approx \; 0,11{(\frac{\Delta_\epsilon}{d}+\frac{68}{Re})^{0,25}}[/math] - ф. Альтшуль
4. Зона квадратичного опору:
а) Межі зони: [math]\operatorname{Re}\ge \;{500\cdot \frac{d}{\Delta_\epsilon}}[/math]
Розрахункова формула: [math]\lambda = \frac{1}{{(2Lg(\frac{3,7\cdot d}{\Delta_\epsilon}))^{2}}}[/math] - ф. Прандтля-Нікурадзе
Залежність втрат напору від швидкості: [math]h_i\sim\;v^{2}[/math]
б) Межі зони: [math]\operatorname{Re}\ge \;{500\cdot \frac{d}{\Delta_\epsilon}}[/math]
Розрахункова формула: [math]\lambda = 0,11{(\frac{\Delta_\epsilon}{d})^{0,25}}[/math] - ф. Шіфрінсона
Література
Левицький Б.Ф., Лещій Н.П. Гідравліка.Загальний курс - Львів: Cвіт,1994.-264с.
О.М. Коваленко,Т.О. Шевченко Інженерна гідравліка. Розділ I. Рух рідини в закритих руслах – Харків: ХНАМГ, 2007.-76 с
Идельчик И.Е. Справочник по гидравлическим сопротивлениям. – М.: Машиностроение, 1975. – 559 с.
Дробинс В. Ф. Гидравлика и гидравлические машины. – М.: Просвещение, 1982.
Установка для изучения потерь напора при турбулентном установившемся движении (тип ГВ5). – Одесоргнаучкомплектснаб. – 39 с.