Статистичні критерії згоди
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
| {{{img}}} | ||
| Імя | Тарас | |
| Прізвище | Івасюк | |
| По-батькові | Анатолійович | |
| Факультет | ФІС | |
| Група | СН-51 | |
| Залікова книжка | СН-10-055 | |
Зміст
Статистичні критерії згоди
До перевірки тієї чи іншої статистичної гіпотези доціль¬но підходити з різних теоретичних позицій. Кожна позиція грунтується на розподілі первинних або обчислених даних, які відрізняються від нормального розподілу. Це зумовлено обмеженим числом вимірювань або додатковими умовами при обробці дослідних даних. Характеристикою кожного розподілу є набір чисел, заздалегідь протабульованих. При перевірці гіпотези з дослідних даних складається число за тим же правилом, що й наведені в таблиці числа, і порівнюється з табличним числом. Гіпотеза визнається або відхиляється залежно від згоди дослідних і табличних чисел, тому останні називаються критеріями згоди. Як і в інших галузях науки, наприклад в теорії подібності, статистичні критерії — величини звичайно безрозмірні. Нехай х — нормально розподілена випадкова змінна. При відомому СКВ висувається нуль-гіпотеза [math]M(x)=m_0[/math] або [math]M(x)-m_0=0[/math], тобто середнє значення, або математичне сподівання М(х), генеральної сукупності, оцінюване на основі випадкової вибірки, не відрізняється від заданого значення [math]m_o[/math]. Альтернативна гіпотеза [math]H_A[/math] протилежна нуль-гіпотезі, тобто [math]M(x)\ne m_0[/math] або [math]M(x)-m_0\ne 0[/math]. Як критерій ви¬користовується відношення різниці порівнюваних величин [math]\bar{x}-m_0[/math] до статистичної помилки [math]S/\sqrt N[/math] розрахункової величини [math]\bar x[/math]:
де N — обсяг вибірки; [math]\bar{x}[/math] — оцінка математичного сподівання М(х) генеральної сукупності.
Статистична помилка
Статистична помилка, або помилка репрезентативності (відтворюваності)— це відхилення даного вибіркового показника від його справжнього значення в генеральній сукупності. Для вибіркового середнього це значення в [math]\sqrt{N}[/math] разів менше, ніж СКВ S. Згідно з теорією статистичної обробки обмеженого числа дослідних даних імовірність значення Z розподілена за законом Стьюдента:
де G — гама-функція, табличні значення якої можна знайти в довідниках з математики або статистики. Залежно від параметрів вибірки значення Z відрізняється від нуля, як міра відхилення вважається абсолютне значення |Z|. За прийнятим рівнем значущості [math]\alpha[/math] можна визначити таке критичне значення [math]Z_kp[/math], що при вірній нуль-гіпотезі справедлива нерівність [math]|Z|\ge Z_kp[/math] тобто [math]p(|Z|\ge Z_kp)=\alpha[/math].
Якщо число Z обчислене за вибіркою, задовольняє нерівність [math]|Z|\lt Z_kp[/math] то вважатимемо, що відхилення Z від 0 можна розглядати як випадкове. Тоді говорять, що нуль-гіпотеза не відхиляється на основі вибірки або немає підстав для її відхилення.
Якщо [math]|Z|\ge Z_kp[/math], то при справедливій нуль-гіпотезі таке відхилення можливе але малоімовірне. Тоді вважають більш імовірним, що нуль-гіпотеза невірна, і її відхиляють. При аналізі рішень слід мати на увазі обидва можливі типи помилок. Співвідношення імовірностей [math]\alpha[/math] i [math]\beta[/math] проілюстровано на рис.1, де наведено графіки розподілу імовірностей при
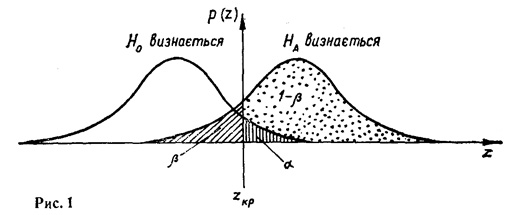
порівнянні арифметичних середніх, здобутих з двох вибірок: лівий зображає нуль-гіпотезу [math]H_0[/math], правий альтернативну гіпотезу [math]H_A[/math]. Залежно від значення обчисленого на підставі вибіркових даних Z і його положення по відношенню до [math]Z_kp[/math] можливі два рішення: якщо значення її дорівнює або перевищує [math]Z_kp[/math], то нуль-гіпотеза відхиляється і визнається альтернативна гіпотеза; якщо [math]Z\lt Z_kp[/math], то немає підстав для відхилення [math]H_0[/math] тобто вона підтверджується .
При одному й тому ж розташуванні графіків розподілу імовірностей зі зменшенням імовірності помилки [math]\alpha[/math] значення [math]\beta[/math] зростає. Імовірність [math]\beta[/math] визнати невірну нуль-гіпотезу залежить, зокрема, від:
обсягу вибірки (чим більша вибірка, тим надійніше при даному рівні значущості [math]\alpha[/math] буде встановлена аналізована відмінність між статистичними характеристиками);
ступеня відмінності між цими характеристиками;
потужності критерію.
Потужність критерію
Потужність критерію - це імовірність відхилити нульову гіпотезу [math]H_0[/math], коли вірна гіпотеза [math]H_A[/math], тобто [math]p=1-\beta[/math]. Чим менша при заданому [math]\alpha[/math] імовірність [math]\beta[/math], тим краще критерій розділяє гіпотези [math]H_0[/math] та [math]H_A[/math].
Критерій називається потужним, коли він порівняно з іншими можливими критеріями при заданому [math]\alpha[/math] показує вищу дискримінуючу здатність, тобто здатність до розділення гіпотез. За потужністю, критерії згоди діляться на дві великі групи: параметричні та непараметричні. До параметричних належать критерії, побудовані за допомогою основних параметрів (числових оцінок) вибіркової сукупності М та \sigma або [math]\bar x[/math] та S. Ці критерії застосовуються лише тоді, коли генеральна сукупність, з якої взято одну або кілька вибірок, розподілена нормально, і за умови рівності основних параметрів, тобто [math]\bar x_1 - \bar x_2[/math] та [math]S_1-S_2[/math].
Непараметричні критерії згоди є функціями лише змінних даної сукупності (вибірки) з їх частотами і не потребують знання типу розподілу генеральної сукупності. Тому їх застосовують при перевірці властивостей гіпотетичного розподілу. Параметричні критерії мають сильнішу дискримінуючу (роздільну) здатність, більшу потужність порівняно з непараметричними. Коли досліджувана сукупність розподіляється за нормальним законом або не дуже відхиляється від нього, слід надавати перевагу таким критеріям.
Потужність критерію збільшується при збільшенні обсягу вибірки. Якщо ж обсяг вибірки малий і збільшити його не вдається, то треба брати невисокий рівень значущості, оскільки і мала вибірка, і високий рівень значущості призводить до небажаного зменшення потужності критерію. Слід пам'ятати про те, що при зворотному переході до вищого рівня значущості обчислене значення Z може з області відхилення нульової гіпотези перейти в область її визнання. Наприклад, якщо Z було справа від [math]Z_kp[/math], то з підвищенням [math]\gamma[/math] воно може з'явитися зліва від [math]Z_kp[/math] (див. рисунок 1).
При плануванні та реалізації експериментів задаються імовірністю тільки помилки першого роду. Далі, рекомендуючи той чи інший критерій згоди, вибиратимемо найпотужніший з можливих критеріїв, тобто будемо враховувати також помилки другого роду. Слід пам'ятати, що, задаючись занадто високим рівнем значущості, ми знижуємо [math]\alpha[/math] і разом з тим підвищуємо [math]\beta[/math] тому бажано обмежуватися 5%-м рівнем значущості.
Ступінь вільності
Поняття статистичного критерію тісно пов'язане з поняттям ступеня вільності. Для більшості критеріїв ступінь вільності є аргументом. Величина N—1, що стоїть у знаменнику формул для обчислення СКВ, є числом ступенів вільності. Під числом ступенів вільності розуміють число змінних, значення яких задаються довільно. Іншими словами, це є загальне число змінних мінус число лінійних зв'язків, накладених на систему, що вивчається. Так, при розрахунку СКВ за N експериментальними даними Існує лише один зв'язок (обмеження), обумовлений розрахунком середнього арифметичного, тобто число ступенів вільності f=N-1.
Дійсно, якщо за вибіркою з п'яти даних [math]x_1, x_2, ..., x_5[/math] утворено середнє [math]\bar{x}=20[/math], то чотири значення [math]x_i[/math] можуть бути якими завгодно, наприклад 10, 15, 21, 16 або 19, 25, 13, ЗО, але одне — [math]x_5[/math] у першому випадку має бути [math]x_5=20*5-(10 + 15 + 21 + 16) = 38[/math], а в другому [math]x_5 = 20*5-(19 + 25 + 13 + ЗО) = 13[/math].
Отже, під числом ступенів вільності будемо розуміти різницю між числом дослідів та числом характеристик, які визначаються за утвореними даними незалежно одне від одного.
Список використаних джерел
1. Математичне планування експериментів в АПК / В. О. Аністратенко, В. Г. Федоров.-К.:Вища школа,1993.-374с.