Ефект Коанда
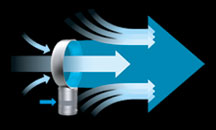
Ефект Коанда-ефект був відкритий у 1932 році румунським вченим Анрі Коандом.Ефект заключається у тому що струя рідини чи газу "прилипає" до поверхні яку обтікає.Ніякого прилипання насправді, звичайно ж, немає. Пояснюється все тієї ж різницею тисків між шарами повітря, яка є причиною і багатьох інших цікавих явищ в повітрі і воді. А в аеродинаміці давно користуються моделлю, заснованої на шарах повітря, що мають однакову швидкість руху.
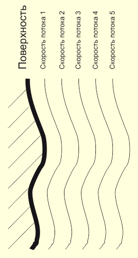
Візьмемо якийсь прилад, датчик якого має розмір вістря голки, і який вміє вимірювати швидкість водного або повітряного потоку. Цим датчиком-вістрям почнемо перетинати потік поперек, відстежуючи зміну швидкості повітря на різній відстані від обтічної поверхні на цьому маленькому ділянці, розмірами з вістрі голки. І, проводячи ці виміри, ми зауважимо, що швидкість потоку ніколи не змінюється миттєво на велику величину.
Це один з базових ефектів аеро-та гідродинаміки. Знаючи це властивість, ми можемо моделювати, тобто, математично розраховувати поведінку потоку. Винахідник або розробник може промоделювати поведінку майбутнього устрою до побудови прототипу чи моделі. Тобто, до дорогих випробувань.
Що ж відбувається з потоками при обтіканні поверхні? Причина, швидше за все, в тому, що тертя між твердою поверхнею і граничними до неї шарами потоку менше, ніж між окремими шарами потоку повітря. Крім того, десь на досить великій відстані від поверхні обов'язково з'явиться шар з майже нульовою швидкістю течії щодо розглянутої твердої поверхні.
Загалом, швидкість шарів потоку біля твердої поверхні вище, ніж на деякому віддаленні від поверхні. А ми пам'ятаємо про один з найважливіших законів в аеродинаміці - закон Бернуллі. Тобто, з боку більш повільних верств повітряний потік відчуває поперечний тиск в бік більш швидких шарів. І, весь потік відхиляється. Тобто, в разі ефекту Коанда, відхиляється в бік твердої поверхні, яка його обмежує.
Опис
Струмінь повітря може бути вільним(обмеженим навколишнім середовищем),або обмеженим(стиснутими обмеженими перепонами зі всіх сторін),або налягаючим. Налягаючий струмінь- це напівобмежений струмінь,і він завжди розвивається тільки вздовж поверхні перепони.Дальність розповсюдження налягаючого струменю збільшується приблизно в 1,2 рази у порівнянні із стиснутим струменем.Тобто струмінь що налягає на поток чи іншу поверхню, має більшу далекобійність при подальших однакових умовах ніж не налягаючий струмінь.
Це - один з базових ефектів аеро-та гідродинаміки. Знаючи цю властивість, ми можемо моделювати, тобто, математично розраховувати поведінку потоку. Винахідник або розробник може промоделювати поведінку майбутнього устрою до побудови прототипу чи моделі. Що ж відбувається з потоками при обтіканні поверхні? Причина, швидше за все, в тому, що тертя між твердою поверхнею і граничними до неї шарами потоку менше, ніж між окремими шарами потоку повітря. Крім того, десь на досить великій відстані від поверхні обов'язково з'явиться шар з майже нульовою швидкістю течії щодо розглянутої твердої поверхні.
Загалом, швидкість шарів потоку біля твердої поверхні вище, ніж на деякому віддаленні від поверхні. А ми пам'ятаємо про один з найважливіших законів в аеродинаміці - закон Бернуллі, за яким більш повільні шари повітря утворюють більший поперечний опір , ніж шари, які рухаються швидше. Тобто, з боку більш повільних шарів повітряний потік приймає поперечний тиск в бік більш швидких шарів. І, весь потік відхиляється. Тобто, в разі ефекту Коанда, відхиляється в бік твердої поверхні, яка його обмежує.
Застосування
Цей ефект застосовують в кондиціонерах для створення ефекту прилипання струменя повітря до стелі для кращого циркулювання повітря в приміщенні.
З 1940 по 1970 американці експериментували із застосуванням ефекту Коанда в створенні літальних апаратів. Ефект Коанда застосовується в технології NOTAR[1]
З використанням ефекту Коанда для збільшення підйомної сили крила, за рахунок його обдування реактивним струменем від двигуна літака, було побудовано кілька проектів літаків. Такі, як американські експериментальні QSRA і досвідчений військово-транспортний Boeing YC-14, і радянські військово-транспортні літаки з укороченим зльотом і посадкою Ан-72 і Ан-74.
Джеймс Дайсон з його інженерами, коли створювали сушарку для рук, звернули увагу, що дуже багато повітря засмоктується в отвір для рук. Вони спантеличені і створили вентилятор без зовнішнього гвинта. Потік повітря 20 літрів в секунду зі швидкістю 88 км / год виходить з вузької щілини 1.3 мм. Він захоплює зовнішнє повітря, в 15 разів перевершуючи за обсягом і викидається через щілину, і гальмує до 35 км / год. І все це забезпечується 40-ватним електромотором!
Отже, ефект Коанда часто у винахідницькій практиці використовується для засмоктування додаткової маси повітря не через вентилятор, а залученням швидкісного потоку. Це вважається більш ефективним.
Приклад для розрахунку
Розглянемо виникнення цього ефекту при взаємодії рідини чи газу з тілом напівсферичної форми, що знаходяться на кінці круглого циліндра. Для визначення величини рушійної сили необхідно задатися певними конструктивними співвідношеннями деяких розмірів і формою потоку, оточуючого півсферу. Припустимо, що оточуючий потік теж буде мати сферичну форму тільки з іншим радіусом, який позначимо через L і центр якого буде зміщений щодо центру півсфери О на величину. Відбивна пластина повинна також мати сферичну поверхню радіуса L, обмежуватися колом радіуса і перебувати на певній відстані від півсфери радіуса R. Зазор D між відбивною пластиною і тілом буде збільшуватися зі збільшенням кута j і на краях пластини (при ф=ф0 ) буде дорівнювати дельта ф0. Оскільки сила, що діє на тіло з боку потоку, буде спрямована по радіусу напівсфери, нам потрібно буде знайти зовнішню межу потоку по відношенню до центру півсфери, тобто точки О. Позначимо відстань до зовнішнього кордону потоку через, так як воно залежить від кута j, який починається від горизонтальної осі Х. Це відстань може бути отримано з трикутника за допомогою теорему косинусів:
[math]L^2f=L^2+l0^2-2L*l0*cosW[/math] (1)
звідки кут гама можна знайти з теореми синусів:
[math]L/sin(180-f)=Lf/sin(W)[/math] (2)
звідси отримаємо:
[math]sinW=(Lf/L)*sinF[/math](3) і [math]cosW=sqrt(1-Lf^2/L^2*sin^2F[/math] (4)
Підставимо [math]cosW[/math] у вираз (1) і отримаємо:
[math]Lf^2=L^2+lo^2-2Llosqrt*(1-(Lf/L)^2sin^2F[/math](5)
для знаходження величини [math]Lf[/math] вираз (5) набуває виду:
[math]L^2+lo^2-Lf^2/2Llo[/math](6)
підносимо до квадрату
[math](L^2+lo^2-Lf^2)^2=4L^2lo^2(1-Lf^2/L^2sin^2F)[/math](7)
Розвязуючи рівняння відносно [math]Lf[/math] отримаємо:
[math]Lf=sqrt(L^2+lo^2-2lo^2sin^2F)[1-sqrt(1-(L^2-lo^2)^2)/(L^2+lo^2-2lo^2sin^2F)][/math] (8)
Подальші розрахунки та детальніше про це
Посилання
--Олександр 16:34, 26 березня 2012 (UTC)