Формули MS Word MathType
Інструкції з написання формул вручну ви можете знайти тут.
Для генерації формул в середовищі MS Word (MathType), необхідно:
Що треба
- MS Word
- MathType вер. 6.Х (www.dessci.com/en/products/mathtype/) - він замінить і значно розширить функціонал стандартного редактора формул, вам сподобається.
Вона платна, рекомендую останню версію 6.7 (див.файлообмінник або шукайте на torrents.ru).
Як вставляти згенеровану формулу з MathType в WiKi
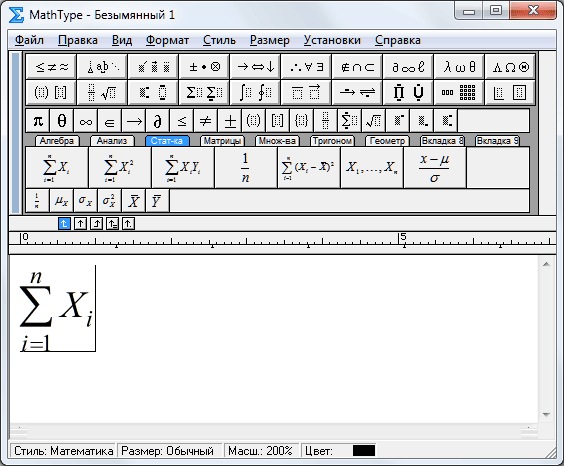
Середовище MathType загалом нагадує інтегрований в MS Word за замовчуванням пакет Microsoft Equation 3.0, але в ньому більше можливостей зокрема щодо вставлення формул практично у будь-які програми, форми й ресурси (розглядається версія 6.7), в т.ч. й у Вікі. Загальний вигляд програми такий:
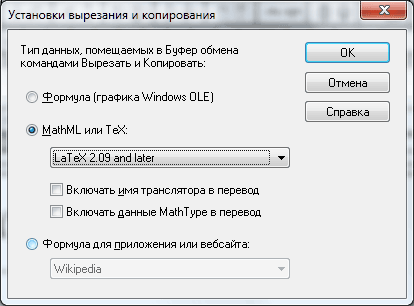
Вставити формулу в ресурс досить просто. Для цього після введення формули в середовищі MathType потрібно в налаштуваннях вказати тип даних, що поміщатимуться у буфер обміну Windows, або власне ресурс, куди надалі пройде вставлення скопійованої в буфер обміну формули. Отже, в російській версії програми (прохання: доповніть мене хтось англійською) виконуємо наступну команду: Установки->Вырезание_и_копирование... З'явиться наступне вікно:
Далі можна піти такими шляхами:
- встановити перемикач налаштувань у варіант MathWL_или_TeX і з випадного списку обрати варіант LaTeX_2.09_and_later;
- або ж у позиції перемикача Формула_для_приложения_или_веб-сайта з випадного списку обрати Wikipedia.
Далі, клацнувши на кнопці ОК, можна "мишковим" (ЛКМ->Копіювати) чи клавіатурним (Ctrl+C) методом скопіювати виділену у середовищі MathType формулу, після чого без трудноців вставити у нашу улюблену Вікіпедію. :-)
Приклади
[math]\sqrt{{{b}^{2}}-4ac}\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\frac{n!}{r!\left( n-r \right)!}[/math]
[math]\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\frac{n!}{r!\left( n-r \right)!}\iint_{\underset{x\to \infty }{\mathop{\lim }}\,}{\sqrt{{{a}^{2}}+{{b}^{2}}}}[/math]
[math]\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}[/math]
[math]\sqrt {{b^2} - 4ac} {{ - b \pm \sqrt {{b^2} - 4ac} } \over {2a}}{{n!} \over {r!\left( {n - r} \right)!}}\mathop {\lim }\limits_{x \to \infty } \int\!\!\!\int_{{{ - b \pm \sqrt {{b^2} - 4ac} } \over {2a}}} {\sqrt {{a^2} + {b^2}} }[/math]
[math]\sqrt{{{b}^{2}}-4ac}\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\frac{n!}{r!\left( n-r \right)!}\underset{x\to \infty }{\mathop{\lim }}\,\iint_{\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}}{\sqrt{{{a}^{2}}+{{b}^{2}}}}[/math]
[math]\sqrt{{{b}^{2}}-4ac}\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\frac{n!}{r!\left( n-r \right)!}\int_{\sqrt{{{a}^{2}}+{{b}^{2}}}}^{{}}{\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}}[/math]
[math]x^3+(sqrt(1/(1+x^(x^3-3))))/(1+x^5-3*4^3+13)[/math]
[math]\operatorname{erfc}(x) = \frac{2}{\sqrt{\pi}} \int_x^{\infty} e^{-t^2}\,dt = \frac{e^{-x^2}}{x\sqrt{\pi}}\sum_{n=0}^\infty (-1)^n \frac{(2n)!}{n!(2x)^{2n}}[/math]
[math]\sum\nolimits_{1}^{1sdfsd}{sdfg}\frac{-b\pm \sqrt{{{b}^{2}}-4asdfsdf\frac{1}{2}\sqrt{sdf\prod\limits_{234}^{sdf}{sdf}}c}}{2a}[/math]
[math]\frac{n!}{r!\left( n-r \right)!}\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\sqrt{{{b}^{2}}-4ac}\underset{x\to \infty }{\mathop{\lim }}\,\infty \bigcap\limits_{{}}{\Epsilon \sum\nolimits_{\frac{n!}{r!\left( n-r \right)!}}^{{}}{\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}}}[/math]