Дискретні розподіли
| {{{img}}} | ||
| Імя | Тарас | |
| Прізвище | Івасюк | |
| По-батькові | Анатолійович | |
| Факультет | ФІС | |
| Група | СН-51 | |
| Залікова книжка | СН-10-055 | |
Зміст
Вступ
Нормальний закон розподілу стосується неперервних випадкових величин. Для дискретних величин він може застосовуватися лише за певних умов, зокрема при великому числі випробувань. Разом з тим число дискретних величин часто не може бути великим (обсяг вибірки невеликий), а крім того, на імовірність тієї чи іншої події (наслідку) впливають деякі обмеження.
Біномінальний розподіл
У робочих процесах АПК, особливо біологічних, найчастіше користуються біноміальним розподілом дискретних величин. Він виникає тоді, коли при будь-якому випробуванні у серії має відбутися одна подія або у деякому розумінні їй протилежна. Вивчення цього розподілу розпочалося з відомої гри в підкидування монет, тому появу однієї події часто називають сприятливим наслідком або успіхом (наприклад, гербом зверху на монеті, що впала, для гравця, який поставив на герб), а протилежної — несприятливим наслідком або невдачею. Ці терміни зберігають свій прямий смисл, наприклад при випробуванні нового препарату на тваринах з можливими наслідками виживає—не виживає.
В основі біноміального закону розподілу лежить загальна схема, названа ім'ям відомого швейцарського вченого математика Якоба Бернуллі. Нехай випадкова величина х набуває тільки двох значень: 1 та 0, причому результати кожного випробування не залежать одні від одних. Ця вимога задовольняється при підкиданні правильної монети. Така схема випробувань лежить в основі широкого кола експериментів, наслідки яких належать двом взаємовиключаючим класам, а розподіл змінної х, яка може набувати тільки двох значень (х = 1 з імовірністю р або х = 0 з імовірністю q = 1 – р), називається розподілом Бернуллі.
Якщо нас цікавить, яка імовірність сприятливого наслідку в серії з N дослідів, то треба врахувати, що число цих наслідків k може набувати будь-яких цілих значень від 0 до N, а число протилежних наслідків дорівнює N – k. При цьому імовірність р (N, k) обчислюється за біноміальним законом
де [math]C_N^k=\frac{N!}{k!(N-k)!}[/math] - біноміальний коефіцієнт.
Параметри N та р повністю визначають біноміальний розподіл.
На рисунку 1 зображено полігони p(N,k) для N=20 та п'яти значень p.
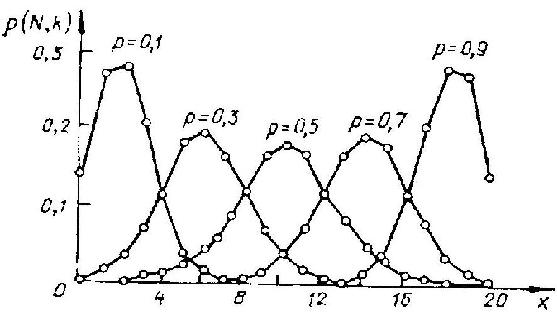
Звідси випливає, що біноміальний розподіл є симетричним тілбки при p=q=0,5. При цьому рівноймовірність наслідківє найчастішою в робочих процесах. При обчисленні теоретичного біноміального розподілу з відомими N та р використовують ту обставину, що р(N, k) є членами в розкладанні бінома Ньютона:
Біноміальні коефіцієнти Сn визначають за допомогою трикутника Паскаля, в якому вони займають рядок з номером N, наприклад для N в межах першого десятка:

Для обчислення р(N, k), починаючи з р(N, 0), можна користуватися також рекурентною формулою:
Дискретний рівномірний розподіл
Нехай маємо урну, в якій є n однакових кульок, пронумерованих числами 1,2,...,n. Яка ймовірність вийняти з урни кульку з номером m? Очевидно, що шукана ймовірність
Розподіл (1.1) називається дискретним рівномірним розподілом. Нижче на рисунку цей розподіл зображено графічно (n=10).
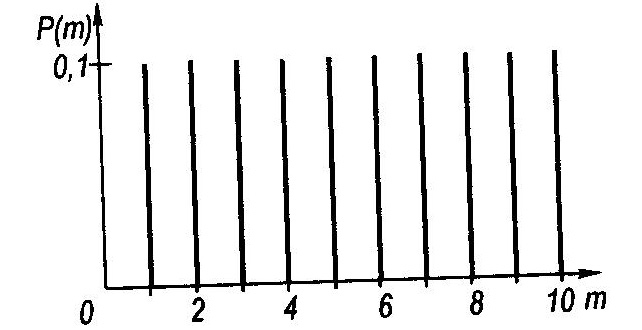
Для випвдкової величини x з дискретним рівномірним розподілом
Приклад
Частота захворювань певною хворобою серед великої рогатої худоби становить 25%. Як оцінити ефективність нової вакцини, якщо щеплення зроблено N здоровим тваринам? Розв'язання З викладеного вище ясно, що оцінка залежить від N. Якщо вакцина не діє, то імовірність того, що всі N тварин залишаться здоровими, становить при N=10 і р=0,75 р(10;10)=0,056, а при N=12 р(12;12)=0,032. Таким чином, відсутність захворювань після щеплення не є повним підтвердженням ефективності вакцини. Імовірність того, що при N=17 матимемо k=16, тобто захворіє одна тварина, р(17;16)=0,050, а при N=23 і k=21 р(23;21)=0,049. Ось чому два захворювання серед 23 тварин краще свідчать на користь вакцини, ніж одне серед 17 тварин або відсутність захворювань серед 10.
Список використаних джерел
1. Математичне планування експериментів в АПК / В. О. Аністратенко, В. Г. Федоров.-К.:Вища школа,1993.-374с.
2. Теорія ймовірностей, випадкові процеси та математична статистика / В. П. Бабак, Б. Г. Марченко, М. Є. Фриз.-К.:Техніка,2004.-285с.