Методи прогнозування

Дана стаття являється неперевіреним навчальним завданням. Студент: hotcoffe Викладач: Назаревич О.Б. Термін до: 28 лютого 2010 До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону.

 http://elartu.tstu.edu.ua/handle/ Презентація доповіді (університетський репозиторій).

Методи прогнозування

До недавнього часу (середини 80-х років минулого століття) існувало декілька загальновизнаних методів прогнозування тимчасових рядів:

• Економетричні • Регресійні • Методи Бокса-дженкінса (ARIMA, ARMA)

Проте, починаючи з кінця 80-х років, в науковій літературі були опубліковані ряд статей з нейромережевої тематики, в яких був приведений ефективний алгоритм навчання нейронних мереж і доведена можливість їх використання для найширшого кола завдань.

Ці статті відродили інтерес до нейромереж в науковому співтоваристві і останні дуже скоро почали широко використовуватися при дослідженнях в самих різних областях науки від експериментальної фізики і хімії до економіки.

Методи прогнозування, засновані на згладжуванні, експоненційному згладжуванні і ковзному середньому

"Наївні" моделі прогнозування

При створенні "наївних" моделей передбачається, що деякий основний період прогнозованого тимчасового ряду краще всього описує майбутнє цього прогнозованого ряду, тому в цих моделях прогноз, як правило, є дуже простою функцією від значень прогнозованої змінної в недалекому минулому.

Найпростішою моделлю є

[math]Y_{t+1}=Y_{t}[/math]

що відповідає припущенню, що "завтра буде як сьогодні"[4].

Поза всяким сумнівом, від такої примітивної моделі не варто чекати великої точності. Вона не тільки не враховує механізми, що визначають прогнозовані дані (цей серйозний недолік взагалі притаменний багатьом статистичним методам прогнозування), але і не захищена від випадкових коливань, вона не враховує сезонні коливання і тенденції. Втім, можна будувати "наївні" моделі дещо по-іншому

[math]\begin{align} & Y_{t+1}=Y_{t}+\left[ Y_{t}-Y_{t-1} \right], \\ & Y_{t+1}=Y_{t}\cdot \left[ Y_{t}/Y_{t-1} \right], \\ \end{align}[/math]

такими способами ми намагаємося пристосувати модель до можливих тенденцій

[math]Y_{t+1}=Y_{t-S}[/math]

це спроба врахувати сезонні коливання.

Середні і ковзаючі середні

Найпростішою моделлю, заснованою на простому усереднюванні [4] є

[math]Y_{t+1}=\frac{1}{t}\left[ Y_{t}+Y_{t-1}+...+Y_{1} \right][/math]

і у відмінності від найпростішої "наївної" моделі, якій відповідав принцип "завтра буде як сьогодні", цій моделі відповідає принцип "завтра буде як було в середньому за останній час". Така модель, звичайно стійкіша до коливань, оскільки в ній згладжуються випадкові викиди щодо середнього. Не дивлячись на це, цей метод ідеологічно настільки ж примітивний як і "наївні" моделі і йому властиві майже ті ж самі недоліки.

У приведеній вище формулі передбачалося, що ряд усереднюється по достатньо тривалому інтервалу часу. Проте як правило, значення тимчасового ряду з недалекого минулого краще описують прогноз, ніж усі попередні значення цього ж ряду. Тоді можна використовувати для прогнозування ковзне середнє

[math]Y_{t+1}=\frac{1}{T+1}\left[ Y_{t}+Y_{t-1}+...+Y_{t-T} \right][/math]

Сенс його полягає в тому, що модель бачить тільки найближче минуле (на T відліків за часом в глибину) і грунтуючись тільки на цих даних будує прогноз.

При прогнозуванні досить часто використовується метод експоненціальних середніх, який постійно адаптується до даних за рахунок нових значень. Формула, що описує цю модель записується як

[math]Y_{t+1}=\alpha Y_{t}+\left( 1-a \right)\hat{Y}_{t},[/math]

де [math]Y_{t+1}[/math] – прогноз на наступний період часу [math]Y_{t}[/math] – реальне значення у момент часу t [math]\hat{Y}[/math] – минулий прогноз на момент часу t а – постійна згладжування (0<=a<=1)

У цьому методі є внутрішній параметр а, який визначає залежність прогнозу від усіх розглянутих даних, причому вплив даних на прогноз експоненціально зменшується із "віком" даних. Залежність впливу даних на прогноз при різних коефіцієнтах а приведена на графіці.

Рис.1 - Режими підйому температури в реакторі

Видно, що при a→1, експоненціальна модель прагне до найпростішої "наївної" моделі. При a→0, прогнозована величина стає рівною попередньому прогнозу.

Якщо проводиться прогнозування з використанням моделі експоненціального згладжування, зазвичай на деякому тестовому наборі будуються прогнози при a=[0.01, 0.02 ..., 0.98, 0.99] і відстежується, при якому а точність прогнозування вища. Це значення а потім використовується при прогнозуванні надалі.

Хоча описані вище моделі ("наївні" алгоритми, методи, засновані на середніх, ковзних середніх і експоненціальному згладжуванні) використовуються при бізнес-прогнозуванні в не дуже складних ситуаціях, наприклад, при прогнозуванні продажу на спокійних і сталих західних ринках, не рекомендовано використовувати ці методи в завданнях прогнозування з причини явної примітивності і неадекватності моделей.

Разом з цим хотілося б відзначити, що описані алгоритми цілком успішно можна використовувати як супутні і допоміжні для передобробки даних в завданнях прогнозування. Наприклад, для прогнозування продажу в більшості випадків необхідно проводити декомпозицію тимчасових рядів (тобто виділяти окремо тенденційну, сезонну і нерегулярну складові). Одним з методів виділення тенденційних складових є використання експоненціального згладжування.

Вимоги до факторів

Фактори повинні бути керованими, це означає, що вибране потрібне значення фактора можна підтримувати постійним протягом всього досліду. Планувати експеримент можна тільки в тому випадку, якщо рівні факторів підкоряються волі експериментатора.

Наприклад, вирощування сільськогосподарських культур залежить від ряду факторів.

Назва фактору	Вид фактору	Характеристика
Щільність посіву	Контр. кількісний	Від щільності посіву залежить врожайність, щільність має свої оптимальні значення. Так коли щільність буде за малою, то більша кількість опадів, буде просто випаровуватись, від чого страждатимуть рослини. При надто щільному посіві рослини не отримуватимуть потрібну кількість сонячних променів.
Використання мінеральних добрив	Контр. кількісний	При використанні мінеральних добрив, слід враховувати їх характеристики, при надмірному використанні добрив, вони спалюють кореневу систему рослин, що зменшує врожайність.
Обробіток	Контр. кількісний	Фактор який впливає на врожайність, коли він буде недостатнім, то корисну культуру витіснять інші не корисні рослини. Це мабуть єдиний фактор який не має верхньої межі.
Вид культури	Контр. якісний	Звісно людина сама вибирає яку культуру їй садити, таким чином усі фактори для отримання найкращого результату врожайності для різних культур матимуть різні значення.
Дата посіву	Контр. якісний	Певні культури необхідно садити в певні часові проміжки часу задля отримання максимальної врожайності (озима пшениця)
Кількість опадів	Не контр. кількісний	На ці фактори людина ніяк не може вплинути, тому його не можна враховувати в експериментах.
Кількість сонячних днів	Не контр. кількісний	На ці фактори людина ніяк не може вплинути, тому його не можна враховувати в експериментах.

Щоб точно визначити фактор, потрібно вказати послідовність дій (операцій), за допомогою яких встановлюються його конкретні значення. Таке визначення називається операційним. Так, якщо фактором є тиск в деякому апараті, то абсолютно необхідно вказати, в якій точці і за допомогою якого приладу він вимірюється і як він встановлюється. Введення операційного визначення забезпечує однозначне розуміння фактору.

Точність вимірів факторів повинна бути максимально високою. Ступінь точності визначається діапазоном зміни факторів. У тривалих процесах, вимірюваних багатьма годинами, хвилини можна не враховувати, а в швидких процесах доводиться враховувати долі секунди.

Дослідження суттєво ускладнюється, якщо фактор вимірюється з великою помилкою або значення факторів важко підтримувати на вибраному рівні (рівень фактора «пливе»), то доводиться застосовувати спеціальні методи дослідження, наприклад, конфлюентний аналіз [1, 2].

Фактори повинні бути однозначні. Важко управляти фактором, який є функцією інших факторів. Але в плануванні можуть брати участь інші фактори, такі, як співвідношення між компонентами, їх логарифми і тому подібне.

Необхідність введення складних факторів виникає за бажання представити динамічні особливості об'єкту в статичній формі.

Наприклад, потрібно знайти оптимальний режим підйому температури в реакторі. Якщо щодо температури відомо, що вона повинна наростати лінійно, то як Фактор замість функції (в даному випадку лінійної) можна використовувати тангенс кута нахилу, тобто градієнт.

Рис.1 - Режими підйому температури в реакторі

При плануванні експерименту одночасно оцінюють декілька факторів, тому необхідно знати вимоги до сукупності факторів. Перш за все висувається вимога сумісності. Сумісність факторів означає, що всі їх комбінації здійсненні і безпечні.

Рис.2 - Схематичне зображення cумісності факторних просторів

Несумісність факторів спостерігається на межах областей їх визначення. Позбавитися від неї можна скороченням областей. Ситуація ускладнюється, якщо несумісність виявляється усередині областей визначення. Одне з можливих рішень - розбиття на підобласті і вирішення двох окремих завдань.

При плануванні експерименту важлива незалежність факторів, тобто можливість встановлення фактора на будь-якому рівні незалежно від рівнів інших факторів. Якщо ця умова нездійсненна, то неможливо планувати експеримент.

Вибір рівнів варіювання факторів і основного рівня

Фактор вважається заданим, якщо вказані його назва і область визначення. У вибраній області визначення він може мати декілька значень, які відповідають числу його різних станів. Вибрані для експерименту кількісні або якісні стани фактору носять назву рівнів фактору.

У плануванні експерименту значення факторів, відповідні певним рівням їх варіювання, виражають в кодованих величинах. Під інтервалом варіювання фактору мається на увазі різниця між двома його значеннями, прийнята за одиницю при кодуванні. [5]

Фактори, що визначають оптимальні будинки для продажу:

Фактор	Вид фактору	К-сть рівнів	Характеристика
Наявність телефону	Якісний	2	Телефон в квартирі або є або його немає.
Ремонт	Якісний	3	Ремонт можна оцінити як відмінний, задовільний та незадовільний.
Відстань до центру міста	Кількісний	100	Визначає відстань від даного будинку до центру міста із кроком 100 м. максимальна відстань до центру міста 10 км.
Кількість кімнат	Кількісний	5	1-кімн. 2-кімн. 3-кімн. 4-кімн. Більше 4 кімн.
Площа 1 кімн….	Кількісний	Х	Відповідно визначається кількість рівнів і крок, верифікації.

При виборі області визначення факторів особливу увагу приділяють на вибір нульової точки, або нульового (основного) рівня. Вибір нульової точки еквівалентний визначенню початкового стану об'єкту дослідження. Оптимізація пов'язана з поліпшенням стану об'єкту в порівнянні з станом в нульовій точці. Тому бажано, щоб дана точка була в області оптимуму або якомога ближче до нього, тоді прискорюється пошук оптимальних рішень. [3]

У випадку лабораторної роботи №1 де фактором виступає кількість присідань і задається значеннями від 0 до 30 із кроком в 10 присідань, маємо: кількість рівнів 4 за нульовий рівень приймаємо рівень 3 – 20 присідань.

Якщо проведенню експерименту передували інші дослідження з даного питання, то за нульову береться така точка, якій відповідає найкраще значення параметра оптимізації, встановленого в результаті формалізації апріорної інформації. В цьому випадку нульовими рівнями факторів є значення останніх спостережень, поєднання яких відповідають координатам нульової точки.

Часто при постановці завдання область визначення факторів буває заданою, будучи локалізованою областю факторного простору. Тоді центр цієї області береться за нульову точку.

Припустимо, в деякому завданні фактор (температура) міг змінюватися від 140 до 180˚С. Природно, за нульовий рівень було прийнято середнє значення фактора, відповідно рівне 160˚С.

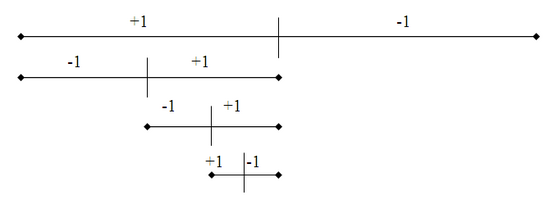
Після встановлення нульової точки вибирають інтервали варіювання факторів. Це пов'язано з визначенням таких значень факторів, які в кодованих величинах відповідають +1 і -1. Інтервали варіювання вибирають з урахуванням того, що значення факторів, відповідні рівням +1 і -1, повинні бути достатньо відмінні від значення, відповідному нульовому рівню. Тому у всіх випадках величина інтервалу варіювання повинна бути більше подвоєної квадратичної помилки фіксації даного фактору.

[math]I=2\cdot(\sum^{n}_{i=1} {p_i})^2[/math]

де p_i – величина закладеної i-ї похибки.

З іншого боку, надмірне збільшення величини інтервалів варіювання небажано, оскільки це може привести до зниження ефективності пошуку оптимуму. А дуже малий інтервал варіювання зменшує область експерименту, що уповільнює пошук оптимуму.

При виборі інтервалу варіювання доцільно враховувати, якщо це можливо, число рівнів варіювання факторів в області експерименту. Від числа рівнів залежать об'єм експерименту і ефективність оптимізації.

У загальному вигляді залежність числа дослідів від числа рівнів факторів має вигляд:

[math]N=P^K[/math],

де:

• N - число дослідів;
• р - число рівнів;
• K - число факторів. [4]

Мінімальне число рівнів, що зазвичай використовують на першій стадії роботи, рівне 2. Це верхній і нижній рівні, що позначаються в кодованих координатах через +1 і -1. Варіювання факторів на двох рівнях використовується у відсіваючих експериментах, на стадії руху в область оптимуму і при описі об'єкту дослідження лінійними моделями. Але таке число рівнів недостатньо для побудови моделей другого порядку (адже фактор приймає тільки два значення, а через дві точки можна провести безліч ліній різної кривизни).

Рис.3 - Схематичне зображення пошуку оптимуму, методом відсіювання.

Із збільшенням числа рівнів підвищується чутливість експерименту, але одночасно зростає число дослідів. При побудові моделей другого порядку необхідні 3, 4 або 5 рівнів, причому тут наявність непарних рівнів указує на проведення дослідів в нульових (основних) рівнях.

У кожному окремому випадку число рівнів вибирають з урахуванням умов завдання і передбачуваних методів планування експерименту.

Рис.4 - Схематичне зображення пошуку оптимуму, інших порядків.

Тут необхідно враховувати наявність якісних і дискретних факторів. У експериментах, пов'язаних з побудовою лінійних моделей, наявність цих факторів, як правило, не викликають додаткових труднощів. При плануванні другого порядку якісні Фактори не застосовні, оскільки вони не мають ясного фізичного сенсу для нульового рівня. Для дискретних факторів часто застосовують перетворення вимірювальних шкал, щоб забезпечити фіксацію значень факторів на всіх рівнях.

Список використаних джерел

1. Клепиков Н.П., Соколов С.Н. Анализ и планирование экспериментов методом максимума подобия. М.: Наука, 1964.
2. Федоров В.В. Теория оптимального эксперимента. М.: Наука, 1971.
3. http://window.edu.ru/window_catalog/pdf2txt?p_id=1180&p_page=1 – Основи планування експериментів (Січень 2010);
4. http://uk.wikipedia.org/wiki/Планування_експерименту – Планування експерименту (Січень 2010);
5. http://www.refine.org.ua/pageid-4881-4.html – Методи досліджень (Січень 2010).

Студент: Користувач:Hotcoffe

Виступ відбувся: 27 січня 2010

Тема: Рівні факторів. Нульовий рівень. Інтервал варіювання фактору.