Капілярний тиск
Капіля́рний тиск (рос. давление капиллярное; англ. capillary pressure, нім. Kapillardruck m) – різниця тисків (±Δp), що виникає внаслідок впливу сил поверхневого натягу на рівновагу або рух вільної поверхні рідини, границі рідини з твердим тілом, а також границі поділу між незмішуваними рідинами, окремий випадок поверхневе явище.
Зміст
Історичні дані
Першовідкривачем капілярних явищ вважається Леонардо да Вінчі. Однак перші акуратні спостереження капілярних явищ на трубках і скляних пластинках були виконані Френсисом Хоксбі 1709 року. Як часто буває, термодинамічний опис виявляється більш простим і більш загальним, не будучи обмеженим недоліками конкретних моделей.
Саме в такий спосіб описав капілярність Гіббс у 1878 р., побудувавши суто термодинамічну теорію. Ця теорія стала невід’ємною частиною гіббсовської термодинаміки. Теорія капілярності Гіббса, не спираючись безпосередньо на які-небудь механістичні моделі, позбавлена недоліків теорії Лапласа; вона може по праву вважатися першою детально розвиненою термодинамічною теорією поверхневих явищ.
Про теорію капілярності Гіббса можна сказати, що вона дуже проста і дуже складна. Проста тому, що Гіббсу удалося знайти метод, що дозволяє одержати найбільш компактні і витончені термодинамічні співвідношення, однаковою мірою застосовні до плоских і скривлених поверхонь.
Капілярні явища в природі і техніці
Завдяки цим явищам відбувається проникнення вологи з ґрунту в стебла і листя рослин. Саме в капілярах відбуваються основні процеси, пов’язані з диханням і живленням організмів. У тілі дорослої людини приблизно 160·109 капілярів, загальна довжина яких сягає 60-80 тис. км.
У будівництві враховують можливість підняття вологи по капілярних порах будівельних матеріалів. Для захисту фундаменту і стін від дії ґрунтових вод та вологи застосовують гідроізоляційні матеріали: толь, смоли тощо.
Часто капілярні явища використовують і в побуті. Застосування рушників, серветок, гігроскопічної вати, марлі, промокального паперу можливе завдяки наявності в них капілярів.
Капілярні явища використовуються під час видобування нафти. Сили взаємодії води з гірською породою більші, ніж у нафти. Тому вода здатна витиснути нафту з дрібних тріщин у більш великі. Для збільшення нафтовіддачі шарів використовуються спеціальні поверхнево-активні речовини.
Як видно з наведеного історичного огляду, капілярні явища вивчаються вже протягом майже трьохсот років. За цей час досить помітно змінилися способи опису капілярних і поверхневих сил. Однак цікаво відзначити, що, починаючи з найперших робіт з теорії капілярних явищ, люди цілком правильно відносили їх до макроскопічних проявів сил, що діють між частинками в речовині. З розвитком уявлень про ці сили мінялося і розуміння їхньої ролі в тих чи капілярних явищах.
Теорія Гіббса
Теорія Гіббса дала цілком новий інструмент дослідження поверхневих явищ. З використанням потужного й універсального апарату термодинаміки удалося дати більш строгі визначення поняттям границі розподілу фаз, товщини плівки і т. ін. Крім того, формула Лапласа для різниці тисків у фазах поблизу скривленої поверхні була отримана в теорії Гіббса без усіляких додаткових припущень про радіус дії міжмолекулярних сил. Підхід, розвинений Гіббсом, і сьогодні не утрачає своєї актуальності в силу своєї універсальності і дивної широти охоплення явищ.
Формула Лапласа
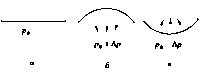
Формула Лапласа. Прагнення поверхні рідини до скорочення приводить до того, що тиск під викривленою поверхнею рідини виявляється іншим, ніж під плоскою поверхнею. Під опуклою поверхнею тиск більше, а під увігнутою менше, ніж під плоскою (рис. 1.1). У випадку увігнутої поверхні поверхневий шар, прагнучи скоротитися, розтягує рідину.Додатковий тиск, обумовлений викривленням поверхні, повинен бути пропорційним поверхневому натягу [math]\sigma [/math] й кривизні поверхні. Обчислимо додатковий тиск для сферичної поверхні рідини. Розсічемо уявно сферичну краплю рідини радіуса R площиною на дві півкулі (рис1.2). Через поверхневий натяг поверхневі шари півкуль притягуються один до одного із силою:
[math]F = 2\pi R\sigma [/math]
де [math]2\pi R[/math] - довжина границі поверхневих шарів півкуль. Ця сила притискає півкулі одна до одної по поверхні площею [math]S = 2\pi {R^2}[/math] й, отже, зумовлює додатковий тиск:
[math]\Delta p = \frac{F}{S} = \frac{{2\pi R\sigma }}{{\pi {R^2}}} = \frac{{2\sigma }}{R}[/math]
Кривизна сферичної поверхні всюди однакова й береться такою, що дорівнює [math]1/R[/math] .
Для характеристики довільної поверхні вводиться поняття середньої кривизни, яке визначається через кривизну нормальних перетинів. Нормальним перетином поверхні в деякій точці називається лінія перетину цієї поверхні із площиною, що проходить через нормаль до поверхні в розглянутій точці. Для сфери будь-який нормальний перетин є коло. У загальному випадку різні нормальні перетини, що проходять через одну і ту саму точку, мають різний радіус кривизни. У геометрії доводиться, що напівсума зворотних радіусів кривизни для будь-якої пари взаємно перпендикулярних нормальних перетинів має одне і теж значення. Ця величина і є середньою кривизною поверхні в даній точці. Легко зрозуміти, що середня кривизна циліндра у два рази менше кривизни сфери того ж радіуса:
[math]H = \frac{1}{2}\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)[/math]
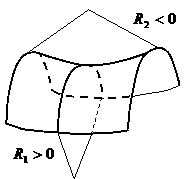
Радіуси [math]{{R_1}}[/math] і [math]{{R_2}}[/math] у формулі є алгебраїчними величинами. Якщо центр кривизни нормального перетину знаходиться під поверхнею, радіус кривизни вважається додатним. Якщо ж центр кривизни нормального перетину знаходиться над поверхнею, радіус кривизни вважається від’ємним (рис. 1.3). Таким чином, неплоска поверхня може мати середню кривизну, яка дорівнює нулю. Для цього потрібно, щоб радіуси кривизни [math]{{R_1}}[/math] і [math]{{R_2}}[/math] були однакові за модулем й протилежні за знаком.
У сфери [math]{R_1} = {R_2} = R[/math],тому [math]H = \frac{1}{R}[/math].
Замінивши у виразі [math]\frac{1}{R}[/math] через [math]H[/math] прийдемо до формули:
[math]\Delta p = 2H\sigma [/math]
Лаплас довів, що формула справедлива для поверхні будь-якої форми, якщо під [math]H[/math] розуміти середню кривизну поверхні в тій точці, під якою визначається тиск. Таким чином, у загальному випадку:
[math]\Delta p = \sigma \left( {\frac{1}{{R{}_1}} + \frac{1}{{R{}_2}}} \right)[/math]
Ця формула називається формулою Лапласа.
Поверхневий натяг
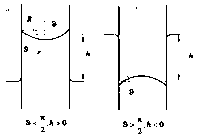
Поверхневий натяг приводить до того, що поблизу стінок посудини поверхня рідини викривляється (дотична до поверхні рідини утворює зі стінкою кут, який дорівнює крайовому куту, що, як правило, відмінний від [math]\frac{\pi }{2}[/math]). У вузькій круглій трубці, яку називають капіляром, або у вузькому зазорі між двома стінками викривленою виявляється уся поверхня (рис. 1.4). Вигнуті поверхні рідини в капілярах називаються менісками. Якщо рідина змочує стінки капіляра, меніск має ввігнуту форму, якщо не змочує – опуклу форму.Коли капіляр занурений одним кінцем у рідину, налиту в широку посудину, тиск під меніском відрізняється від тиску під плоскою поверхнею в широкій посудині на величину [math]\Delta p[/math].
У результаті рівень рідини в капілярі при змочуванні буде вище, ніж у посудині, а при незмочуванні – нижче.
Піднімання або опускання рівня рідини у вузьких трубках одержало назву капілярності. У широкому змісті під капілярними явищами розуміють всі явища, що обумовлені поверхневим натягом. Зокрема тиск називається капілярним тиском.
Між рідиною в капілярі й у широкій посудині встановлюється різниця рівнів [math]h[/math], при якій капілярний тиск [math]\Delta p[/math] урі вноважується гідростатичним тиском [math]\rho gh[/math]
[math]\frac{{2\sigma }}{R} = \rho gh[/math]
де [math]R[/math] радіус кривизни меніска.. З рис. 1.4 бачимо, що радіус кривизни меніска й радіус капіляра пов'язані співвідношенням [math]R = \frac{r}{{\cos \vartheta }}[/math], де [math]\vartheta [/math] - крайовий кут. Підставивши це значення [math]R[/math] і розв’язавши отриману рівність відносно [math]h[/math] прийдемо до формули:
[math]h = \frac{{2\sigma \cos \vartheta }}{{\rho gr}}[/math]
де [math]\sigma [/math] – поверхневий натяг на границі рідина – газ; [math]\vartheta [/math]– крайовий кут; [math]\rho [/math]– густина рідини; [math]g[/math]– прискорення вільного падіння; [math]r[/math] – радіус капіляра. Якщо рідина змочує стінки капіляра, кут [math]\vartheta [/math] гострий, відповідно [math]{\cos \vartheta }[/math] , а отже, і [math]h[/math] додатні (рідина піднімається в капілярі). Якщо рідина не змочує стінки капіляра, то кут [math]\vartheta [/math] тупий, відповідно [math]{\cos \vartheta }[/math] , а виходить, і [math]h[/math] від’ємні (рідина опускається в капілярі).
Література
Фізика - О.В. Лисенко