Критерій Вальда
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
Зміст
Критерії прийняття рішень в умовах повної невизначеності
Критерій прийняття рішень - це функція, що виражає переваги особи, що приймає рішення, і що визначає правило, за яким вибирається прийнятний або оптимальний варіант рішення. Всяке рішень в умовах неповної інформації приймається в з урахуванням кількісних характеристик ситуації, в якій приймаються рішення. Критерії можна використовувати по черзі, причому після обчислення їх значень серед декількох варіантів доводиться довільним чином виділяти деяке остаточне рішення. Що дозволяє, по-перше, краще проникнути в усі внутрішні зв'язки проблеми ухвалення рішень і, по-друге, ослабити вплив суб'єктивного фактору.
Критерій Вальда
Критерій Вальда є критерієм крайнього песимізму, оскільки статистик вважає, що "природа" діє проти нього найгіршим чином. Це критерій гарантованого результату. Нехай гру задано матрицею виграшів гравця А. Тоді на думку статистика - гравця А, дії гравця "природа", якій діє проти нього найгіршим чином, відображуються в реалізації гравцем "природа" таких своїх стані Пj, при яких величина виграшу гравця А (статистика) приймає найменше значення minaij. Виходячи з цього статистик обирає таку чисту стратегію Аi , при якій найменший виграш min aij буде максимальним, тобто забезпечувати максимін:
[math]\alpha_\beta=\max_{i} \min_{j} \alpha_i_j[/math]
Велична аβ , що розраховується за вищенаведеною формулою, називається нижньою ціною гри - це максимальний виграш, що є гарантованим в грі з певним противником шляхом вибору однієї зі своїх стратегій при мінімальних результатах. Нехай гру задано матрицею програшів гравця А, тоді найгірші дії гравця "природа", будуть реалізовуватися в таких станах Пj, при яких величина програшу гравця А (статистика) приймає найбільше значення maxaij. Виходячи з цього статистику необхідно обрати таку чисту стратегію Аi , при якій найбільший програш maxaij буде мінімальним, тобто забезпечувати мінімакс:
[math]\alpha_\beta=\min_{i} \max_{j} \alpha_i_j[/math]
Приклад розвязку
Для гри, яку задано матрицею виграшів, за критерієм Вальда вибрати стратегію, яка є найбільш вигідною.
Розв' язання. Запишемо матрицю виграшів у вигляді таблиці і знайдемо найменше значення minaij для кожного рядка.
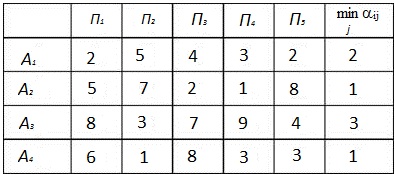
Слід вибрати таку стратегію Аі, і=(1,4), яка є найбільш вигідною(оптимальною), тому маємо [math]\alpha_\beta=\max_{i}(2,1,3,1)=3[/math] що вказує на перевагу стратегії А3
Застосування
Критерій Вальда забезпечує максимізацію мінімального виграшу або, що теж саме, мінімізацію максимального програшу (втрат), який може виникнути при реалізації однієї зі стратегій. Цей критерій орієнтує ОПР дотримуватися вкрай обережної поведінки. Така поведінка прийнятна наприклад, коли гравець не має зацікавленості в крупному виграші, але хоче себе застрахувати від неочікуваних програшів. Вибір такої поведінки визначається відношенням гравця до ризику. Критерій Вальда застосовують у тих випадках, коли необхідно забезпечити успіх в будь-якій ситуації. Застосування критерію Вальда буває виправдано, якщо ситуація, в якій приймається рішення наступна: про можливість появи зовнішніх станів Пj нічого не відомо; доводиться зважати на появу різних зовнішніх станів Пj; рішення реалізується тільки один раз; необхідно виключити який би то не було ризик.
Використана література
1. Математичне планування експериментів в АПК / В. О. Аністратенко, В. Г. Федоров.-К.:Вища школа,1993.-374с.
2. http://pidruchniki.ws/15461213/ekonomika/kriteriyi_priynyattya_rishen_umovah_povnoyi_neviznachenosti
3. http://vtit.kuzstu.ru/books/shelf/book1/doc/gl%2013.html#p13.7.2