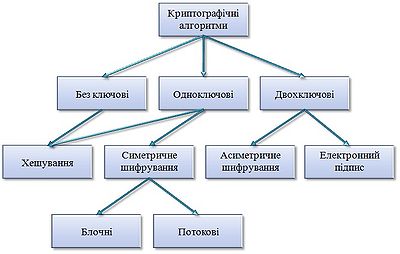
Класифікація криптоалгоритмів
| {{{img}}} | ||
| Імя | Тарас | |
| Прізвище | Куриляк | |
| По-батькові | Тарасович | |
| Факультет | ФІС | |
| Група | СНсп-43 | |
| Залікова книжка | № ПК 08-108 | |
Криптографічний алгоритм, або шифр - це математична формула, що описує процеси шифрування і розшифрування. Щоб зашифрувати відкритий текст, криптоалгоритм працює в сполученні з ключем - словом, числом або фразою.
Криптографічних алгоритмів існує безліч. Їх призначення в загальних рисах зрозуміло: захист інформації. Захищати ж інформацію потрібно від різних загроз і різними способами. Щоб правильно задіяти криптоалгоритм (КА), тобто забезпечити надійний і адекватний захист, потрібно розуміти, які бувають КА і який тип алгоритму краще пристосований для вирішення конкретного завдання.
Зміст
Основна схема класифікації криптоалгоритмів
1. Тайнопис. Відправник і одержувач роблять над повідомленням перетворення, відомі лише їм двом. Стороннім особам невідомий сам алгоритм шифрування. Деякі фахівці вважають, що тайнопис не є криптографією взагалі.
2. Криптографія з ключем. Алгоритм впливу на передані дані відомий усім стороннім особам, але він залежить від деякого параметра - "ключа", яким володіють лише відправник і одержувач.
- Симетричні криптоалгоритми. Для зашифровки і розшифровки повідомлення використовується один і той же блок інформації (ключ).
- Асиметричні криптоалгоритми. Алгоритм такий, що для зашифровки повідомлення використовується один ( "відкритий") ключ, відомий усім бажаючим, а для розшифровки - інший ( "закритий"), який існує тільки в одержувача.
Метод стиснення
Існує багато практичних алгоритмів стиснення даних, але всі вони базуються на трьох теоретичних способах зменшення надлишковості даних. Перший спосіб полягає в зміні вмісту даних, другий - у зміні структури даних, а третій - в одночасній зміні як структури, так і вмісту даних.
Якщо при стисненні даних відбувається зміна їх вмісту, то метод стиснення є незворотнім, тобто при відновленні (розархівуванні) даних з архіву не відбувається повне відновлення інформації. Такі методи часто називаються методами стиснення з регульованими втратами інформації. Зрозуміло, що ці методи можна застосовувати тільки для таких типів даних, для яких втрата частини вмісту не приводить до суттєвого спотворення інформації. До таких типів даних відносяться відео- та аудіодані, а також графічні дані. Методи стиснення з регульованими втратами інформації забезпечують значно більший ступінь стиснення, але їх не можна застосовувати до текстових даних. Прикладами форматів стиснення з втратами інформації можуть бути: JPEG (Joint Photographic Experts Group) для графічних даних:
- MPG - для для відеоданих;
- MP3 - для аудіоданих
Якщо при стисненні даних відбувається тільки зміна структури даних, то метод стиснення є зворотнім. У цьому випадкові з архіву можна відновити інформацію повністю. Зворотні методи стиснення можна застосовувати до будь-яких типів даних, але вони дають менший ступінь стиснення у порівнянні з незворотними методами стиснення. Приклади форматів стиснення без втрати інформації: GIF (Graphics Interchange Format), TIFF (Tagged Image File Format) - для графічних даних; AVI - для відеоданих; ZIP, ARJ, RAR, CAB, LH - для довільних типів даних. Існує багато різних практичних методів стиснення без втрати інформації, які, як правило, мають різну ефективність для різних типів даних та різних обсягів.
Кодування методом Лемпеля-Зіва
Візьмемо набір символів
АБВАБВЯЯЯЯЯЯ
У нім двічі зустрічається поєднання АБВ, тому його можна записати в так званому словнику, а в початковому тексті тільки залишити силку на словник. Тоді початковий текст можна перетворити, наприклад, в
11ЯЯЯЯЯЯ
і окремо запам'ятати, що за символом 1 насправді ховається трійця АБВ . Ясно, що якщо в тексті поєднання АБВ зустрілося не 2 а 100 або ще краще 1000 разів, то стиснення було б вельми відчутним. Проте в реальних ситуаціях на таке везіння розраховувати не слід. Треба все вичавлювати навіть з небагатьох повторень в початковому тексті. Подивимося, чи багато ми вигадали в розглянутому прикладі.
Текст стискувався на 4 символи, але і, як мінімум, 4 символи опинилися у словнику. Крім того, побудова словника зажадає введення роздільників і ін.
Але і це ще не все. А якщо в тексті вже є символи 1 ? Як зрозуміти, що це саме 1, а не посилання на словник? Як же поступити найбільш грамотно? Ось тут відповідь далеко неоднозначна. Вона і не може бути однозначна, тому що стиснення - це не таблиця множення. Один текст краще стискається одним методом інший - абсолютно іншим способом. Спершу ми розглянемо дуже спрощений варіант, щоб від чого відштовхуватиметься надалі.
Для визначеності вважатимемо, що кожен символ в тексті - це впорядкований набір з 8 бітів, тобто байт, або, що те ж саме ціле число від 0 до 255.
Послідовно читаємо початковий текст і одночасно формуємо вихідний файл. Якщо чергова буква зустрілася вперше, або вона виявилася останньою в тексті, то на вихід посилаємо біт 1 і 8 бітів від самої цієї букви. Так само треба поступити, якщо символ не новий але в парі з наступним ще не зустрічався. Отже в нашому прикладі перші три символи дадуть на виході 27 бітів. Тоді при зворотній операції як тільки той, що розшифровує побачив черговий біт 1, він відразу знатиме, наступні за ним 8 бітів треба вивести, так би мовити відкритим текстом.
Якщо черговий символ в парі з наступним за ним вже зустрічався то в принципі від цієї пари можна вивести два біта 01 і вказівку на існуючу аналогічну пару. Тоді декодувальник, побачивши 01, по цій вказівці подивиться на вже розшифровану частину тексту, візьме потрібну пару і припише таку саму в кінець розшифрованої частини.
В нашому прикладі достатньо двох байт них посилань. Отже на вихід пошлемо:
Далі від букви Я по відомих правилах піде 9 бітів. Залишок тексту шифрується сімома бітами:
Перша група з нулів, що закінчується одиницею, означає, що раніше в тексті вже була аналогічна п'ятірка символів. Друга група представляє число одиницю, вказуюче, на якій відстані треба шукати прототип. Прототип добудовуватиметься по ходу будівництва копії з нього, але випереджаючими темпами, достатніми для того, щоб копіювання не простоювало.
Таким чином, початковий текст в стислому вигляді при декілька вільному зображенні з'явиться у вигляді:
Правильніше (але менш наочно) було б вписати замість А, Би і В їх восьмибітові уявлення
.
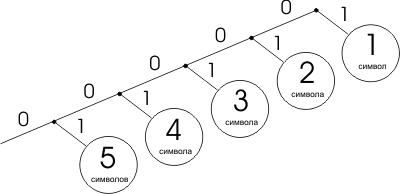
Дерево Лемпеля-Зіва виглядає так:
Щоб програма розшифровки годилася не тільки для розглянутого прикладу, ще до стислого тексту треба прикласти деякі параметри: довжину стислого або розгорненого тексту, а також довжину посилань. Само дерево прикладати не треба, якщо воно підкоряється простим широкоспоживаним правилам.Отже дерево Лемпеля-Зіва може бути достатнє складним і розлогим.
Дешифрування
Далі приводиться алгоритм дезархівації зі всіма необхідними технічними подробицями і ретельно підібраними значеннями параметрів. Річ у тому, що навіть дуже невеликі варіації параметрів різко міняють ступінь стиснення і, як правило, в гіршу сторону. А боротьба ведеться за долі відсотка. Завдання ускладнюється тим, що немає об'єктивних критеріїв, по яких можна було відразу сказати, що та або інша зміна алгоритму пішла йому на користь. Як ми знаємо, для будь-якого архіватора знайдеться сила-силенна текстів, взагалі непіддатливих стисненню.
Якщо брати тільки такі тексти, то роботу можна не починати. Оцінювати архіватор треба по ходових текстах, але ходові - це не наукове поняття .
3Читається чергова серія бітів до першого одиничного біта. Хай N - кількість лічених бітів. Наприклад, якщо на черги 001000..., то прочитуються 3 бфта і відповідно N=3.А якщо перший же біт дорівнює одиниці, то прочитується тільки він, і
N=1. Вводимо число M для формування кількості символів, які пізніше будуть узяті з вже розшифрованого тексту. Спочатку M=N. Числа M і N - цілі двохбайтні.
- Якщо N більше або рівне 17, то прочитуються чергові 8 бітів і поміщаються в молодші біти числа M.
- Якщо N > 17, то прочитуються чергові 8 бітів і поміщаються в старший байт числа M. (Воно вважається за беззнакового.)
- Якщо M=1, то прочитуються чергові 8 бітів і посилаються на вихід, тобто у відновлений текст, і тоді перехід на п.1.
- Прочитуються чергові 2 біта, по яких формується ціле число Z від 0 до 3. Вводимо K і R.Якщо M=2, Z=0, то K=5, R=0. Якщо M=2, Z=1, то K=7, R=-32.
- Прочитуються чергові K бітів і поміщаються в молодші K бітів допоміжного цілого двобайтного числа S. Решта бітів цього числа заповнюються одиницями. Отже S<0, оскільки в старшому біті, що відповідає за знак, знаходиться одиниця.
- Визначається адреса в тексті, що випускається, звідки буде узятий потрібний фрагмент. Адреса - це просто номер байта в послідовності їх розташуванні. Для цього до адреси, на якій поки закінчено формування розшифрованого тексту, треба додати R і S. З отриманої таким чином адреси беремо M символів і додаєм в кінець формованого тексту. Перехід на п.1 (якщо дані не вичерпані). Наступна реалізація алгоритму призначена для COM-програм, що саморозархівовуються. Тому перший десяток команд в основному служить для переміщення програми в кінець сегменту код. А вже звідти розшифровані оператори складуються в початок цього сегменту.
Варіанти удосконалення
Приведені вище деталі алгоритму і значення параметрів не можуть бути виведені якими-небудь раціональними строгими методами. У якійсь мірі в них відбиті особливості сучасного програмування і людської мови. Але автори кожного архіватора знаходять свій оптимум, і що краще - може підказати тільки практика (критерій загальний, але декілька розпливчатий).
Могутні архіватори зазвичай роблять попередню оцінку початкового файлу і до кожного файлу (або до великих частин одного файлу) здійснюють індивідуальний підхід. Наприклад, перед кожним великим фрагментом стислої коди вказується його об'єм і тип стискування для цього досить 3 байти, які не псують загальної якості компресії.
Якщо файл короткий, значить, взагалі дезархіватору не знадобиться заглядати далеко назад, тоді не потрібний, скажімо випадок K=14, і біти, що звільнилися, можна використовувати з більшою користю. Проте ефект порівняно невеликий. А оскільки він виявляється тільки на малих файлах, то на загальних (зазвичай гігантських) об'ємах інформації він і зовсім втрачається.
Можливі багато інших варіантів удосконалень, не пов'язаних безпосередньо з характерними для Лемпеля-зіва ідеями. Важливий випадок, коли чисельна інформація набита цифрами. Наприклад: 132, -44.8, 555. Зрозуміло, що цифри можуть бути так перетасовані, що навіть однакові пари будуть украй рідкісні. Згадані методи не дають стиснення. Проте, якщо у фрагменті тексту використовуються всього 16 різних знаків, то кожен з них представляється чотирма бітами. А це вже двократне стиснення! Додаткові резерви можуть бути розкриті якщо текст - російською мовою і використовується не більше 64 знаків.
Можна виділяти в початковому файлі нестискувані ділянки. Тоді збиток від кожного з них можна понизити до 3 байтів. А в представленому варіанті кожен перенесений без змін символ тягне за собою однобайтну ознаку, тобто збиток 12.5%!
Проте викладений вище алгоритм не враховує такі деталі тому що вони відносно рідкісні, а ефект від них скромний.