Сопла Лаваля
Сопло Лаваля — технічне пристосування, яке служить для прискорення газового потоку, що проходить по ньому до швидкостей, що перевищують швидкість звуку. У найпростішому випадку сопло представляє собою циліндричний або конічний патрубок (насадок), один кінець якого приєднаний до джерела рідини чи газу, а з іншого виходить сформований струмінь.
Принцип дії
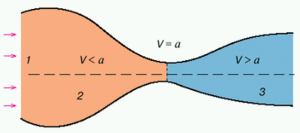
Сопло Лаваля – це комбіноване сопло, яке спочатку звужується, а після розширюється. В самому вузькому місці(найменше січення) завжди встановлюється критична швидкість [math]{\omega _{2kp}}[/math] і максимальна витрата.В розширюючій частині при постійній витраті [math]{m_{\max }}[/math] швидкість зростає, а її величина визначається з рівняння (1):
[math]{\omega _2} = \sqrt {2\frac{k}{{k - 1}}} {P_1}{V_1}\left[ {1 - {{\left( {\frac{{{P_2}}}{{{P_1}}}} \right)}^{\frac{{k - 1}}{k}}}} \right][/math] - швидкість потоку
Сопло використовується для раціонального використання енергії потоку при умові, що
[math]\frac{{{P_2}}}{{{P_1}}} \triangleleft {\beta _{kp}}[/math]. Розміри сопла визначаються з рівняння (2) у випадку коли відома витрата
m. Спочатку знаходимо площу мінімального січення сопла і його діаметр.
Довжина розширюючої частини визначається:
[math]l = \frac{{D - d}}{{2tg\frac{\alpha }{2}}}[/math], де
- D – діаметр вихідного січення;
- d – мінімальний діаметр сопла (у найвужчій частині);
- α - кут конусності, який вибирають з умови неперервності потоку;
- α=10-12°
Феномен прискорення газу до надзвукових швидкостей в соплі Лаваля був виявлений в кінці XIX ст. експериментальним шляхом. Пізніше це явище знайшло теоретичне пояснення в рамках газової динаміки.
При наступному аналізі перебігу газу в соплі Лаваля приймаються наступні допущення:
- Газ вважається ідеальним.
- Газовий потік є ізоентропним (тобто має постійну ентропію, сили тертя і дисипативні втрати не враховуються) і адіабатичним (тобто теплота не підводиться і не відводиться).
- Газова течія є стаціонарним і одновимірним, тобто в будь-якій фіксованій точці сопла всі параметри потоку постійні в часі і змінюються тільки уздовж осі сопла, причому у всіх точках обраного поперечного перерізу параметри потоку однакові, а вектор швидкості газу всюди паралельний осі симетрії сопла.
- Масова витрата газу однакова у всіх поперечних перерізах потоку.
- Вісь симетрії сопла є просторовою координатою.
Ставлення локальної швидкості [math]\,v[/math] до локальної швидкості звуку [math]\, C[/math] позначається числом Маха, яке також розуміється місцевим, тобто залежним від координати [math]\, x[/math]:
З рівняння стану ідеального газу слідує:[math]\frac{dp}{d\rho}=C^2[/math], тут [math]\,\rho[/math] - локальна щільність газу, [math]\, p[/math] - локальне тиск. З урахуванням цього, а також з урахуванням стаціонарності і одномірності потоку рівняння Ейлера набуває вигляду:
що, враховуючи (3), перетворюється в [math]\frac{1}{\rho}\cdot \frac{d\rho}{dx} = -M^2\cdot \frac{1}{v}\cdot \frac{dv}{dx}[/math]. (4)
Рівняння (4) є ключовим у даному міркуванні.
Розглянемо його в такій формі:
Величини [math]\frac{1}{\rho} \frac{d\rho}{dx}[/math] и [math]\frac{1}{v} \frac{dv}{dx}[/math] характеризують відносну ступінь змінності по координаті [math]\,x[/math] щільності газу і його швидкості відповідно. Причому рівняння (4.1) показує, що співвідношення між цими величинами рівне квадрату числа Маха (знак мінус означає протилежну спрямованість змін: при зростанні швидкості щільність убуває). Таким чином, на дозвукових швидкостях [math]\,(M\lt 1)[/math] щільність змінюється в меншій мірі, ніж швидкість, а на надзвукових [math]\,(M\gt 1)[/math] - навпаки. Як буде видно далі, це і визначає звужуючу-розширюючу форму сопла.
Оскільки масова витрата газу постійна:
где [math]\, A[/math] - площа місцевого перетину сопла,
диференціюючи обидві частини цього рівняння по [math]\, x[/math], одержуємо:
Після підстановки з (4) в це рівняння, отримуємо остаточно:
Зауважимо, що при збільшенні швидкості газу в соплі знак вираження [math]\frac{A}{v}\cdot\frac{dv}{dx}[/math] позитивний і, отже, знак похідної [math]\frac{dA}{dx}[/math] визначається знаком вираження : [math]\,({M^2 - 1})[/math]
З чого можна зробити наступні висновки:
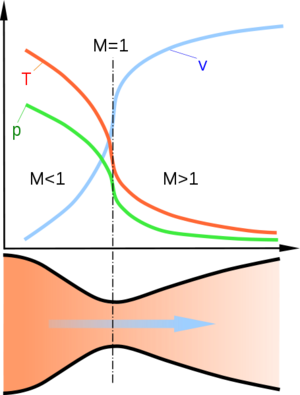
- При дозвуковой швидкості руху газу [math]\,(M\lt 1)[/math], похідна [math]\frac{dA}{dx}\lt 0[/math] - сопло звужується.
- При надзвуковій швидкості руху газу [math]\,(M\gt 1)[/math], похідна [math]\frac{dA}{dx}\gt 0[/math] - сопло розширюється.
- При русі газу зі швидкістю звуку [math]\,(M = 1)[/math], похідна [math]\frac{dA}{dx}=0[/math] - площа поперечного перерізу досягає екстремуму, тобто має місце найвужчий перетин сопла, званий критичним.
Отже, на звуженій, докритичній ділянці сопла рух газу відбувається з дозвуковими швидкостями. У найвужчому, критичному перетині сопла локальна швидкість газу сягає звуковій. На розширеній, закритичній ділянці, газовий потік рухається з надзвуковою швидкістю, прискорюючись. Це прискорення відбувається завдяки тому, що хвиля зниження тиску від розширеної порції газу в надзвуковому потоці не встигає розповсюдитися на наступні за нею інші порції. Закон Бернуллі в цих умовах не виконується. Як наслідок цього, маємо корисну роботу.
Використання сопла Лаваля
Широко використовується в парових і газових турбінах, ракетних і повітряно-реактивних двигунах, газодинамічних лазерах, обладнанні для нанесення фарб, абразиво-струминній обробці тощо.
Залежно від технічного призначення сопла виникають специфічні завдання розрахунку: наприклад, в соплі аеродинамічних труб необхідно забезпечити створення рівномірного і паралельного потоку газу у вихідному перетині, вимоги до сопла ракетних двигунів полягають в здобутті найбільшого імпульсу газового потоку у вихідному перетині сопла при його заданих габаритних розмірах.
Ці та інші технічні завдання привели до бурхливого розвитку теорії сопла, що враховує наявність в газовому потоці рідких і твердих часток, нерівноважних хімічних реакцій, перенесення променистої енергії, що зажадало широкого вживання ЕОМ(електронна обчислювальна машина) для вирішення вказаних завдань, а також для розробки складних експериментальних методів дослідження сопла. nbsp;(4)
Рівняння (4) є ключовим у даному міркуванні. Розглянемо його в такій формі: