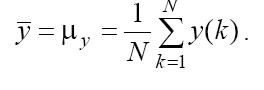Кореляційний аналіз

Дана стаття являється неперевіреним навчальним завданням. Студент: inna Викладач: Назаревич О.Б. Термін до: 9 квітня 2010 До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону.

....... Презентація доповіді (університетський репозиторій).

Кореляційний аналіз, мета і завдання

Кореляційний аналіз – це статистичне дослідження (стохастичної) залежності між випадковими величинами (англ. correlation – взаємозв’язок). У найпростішому випадку досліджують дві вибірки (набори даних), у загальному – багатовимірні комплекси (групи) геологічних параметрів або об’єктів.

Мета кореляційного аналізу – забезпечити отримання деякої інформації про одну змінну за допомогою іншої змінної. В випадках, коли можливе досягнення мети, говорять, що змінні корелюють. В самому загальному вигляді сприйняття гіпотези про наявність кореляції означає, що зміна значення змінної А відбудеться одночасно з пропорційною зміною значення В.

Мірою залежності між експериментальними наборами даних є числа – коефіцієнти зв’язку.

Головні завдання кореляційного аналізу:

1) оцінка за вибірковими даними коефіцієнтів кореляції;

2) перевірка значущості вибіркових коефіцієнтів кореляції або кореляційного відношення;

3) оцінка близькості виявленого зв’язку до лінійного;

4) побудова довірчого інтервалу для коефіцієнтів кореляції.

Визначення сили та напрямку взаємозв’язку між змінними є однією з важливих проблем аналізу даних. В загальному випадку для цього застосовують поняття кореляції.

Поняття кореляції

Коефіцієнт кореляції, а в загальному випадку кореляційна функція, дозволяють встановити степінь взаємозв’язку між змінними. Кореляція може бути лінійною або нелінійною в залежності від типу залежності, яка фактично існує між змінними. Досить часто на практиці розглядають тільки лінійну кореляцію (взаємозв’язок), але більш глибокий аналіз потребує використання для дослідження процесів нелінійних залежностей. Складну нелінійну залежність можна спростити, але знати про її існування необхідно для того, щоб побудувати адекватну модель процесу.

Рис. 1.1 - Ілюстрація «простої» кореляції

Формула для обчислення коефіцієнтів кореляції має вигляд:

де N − довжина вибірки даних; x, y − середні вибіркові x, y ; σx,σ y − стандартні відхилення, тобто корені квадратні з їх дисперсій.

Наприклад,

де N − число вимірів змінної y ; y − середнє значення ряду {y(k)}, яке обчислюється за формулою:

Часткова та напівчасткова кореляції

У випадку двох нормальних або майже нормальних величин коефіцієнт кореляції між ними може бути використаний як міра взаємозв’язку і це підтверджено багатьма практичними результатами. Проте при інтерпретації «взаємозв’язку» часто виникають наступні труднощі: якщо одна величина корельована с іншою, то це може бути відображенням того факту, що вони обидві корельовані з деякою третьою величиною або з сукупністю величин, які залишаються за кадром і не введені в модель. Така ситуація приводить до розгляду умовних кореляцій між двома величинами при фіксованих значеннях інших величин. Це так звані часткові кореляції. Якщо кореляція між двома величинами зменшується, коли ми фіксуємо деяку іншу випадкову величину, то це означає, що їх взаємозв’язок виникає частково через вплив цієї величини. Якщо ж часткова кореляція дорівнює нулю або дуже мала, то робимо висновок, що їх взаємозв’язок цілком обумовлений власним впливом і ніяк не пов’язаний з третьою величиною.

І навпаки, якщо часткова кореляція більше початкової кореляції між двома величинами, то ми робимо висновок, що інші величини ослабили зв’язок, або приховали (замазали) кореляцію.

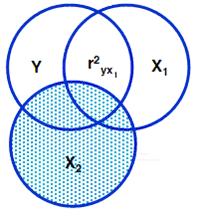
Розрізняють поняття напівчасткової та часткової кореляції. Розглянемо ситуацію для трьох змінних (два при Х1 та Х2 (пояснюючі, незалежні змінні) і одна змінна відклику Y (залежна змінна, змінна критерію)). Часткова та напівчасткова кореляції позбавляють впливу третьої змінної.

Рис. 1.2 - Ілюстрація кореляції трьох змінних

Значення напівчасткової та часткової кореляції можна виразити через множинну кореляцію. Множинна кореляція у випадку трьох змінних обчислюється за формулою:

Напівчасткова кореляція названа так, тому що дисперсія контрольованої змінної (Х2) усувається з іншої незалежної змінної (Х1), але не із залежної змінної (Y). Тобто ми позбавляємось лише впливу Х2 на Х1.

Рис. 1.3 - Ілюстрація напівчасткової кореляції

У випадку трьох змінних формула для обчислення напівчасткової кореляції буде мати вигляд:

В термінах звичайних коефіцієнтів кореляції отримаємо:

де - проста кореляція між у та х1

- результат кореляції між у і х2 та х1 і х2

- загальна дисперсія за винятком взаємозв’язку між х1 і х2

Часткова кореляція відрізняється від напівчасткової тим, що усувається вплив третьої змінної з іншої незалежної змінної, а також і з залежної змінної.

Рис. 1.4 - Ілюстрація часткової кореляції

У випадку трьох змінних формула для обчислення часткової кореляції буде мати вигляд:

В термінах звичайних коефіцієнтів кореляції отримаємо:

- проста кореляція між у та х1

- результат кореляції між у і х2 та х1 і х2

- загальна дисперсія за винятком всіх часткових взаємозв’язків (між х1 і х2 та у і х2)

Якщо кореляція між х1 і х2 та у і х2 відсутня, то

Властивості коефіцієнта кореляції

1. Коефіцієнт кореляції є в межах від -1 до +1.

[math]-1\le \rho (x,y)\le +1[/math]

Якщо [math]\rho (x,y)\gt 0[/math], то кореляція пряма, а якщо [math]\rho (x,y)\lt 0[/math] – зворотна. Пряма кореляція: більшим значенням випадкової змінної [math]x[/math] відповідають більші значення [math]y[/math]; зворотна кореляція: більшим значенням [math]x[/math] відповідають менші [math]y[/math] і навпаки, більшим [math]y[/math] – менші [math]x[/math].

2. Симетрія

[math]\rho (x,y)=\rho (y,x)[/math]

3. Якщо [math]x[/math] та [math]y[/math] пов’язані лінійним функціональним зв’язком [math]y\left( x \right)=a+bx[/math], [math]a[/math] i [math]b[/math] – сталі, то [math]\left| \rho (x,y) \right|=1[/math], і навпаки.

4. Якщо випадкові змінні лінійно незалежні, то [math]\rho (x,y)=0[/math], і навпаки. Останні дві властивості можна сформулювати як необхідну й достатню умови, причому критерієм залежності випадкових величин [math]x[/math] і [math]y[/math] є відмінність коефіцієнта кореляції від нуля: [math]r\ne 0[/math].

Кореляційне поле

Графічно дані для кореляційного аналізу зображають у вигляді кореляційного поля, тобто точок на площині, кожна з яких має координати [math]({{x}_{i}},{{y}_{i}})[/math] (рис.3.1)

Список використаних джерел

1. Курсова робота на тему: “Розробка методів для обчислення часткової кореляційної функції”.
2. http://uk.wikipedia.org/wikiАвтокореляція
3. http://www.lnu.edu.ua/faculty/geology/phis_geo/Khomyak/E-book_Geostatistics/Part2/Lections2-3-1.htm
4. Аністенко В.О., Федоров В.Г. – Математичне планування експерименту АПК.

Студент: Користувач:inna

Виступ відбувся: 9 березня 2010

Тема: Кореляційний аналіз експериментальних даних. Кореляційна матриця. Перевірка гіпотез відносно значень кореляційної матриці