Насадка Вентурі
Зміст
Насадка Вентурі
Насадка зовнішня, Насадка Вентурі (рос. насадка внешняя (Вентури); англ. external mouthpiece (Venturi); нім. Aussenaufsatz m, Ausseneinsatz m, Venturi-Düse f) – циліндрична насадка, розміщена з зовнішнього боку стінки посудини (або водойми), з якої вона живиться. Коефіцієнт витрати зовнішньої насадки більший за коефіцієнт витрати внутрішньої при інших рівних умовах.
Історія розвитку
Джованні Баттіста Вентурі (11 вересня 1746 - 10 вересня 1822) - італійський вчений, відомий роботами в галузі гідравліки, теорії світла і оптики. Його ім'ям названо відкритий ним ефект зниження тиску газу або рідини зі збільшенням швидкості їх руху, а також труба Вентурі.
Народився в Біббіано, сучасник Леонарда Ейлера і Данила Бернуллі, учень Ладзаро Спаланцані.
У 1769 був посвячений у священика і в тому ж році призначений на посаду вчителя логіки в семінарію Реджо-Емілія. У 1774 став професором геометрії та філософії Моденского університету, через два роки - професором фізики.
Вентурі був першим, хто привернув увагу до особистості Леонардо да Вінчі як вченого, і зібрав і опублікував безліч робіт і записів Галілея.
Помер в Реджо-Емілії в 1822.
Теоретичні відомості
Насадки Вентурі, як і діафрагма, представляють деякі гідравлічні опори на шляху руху повітря і тому, щоб мати перед двигуном атмосферний тиск, в багатьох випадках в систему вводять додатково нагнітаючий вентилятор. Рідина, протікаючи через насадку Вентурі, спочату зжимається, а потім розширяється і заповняє всю трубку. Через це коефіцієнт Вентурі майже на 30% перевищує розхід.
Витратоміри перемінного перепаду тиску
Витратоміри перемінного перепаду тиску складаються з трьох елементів: звужуючого пристрію, диференціального манометра і з'єднувальних ліній з запірною і запобіжною арматурами. Застосовуються наступні стандартні звужуючі пристрої: діафрагма, сопла, сопла Вентурі і труби Вентурі. Для виводу основного рівняння розходу рідини, протікающої через звужений пристрій, використовується рівняння Бернуллі. Площина порівнянь проводиться по осі трубопроводу. Втрати напору між січенням не враховується В цьому випадку рівняння Бернуллі матиме вигляд
[math]\frac{{{p_{_1}}}}{{\rho g}} + \frac{{{\alpha _1}{\upsilon _1}^2}}{{2g}} = \frac{{{p_2}}}{{\rho g}} + \frac{{{\alpha _2}{\upsilon _2}^2}}{{2g}}[/math] (3.1)
Приймаючи до уваги a1 = a2 = 1,використовуючи рівняння нерозривності [math]{\upsilon _1}{\omega _1} = {\upsilon _2}{\omega _2}[/math] і враховуючи, що [math]\frac{{{p_1}}}{{\rho g}} - \frac{{{p_2}}}{{\rho g}} = h[/math]вирішується рівняння відносно v1:
[math]{\upsilon _1} = \frac{{\sqrt {2g} }}{{\sqrt {{{\left( {\frac{{{\omega _1}}}{{{\omega _2}}}} \right)}^2} - 1} }}\sqrt h[/math] (3.2)
Теоретична витрата в трубопроводі визначається за формулою
[math]{Q_T} = {\omega _1}{\upsilon _1} = \frac{{{\omega _1}\sqrt {2g} }}{{\sqrt {{{\left( {\frac{{{\omega _1}}}{{{\omega _2}}}} \right)}^2} - 1} }}\sqrt h[/math] (3.3)
Рівняння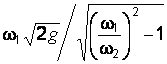 
залежить тільки від геометричних розмірів даного витратоміра і є постійною величиною:
[math]\frac{{{\omega _1}\sqrt {2g} }}{{\sqrt {{{\left( {\frac{{{\omega _1}}}{{{\omega _2}}}} \right)}^2} - 1} }} = C[/math] (3.4)
Тоді рівняння витрати набуде вигляду
[math]{Q_T} = C\sqrt h[/math] (3.5)
де С - постійна витратоміра.
При виведенні залежності (3.5) не враховувалися втрати енергії, тому фактична витрата буде меншою теоретичної. Ця невідповідність видатків характеризується коефіцієнтом витрати
[math]\mu = \frac{Q}{{{Q_T}}}[/math] (3.6)
Остаточна формула для визначення витрати приймає наступний вигляд:
[math]Q = \mu C\sqrt h = A\sqrt h[/math] (3.7)
де А - коефіцієнт витрати витратоміра,
[math]A = \mu C[/math] (3.8)
Витікання рідини через отвори і насадки. Водозливи
Короткий патрубок, приєднаний до отвору в тонкій стінці, а так само коротка труба в товстій стінці, довжина яких не перевищує (3? 7d), називаються насадками.
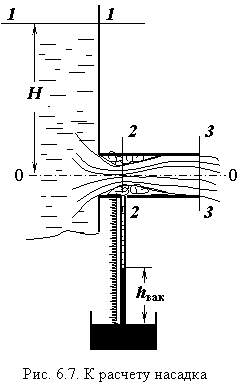
Приєднання насадка до отвору того ж діаметру змінює характер перебігу. Це добре можна показати, застосовуючи рівняння Бернуллі до січень 1-1 і 2-2, а потім 1-1 і 3-3.
Як можна бачити (рис. 6.7), протягом рідини в насадці можна розділити на дві зони. Основна частина - це власне струмінь. Течія в області стиснутого перерізу (2-2), нестала. Воно виникає внаслідок того, що при видаленні повітря з цієї області на початку руху, тут утворюється зона розрідження. Величину вакууму легко вимірюють за допомогою вакуумметра будь-якої конструкції. Наявність вакууму всередині насадка, приєднаного до отвору, сприяє додатковому підсосу рідини і збільшення пропускної здатності отвори, що визначається за рівнянням Бернуллі для перерізів 1-1 і 2-2
[math]{z_1} + \frac{{{p_1}}}{{\rho g}} + \frac{{{\alpha _1}{\upsilon _1}^2}}{{2g}} = {z_2} + \frac{{{p_2}}}{{\rho g}} + \frac{{{\alpha _2}{\upsilon _2}^2}}{{2g}} + {h_{1 - z}}[/math]
Після підстановки значень визначається величина швидкості витікання через отвір при наявності насадка:
[math]{H_1} + \frac{{{p_a}}}{{\rho g}} = \frac{{{p_a}}}{{\rho g}} - \frac{{\rho g{h_{}}}}{{\rho g}} + \frac{{\alpha {\upsilon _c}^2}}{{2g}} + {\xi _{}}\frac{{{\upsilon _c}^2}}{{2g}}[/math]
[math]{H_1} + {h_{}} = \frac{{\alpha {\upsilon ^2}_c}}{{2g}} + {\xi _{}}\frac{{{\upsilon ^2}_}}{{2g}}[/math]
[math]{\upsilon _c} = \phi \sqrt {2g(H + {h_{}})}[/math] Як можна бачити, відбувається збільшення чинного напору на величину вакууму в області стиснутого перерізу. Якщо підставити значення вакууму для розглянутого зовнішнього циліндричного насадка hвак = 0,75 H, то величина швидкості витікання, а, отже, і витрати збільшиться в 1.32 рази, тобто на 32%.
При розгляді перерізів 1-1 і 3-3 будуть отримані формули. Так, на рис. 6.7 видно, що струмінь на виході з насадка займає весь переріз патрубка, тобто стиск на виході відсутній і коефіцієнт стиснення Eн = 1. У тому випадку, якщо струмінь не доходить до стінок патрубка, вакуум в стислому перерізі не утворюється, насадок не працює, витікання відбувається через отвір, і збільшення витрат немає. Для створення умов роботи насадка його довжина повинна бути не менше трьох розмірів отвору.
Отже, розрахункові формули для насадок мають такий вигляд:
Перелік посилань
http://edu.dvgups.ru/METDOC/ITS/GIDRA/GIDRAVL/METOD/AKIMOV/frame/3_1.htm
