Особливості планування експериментів

Дана стаття являється неперевіреним навчальним завданням. Студент: Mars Викладач: Назаревич О.Б. Термін до: 17 лютого 2010 До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону.

Експеримент, в якому реалізуються всі можливі сполучення рівнів факторів, називається повним факторним експериментом.

http://elartu.tstu.edu.ua Презентація доповіді (університетський репозиторій).

Особливості планування експериментів

Опишемо послідовність Дій, які необхідно виконувати під час планування експериментів.

1. Визначення відгуків (вихідних змінних) системи.
2. Визначення факторів, які впливають на відгук системи. Більшість систем підпорядковуються принципу Парето - з огляду на характеристики системи істотними є лише деякі з множини факторів. У більшості систем 20 % факторів визначають 80 % властивостей системи.
3. Визначення рівнів факторів. Мінімальна кількість рівнів для кожного фактора два - нижня і верхня межі значення фактора. У разі використання цього числа рівнів можна визначити тільки лінійні ефекти. Для врахування квадратичних ефектів необхідно використовувати три рівні, для кубічних ефектів - чотири і т. д Аналіз значно спрощується, якщо брати тільки рівновіддалені одне від одного значення рівнів. У цьому випадку маємо так зване ортогональне планування, або ортогональний експеримент.

Для множинних експериментів з чистом факторів більше одного дисперсійний аналіз передбачає використання для заключного аналізу ортогонального експерименту. Це означає, що оцінки відгуків у межах аналізу мають бути некорельованими. На практиці ортогональність гарантує використання тих самих випадкових послідовностей чисел під час виконання експериментів у межах кожної комбінації рівнів обробки.

Повний факторний експеримент

Експеримент, в якому реалізуються всі можливі сполучення рівнів факторів, називається повним факторним експериментом. Розглянемо простий двофакторний експеримент з одним фактором на двох рівнях, одним фактором на трьох рівнях і з двома спостереженнями в кожному досліді, тобто план 3x2 Запишемо в табл. 1 матрицю експерименту.
Таблиця 1. Матриця двофакторного експерименту

Фактор А	Фактор В
	Рівень 1	Рівень 2
Рівень 1	y111 y112	y121 y122
Рівень 2	Y211 y212	y221 y222
Рівень 3	y311 y312	y321 y322

У загальному випадку: значення фактора yijg, де g - номер спостереження, і та j - номери рівнів факторів А та В відповідно. Нехай математичне сподівання вихідної змінної М(уijg) – nij Тоді очікувану функцію відгуку можна записати у такому вигляді:

[math]{{y}_{ijg}}={{\eta }_{ij}}+{{e}_{ijg}},i=\overline{1,I};j=\overline{1,J};g=1,2,3,...,[/math] (1)
де eijg, - похибка досліду (або шум), яка вважається незалежною нормально розподіленою випадковою величиною з математичним сподіванням нуль і диспер¬сією σ2, або
[math]{{e}_{ijg}}=HHP(0,{{\sigma }^{2}}).[/math] (2)
Покажемо, що моделі для планування експериментів є окремими випадками моделей лінійної регресії [21]. Знайдою середнє за всіма дослідами:
[math]\mu =\frac{\sum\limits_{i\in I}^{{}}{{}}\sum\limits_{i\in I}^{{}}{{{\eta }_{ij}}}}{IJ}=\eta,[/math] (3)
де крапка означає усереднення по всіх значеннях відповідного індексу. Якщо знайти середнє значення відгуку для фактора А на рівні і з усіма рівнями фактора В, то
[math]{{A}_{i}}=\frac{\sum\limits_{j\in J}^{{}}{{{\eta }_{ij}}}}{J}={{\eta }_{i\bullet }}.[/math](4)
Тоді αAi, - головний ефект фактора А на рівні і визначається як різниця між його середнім і загальним середнім:
[math]\alpha _{i}^{A}={{A}_{i}}-\mu ={{\eta }_{j}}-\eta .[/math] (5)
З виразів (3)-(5) видно, що середнє головного ефекту дорівнює нулю, тому що
[math]\sum\limits_{i=1}^{I}{\alpha _{i}^{A}=\frac{1}{J}\sum\limits_{i}{\sum\limits_{j}{{{\eta }_{ij}}-\sum\limits_{i}{\mu =I\mu -I\mu =0}}}}.[/math] (6)
Головний ефект фактора В на рівні j визначаємо як
[math]\alpha _{j}^{B}={{B}_{j}}-\mu =\frac{1}{I}\sum\limits_{i}{{{\eta }_{ij}}-\mu =\eta -\eta.}[/math] (7)
Аналогічно
[math]\sum\limits_{j=1}^{J}{\alpha _{j}^{\beta }=0.}[/math] (8)
Якщо припустити, що фактори не взаємодіють між собою, то одержимо таку модель для планування проведення експерименту:
[math]M({{y}_{ijg}})={{\eta }_{ij}}=\mu +\alpha _{i}^{A}+\alpha _{j}^{B}.[/math] (9)
З виразу (9) маємо
[math]{{\eta }_{i1}}-{{\eta }_{i2}}=\alpha _{1}^{B}-\alpha _{2}^{B}.[/math] (10)
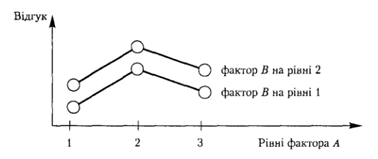
Вираз (10) є вірним для всіх рівнів і фактора А. Відобразивши графічно, як фактор А впливає на рівень і фактора В, одержимо паралельні криві відгуку (рис. 1). Якщо є взаємодія між факторами А \ В, то змі¬на фактора А викликає різноманітні зміни відгуку на різних рівнях фактора В. Таку взаємодію між рівнями і та j факторів А, В відповідно визначаємо як
[math]\alpha _{ij}^{AB}={{\eta }_{ij}}-{{A}_{i}}-{{B}_{j}}+\mu ={{\eta }_{ij}}-{{\eta }_{i}}-{{\eta }_{j}}+\eta .[/math] (11)

Рис.1 - Графік впливів факторів

Аналогічно, як було у виразах (6) і (8), маємо:

[math]\alpha _{j}^{AB}=\alpha _{i}^{AB}.[/math]

Тоді загальна модель з урахуванням взаємодії двох факторів буде такою:

[math]M({{y}_{ijg}})={{\eta }_{ij}}=\mu +\alpha _{i}^{A}+\alpha _{j}^{B}+\alpha _{ij}^{AB}.[/math] (12)

Верхні індекси позначають фактори, що взаємодіють між собою, а нижні - рівні, для яких визначається ефект. Покажемо, що модель факторного експерименту с окремим випадком рівнян¬ня регресії. Для простоти будемо вважати, що немає взаємодії між факторами і повторень дослідів. Використовуючи вирази (1) і (9), отримаємо систему рівнянь

[math]\begin{align} & {{y}_{11}}=\mu +\alpha _{1}^{A}+\alpha _{1}^{B}+{{e}_{11}}; \\ & {{y}_{12}}=\mu +\alpha _{1}^{A}+\alpha _{2}^{B}+{{e}_{12}}; \\ & ... \\ & {{y}_{32}}=\mu +\alpha _{3}^{A}+\alpha _{3}^{B}+{{e}_{32}}; \\ \end{align}[/math] (13)

яку в матричному вигляді можна записати так:

[math]{Y}=X{\beta }+{e},[/math] (14)

де

[math]{{{Y}}^{T}}=[{{y}_{11}},{{y}_{12}},...,{{y}_{32}}],[/math] (15)

X- матриця причинних або незалежних (фіктивних) факторів:

[math]X=\left[ \begin{matrix} 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 1 \\ \end{matrix} \right],[/math] (16)

де перший стовпчик - це значення µ, другий, третій і четвертий – αAi п'ятий і шостий - αβi, і = 1, 2, 3; j = 1, 2; - вектор ефектів або параметрів. Транспонований вектор

[math]{{{\beta }}^{T}}=[\mu ,\alpha _{1}^{A},\alpha _{2}^{A},\alpha _{3}^{A},\alpha _{1}^{B},\alpha _{2}^{B}].[/math] (17)

Вектор помилок:

[math]{{{e}}^{T}}=[{{e}_{11}},{{e}_{12}},...,{{e}_{32}}].[/math] (18)

На основі виразів (6) і (8) отримаємо двосторонні умови:

[math]\alpha _{1}^{A}+\alpha _{2}^{A}+\alpha _{3}^{A}=0;[/math](19)

[math]\alpha _{1}^{B}+\alpha _{2}^{B}=0.[/math] (20)

Обмеження (19) і (20) разом із так званими нормальними рівняннями вигляду

[math]{{X}^{T}}{Y}={{X}^{T}}X{\beta }[/math] (21)

дають лише одні оцінки МНК. З регресійного аналізу відомо, що у разі справедливості виразу (11) ці оцінки одночасно будуть і оцінками максимальної правдоподібності, а також лінійними незміщеними оцінками з мінімальними значеннями дисперсії. Таким чином, моделі факторних планів - це окремий випадок загальної лінійної регресійної моделі Вектор параметрів β містить сумарне середнє, головні ефекти і взаємодії; матриця незалежних змінних X складається лише з двох значень – 0 і 1 (використовують також позначення +1 та-1. або просто символи «+» і «-»). Отже, планування експерименту означає, що X вибирається таким чином, щоб оцінки мали деякі бажані властивості.

Дворівневий факторний план

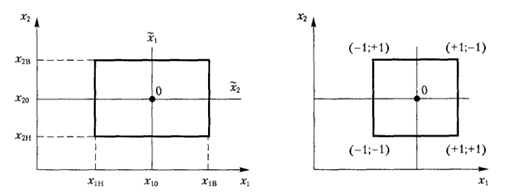
Повний факторний експеримент передбачає реалізацію всіх можливих комбінацій рівнів факторів. У найпростішому випадку значення факторів задають на двох рівнях. За наявності к факторів, загальна кількість комбінацій буде 2k. Розглянемо графічну інтерпретацію факторного експерименту (рис.2). Вважатимемо, що нижньому рівню фактора відповідає значення -1. верхньому +1, а основному – 0. Виконати подібне перетворення можна так:

[math]{{\widetilde{x}}_{i}}=\frac{({{x}_{i}}-{{x}_{i0}})}{ x},i=\overline{1,k}.[/math]

Рис.2 - Графічне зображення плану 22

Розглянемо результати проведення експериментів, зведені в табл. 2.

Таблиця 2. План дворівневого факторного експерименту

Фактор А	Фактор В
	Рівень 1	Рівень 2
Рівень 1	y111 y112	y121 y122
Рівень 2	Y211 y212	y221 y222

На основі даних табл. 2 можна записати таку систему рівнянь:

[math]\begin{align} & {{y}_{11}}=\mu +\alpha _{1}^{A}+\alpha _{1}^{B}+\alpha _{11}^{AB}+{{e}_{11}}; \\ & {{y}_{12}}=\mu +\alpha _{1}^{A}+\alpha _{2}^{B}+\alpha _{12}^{AB}+{{e}_{12}}; \\ & {{y}_{21}}=\mu +\alpha _{2}^{A}+\alpha _{1}^{B}+\alpha _{21}^{AB}+{{e}_{21}}; \\ & {{y}_{22}}=\mu +\alpha _{2}^{A}+\alpha _{2}^{B}+\alpha _{22}^{AB}+{{e}_{22}}; \\ \end{align}[/math] (22)

Оцінки параметрів моделі (22) за МНК можна знайти з урахуванням додаткових умов, які випливають із виразів (6), (8) і (11). Тоді отримаємо:

[math]\alpha _{1}^{A}=\alpha _{2}^{A};[/math] (23)

[math]\alpha _{1}^{A}=\alpha _{2}^{A};[/math] (24)

[math]\alpha _{21}^{AB}=\alpha _{11}^{AB};[/math] (25)

[math]\alpha _{21}^{AB}=\alpha _{11}^{AB};[/math](26)

[math]\alpha _{22}^{AB}=-\alpha _{21}^{AB}=\alpha _{11}^{AB};[/math] (27)

Підставивши вирази (23)-(27) у вираз (22), отримаємо систему рівнянь:

[math]\begin{align} & {{y}_{11}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{11}}; \\ & {{y}_{12}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{12}}; \\ & {{y}_{21}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{21}}; \\ & {{y}_{22}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{22}}; \\ \end{align}[/math] (28)

Запишемо систему рівнянь (28) у матричному вигляді

[math]{Y}=X{\beta }+{e,}[/math] (29)

[math]{{{Y}}^{T}}=({{y}_{11}},{{y}_{12}},{{y}_{21}},{{y}_{22}}),[/math] (30)

[math]X=\left[ \begin{matrix} +1 & -1 & -1 & +1 \\ +1 & -1 & +1 & -1 \\ +1 & +1 & -1 & -1 \\ +1 & +1 & +1 & +1 \\ \end{matrix} \right],[/math] (31)

[math]{{{\beta }}^{T}}=(\mu ,\alpha _{2}^{A},\alpha _{2}^{B},\alpha _{11}^{AB}),[/math] (32)

[math]{{{e}}^{T}}=({{e}_{11}},{{e}_{12}},{{e}_{21}},{{e}_{22}}).[/math] (33)

Зауважимо, що стовпчики матриці X - ортогональні, тобто

(34)

де і ) - будь-які два стовпчики матриці X. Очевидно, що X - невироджена матриця. Отже, оцінки МНК вектора такі: (35) З виразу (34) і за умови, що

[math]{x}_{i}^{T}{{{x}}_{j}}=0,(i\ne j),[/math] (36)

де N - число дослідів (у нашому випадку N = 4), отримаємо

[math]({{X}^{T}}X)=NI,[/math] (37)

де І - одинична матриця. Тоді деякий h-й елемент ХT визначається як

[math]\sum\limits_{g=1}^{N}{{{x}_{gh}}{{y}_{g}},(h=\overline{1,H})},[/math] (38)

де Xgh – g-й елемент вектора  ; Н - загальне число параметрів (у даному випадку чотири). Підставимо вирази (37) і (38) у вираз (35). Тоді

[math]{{b}_{n}}=\frac{1}{N}\sum\limits_{g=1}^{N}{{{x}_{gh}}{{y}_{g}}.}[/math] (39)

Звідси

[math]{{b}_{1}}=\widehat{\mu }=\frac{1}{4}({{y}_{11}}+{{y}_{12}}+{{y}_{21}}+{{y}_{22}})=y[/math] (41)

Порівняємо вираз (41) з визначенням головного ефекту :

[math]\alpha _{2}^{A}=\eta -\eta.[/math] (42)

Як бачимо, оцінка головного ефекту співпадає зі значенням самого ефекту. Таким самим способом можна показати, що оцінки за МНК головного ефекту і ефекту взаємодії утворюються просто за аналогією з їхніми визначеннями (7) і (11). Зверніть увагу, в матриці X перший стовпчик стосується тільки сумарного середнього ц і містить лише одиниці зі знаком плюс. Другий та третій стовпчики відповідають головним ефектам і факторів А і В відповідно. Елемент g (g= ) цих стовпчиків приймає значення – 1, якщо фактор знаходиться на нижньому рівні, та +1 на верхньому рівні. Для якісних факторів нижній і верх¬ній рівні є лише мнемонічними символами. Четвертий стовпчик матриці X показує результат взаємодії двох факторів . Елементи цього стовпчика - добуток елементів другого і третього стовпчиків Тоді регресій ну модель можна записати як

[math]{{y}_{g}}={{\beta }_{0}}+\sum\limits_{s=1}^{2}{{{d}_{gs}}{{\beta }_{s}}+({{d}_{g1}}{{d}_{g2}}){{\beta }_{12}}+{{e}_{g}},g=\overline{1,N}},[/math] (43)

де dgs, – -1. якщо фактор S в g-му досліді приймає значення нижнього рівня і dg, – +1 – у протилежному випадку. β0- загальне середнє µ; βs – головний ефект S-го фактора (наприклад, ); β12 ефект взаємодії двох факторів () Рівняння (43) - це повний поліном другого степеня без квадратичних членів (немає членів ).

Факторний план 2k

Розглянемо факторний план для випадку, коли k = 3 (табл 3).

Таблиця 3. Матрица повного факторного експерименту 2k

Комбінації	Фактори				Відгук
факторів	А	В		С
1	-1	-1		-1	1
2	+1	-1		-1	a
3	-1	+1		-1	b
4	+ 1	+1		-1	ab
5	-1	-1		+ 1	с
6	+1	-1		+ 1	ас
7	-1	+ 1		+ 1	bc
8	+1	+1		+ 1	abc

Для k факторів стовпчик S-го фактора (s = ) містить спочатку 2r-1 значень -1, потім 2s-1 значень +1, 2s-1 значень -1 і т. д. Відгук системи визначається згідно з наступним правилом: якщо в досліді фактор А приймає значення верхнього рівня, то у відгуку символ а присутній, як¬що нижнього рівня - відсутній Аналогічно обчислюється відгук для всіх інших факторів. Значення +1 у таблиці показує, що в даному досліді фактор приймає значення верхнього рівня, а - 1 - нижнього. Загальне число дослідів N = 2k. З матриці плану очевидно, що в одній половині дослідів фактор А приймає значення верхнього рівня, а в іншій - нижнього. Оцінка головного ефекту факто¬ра А обчислюється за формулою

[math]{{\widehat{\alpha }}^{A}}=\frac{\sum\limits_{i}{{{y}_{i}}}}{\tfrac{N}{2}}-\frac{\sum\limits_{j}{{{y}_{j}}}}{\tfrac{N}{2}}.[/math]

(44)

У цьому виразі індекс і відповідає відгукам для тих комбінацій факторів, при яких фактор А приймає значення на верхньому рівні, а; - відповідно на нижньому. Тому вираз (44) еквівалентний виразу

[math]{{\widehat{\alpha }}^{A}}=\frac{2}{N}\left\{ \sum\limits_{i}{(+1){{y}_{i}}+\sum\limits_{j}{(-1){{y}_{j}}}} \right\}=\frac{2}{N}\sum\limits_{g=1}^{N}{{{x}_{g1}}{{y}_{g}},}[/math]

де xg1 - g-й елемент стовпчика 1-го фактора У загальному випадку оцінка голов¬ного ефекту фактора s має такий вигляд:

[math]{{\widehat{\alpha }}^{s}}=\frac{2}{N}\sum\limits_{g=1}^{N}{{{x}_{gs}}{{y}_{g}}},(s=\overline{1,k}).[/math] (45)

Можна показати, що аналогічно виразам (22) – (42) оцінка у виразі (45) – це оцінка за методом найменших квадратів головного ефекту фактора s. Можна довести, що оцінки за методом найменших квадратів для ефекту взаємодії факторів j, m, r визначаються як

[math]{{\widehat{\alpha }}^{j,m,...,r}}=\frac{2}{N}\sum\limits_{g=1}^{N}{({{x}_{gj}}{{x}_{gm}}...{{x}_{gr}}){{y}_{g}}.}[/math] (46)

Оцінки загального середнього за методам найменших квадратів обчислюються за формулою

[math]\widehat{\mu }=\overline{y}=\frac{1}{N}\sum\limits_{g=1}^{N}{{{x}_{g0}}{{y}_{g}},}[/math] (47)

де

[math]{{x}_{g0}}=1,g=\overline{1,N}.[/math]

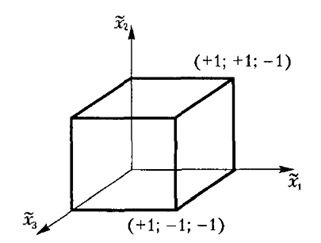
Факторний експеримент 2k містить 2k комбінацій факторів або точок експерименту в k-вимірному просторі з координатами ±1,як зображено на рис. 1.

Рис.3 - Графічне зображення плану 23

Якщо позначити число дослідів через N, то можна визначити матрицю плану.

[math]D=\{{{d}_{ij}}\},(i=\overline{1,N};j=\overline{1,k}),[/math]

де dij= -1, якщо j-й фактор приймає значення на нижньому рівні в і-й комбінації. Після додавання стовпчика з одних одиниць і всіх стовпчиків добутків шуканих факторів одержимо з матриці D матрицю незалежних змінних X. Наведемо матриці D і X (табл. 4) для випадку, коли к = 3, в яких опущено одиниці.

Таблиця 4. Матриці плану і незалежних змінних

Матриця плану D

Матриця незалежних змінних X

1

2

3

I

1

2

3

12

13

23

123

–

–

–

+

–

–

–

+

+

+

-

+

–

–

+

+

–

–

–

–

+

+

–

+

–

+

–

+

–

–

+

–

+

+

+

–

+

+

+

–

+

–

–

–

–

–

+

+

–

–

+

+

–

–

+

+

–

+

+

+

–

+

–

–

–

–

–

+

+

+

–

+

+

–

+

+

–

+

+

+

+

+

+

+

+

+

+

+

Загальне середнє, головні ефекти та всі ефекти взаємодії можна оцінити, якщо помножити відповідний стовпчик матриці X на стовпчик спостереження У. Рівняння регресії з k факторами на двох рівнях тоді записується так:

[math]\begin{align} & {{y}_{i}}=\sum\limits_{j=1}^{J}{{{x}_{ij}}{{\gamma }_{j}}+{{e}_{i}}={{\beta }_{0}}+\sum\limits_{s=1}^{k}{{{d}_{is}}{{\beta }_{s}}+\sum\limits_{s=1}^{k-1}{\sum\limits_{z=s+1}^{k}{({{d}_{is}}{{d}_{iz}}){{\beta }_{sz}}+}}}} \\ & +\sum\limits_{s=1}^{k-2}{\sum\limits_{z=s+1}^{k-1}{\sum\limits_{\upsilon =z+1}^{k}{({{d}_{is}}{{d}_{iz}}{{d}_{i\upsilon }}){{\beta }_{sz\upsilon }}+...+}}}({{d}_{i1}}{{d}_{i2}}...{{d}_{ik}}){{\beta }_{123}}...k+{{e}_{i}}, \\ \end{align}[/math]

де xij і dij – елементи матриць X, D відповідно; J = 2к – число параметрів регресії уj. Ці параметри позначають загальне середнє β0. головний ефект βs ефекти двофакторної взаємодії β s2 .., ефекти взаємодії k факторів β12…k .

Дробовий дворівневий факторний експеримент

Планування експерименту звичайно застосовується для визначення важливих факторів, що істотно впливають на відгук (відсівний експеримент). Враховуючи те. що із зростанням числа факторів кількість комбінацій факторів швидко збільшується, необхідно виділити найбільш важливі фактори, тобто попередньо відсіяти незначущі фактори. Для цього використовуються плани порядку 2 k-р, коли ефекти взаємодії більш високого порядку приймаються рівними нулю (вважається, що поліном низького порядку дасть адекватне регресійне рівняння). Кількість дослідів у повному факторному експерименті значно перевищує кількість обумовлених коефіцієнтів лінійної моделі головного експерименту, тобто повний факторний експеримент є надмірним. Якщо припустити, що деякі ефекти в цих планах є нульовими, то для побудови моделі знадобиться менше ніж 2к дослідів. Щоб зробити такий вибір, необхідно знайти, до яких наслідків призведе відкидання деяких дослідів Розглянемо приклад повного факторного експерименту 23 (табл.5).

Таблиця 5. Матриця повного факторного експерименту 23

№ Досліду	Матриця незалежних зміних X
	I	1	2	3	12	13	23	123	М( )
1	+	–	–	–	+	+	+	–	1
2	+	+	–	–	–	–	+	+	а
3	+	–	+	–	–	+	–	+	b
4	+	+	+	–	+	–	–	–	аb
5	+	–	–	+	+	–	–	+	с
6	+	+	–	+	–	+	–	–	ас
7	+	–	+	+	–	–	+	–	bс
8	+	+	+	+	+	+	+	+	аbс

Припустимо, що проведено лише чотири досліди, для яких

x1x2х3 = +1.

Тоді викреслимо із плану 1-й, 4-й. 6-й, 7-й рядки (отримаємо табл. 6) і покажемо. як обчислити оцінки ефектів парної взаємодії із неповного факторного експерименту для чотирьох дослідів, що залишились. Наприклад, для стовпчика І отримаємо оцінку головного ефекту

[math]{{\widehat{\alpha }}^{A}}=\frac{2}{N}({{y}_{2}}-{{y}_{3}}-{{y}_{5}}+{{y}_{8}}),[/math] (48)

де число дослідів N = 4.

Таблиця 6. Неповний факторний експеримент (x1 x2 х3 =+ 1 )

№	Матриця незалежних змінних X								M(y)
Досліду	I	1	2	3	12	13	23	123
2	+	+	–	–	–	–	+	+	а
3	+	–	+	–	–	+	–	+	b
5	+	–	–	+	+	–	–	+	с
8	+	+	+	+	+	+	+	+	abc

З формули (48) видно, що фактор знаходиться на верхньому рівні в дослідах 2 і 8. а на нижньому рівні - в дослідах 3 і 5. Звідси ефект фактора А:

[math]\frac{a+abc}{2}-\frac{b-c}{2}=\frac{1}{2}(a+b-c+abc).[/math]

Розглянемо тепер стовпчик , з якого одержуємо:

[math]{{\widehat{\alpha }}^{BC}}=\frac{2}{N}({{y}_{2}}-{{y}_{3}}-{{y}_{5}}+{{y}_{8}}).[/math] (49)

Взаємодія між двома факторами, що мають два рівні, визначиться таким чином. Якщо фактор С приймає значення верхнього рівня, то ефект фактора В ви¬значається як

[math]{{\eta }_{22}}={{\eta }_{12}},[/math] (50)

а якщо фактор С приймає значення нижнього рівня, то ефект фактора В відповідно буде

[math]{{\eta }_{21}}-{{\eta }_{11}}.[/math] (51)

Взаємодія між факторами В і С матиме місце тільки у випадку, якщо значення виразів (50) і (51) будуть різні. Тоді взаємодія визначатиметься як «середня» різниця між (50) і (51), а саме:

[math]{{\alpha }^{BC}}=\frac{1}{2}\left[ ({{\eta }_{22}}-{{\eta }_{12}})-({{\eta }_{21}}-{{\eta }_{11}}) \right],[/math]

тобто ефект взаємодії між факторами В і С – це середнє арифметичне різниці значень ефектів В і С на їх верхніх і нижніх рівнях відповідно. Ефект взаємодії між факторами В і С, за умови що фактори В і С знаходяться на верхньому та нижньому рівнях відповідно, можна визначити як abc - с. Якщо фактор С приймає значення на нижньому рівні, ефект В можна оцінити як b а Половина різниці між цими ефектами становить

[math]\frac{1}{2}(abc-c)-(b-a)=\frac{1}{2}(abc-c-b+a).[/math] (52)

Порівняємо вирази (49) і (48). Маємо такі ж оцінки дія ал і вeC. Або іншим шляхом це можна показати. використовуючи останній стовпчик табл. 6:

[math]M({{y}_{2}}-{{y}_{3}}-{{y}_{5}}+{{y}_{8}})=a-b-c+abc.[/math] (53)

Запишемо праву частину виразу (53) як

[math]\begin{align} & a-b-c+abc=\frac{2}{N}(-1+a-b+ab-c+ac-bc+abc)+ \\ & +\frac{2}{N}(+1+a-b-ab-c-ac+bc+abc) \\ & \\ \end{align}[/math]

при N = А, або, враховуючи вирази (45) і (46), як

[math]a-b-c+abc={{\alpha }^{A}}+{{\alpha }^{BC}}.[/math] (54)

Об'єднавши вирази (53) і (54), отримуємо

[math]M({{y}_{2}}-{{y}_{3}}-{{y}_{5}}+{{y}_{8}})={{\alpha }^{A}}+{{\alpha }^{BC}}.[/math]

Із дробового факторного експерименту в цьому прикладі випливає, що мають місце однакові значення для головного ефекту фактора А та ефекту взаємодії факторій В і С. Не так звані змішані ефекти або ефекти, що оцінюються спільно. Якщо ефект взаємодії дорівнює нулю, значення виразу (у2 – y3 – y5 +y8) буде незміщеною оцінкою αA головного ефекту фактора А. Таким чином, для побудови плану 2k відкидаємо ті рядки з повного факторного експерименту, що мають значення +1 дія деякого ефекту. Це так звані напіврепліки, тобто тут використовується половина повного факторного експеримен¬ту. Аналогічно, для другої напіврепліки необхідно відкинути ті рядки, які мають значення -1 для деякого ефекту. При великій кількості факторів k навіть напіврепліки (тобто плани 2k-1) можуть виявитись занадто громіздкими. У цих планах деякі ефекти взаємодії високого порядку можна прирівняти до нуля, та взяти меншу частину від повного факторного експерименту. Репліки, що становлять (1/2)p частину повного факторного плану з k факторами, називають планом типу 2k-p Плани можна застосовувати послідовно, тобто спочатку одержати спостереження для одних комбінацій рівнів факторів, потім для інших і після аналізу цих спостережень вирішити, для якої комбінації (старої або нової) слід провести додаткові спостереження. Нові спостереження знову аналізуються (звичайно разом з попередніми) для ухвалення рішення про подальші спостереження і т. д У планах 2k-p можна спочатку провести частину експерименту, проаналізувати спостереження, і якщо цей аналіз покаже, то дана частина експерименту занадто мала для оцінки всіх можливих ефектів, експеримент розширюють таким чином, щоб він дав змогу оцінити вплив усіх факторів.

Список використаних джерел

1. Моделювання систем - Томашевский В.М.:BHV, 2005. – 352с.
2. Аністратенко В.О., Федоров В.Г. Математичне планування експерименту в АПК. К.: Вища школа, 1993. – 375 с.
3. Теория эксперимента: Курс лекций. - А, В. Блохин. - Мн.: БГУ, 2002. - 67 с.

Студент: Користувач:Залецький Михайло

Виступ відбувся: 17 лютого 2010

Тема: Регресійні моделі при повному 2 дробовому факторному експерименті. Визначення коефіцієнтів регресії