Швидкість звуку у рідинах
Швидкість звуку - швидкість розповсюдження пружних хвиль у середовищі - як поздовжніх у газах, рідинах і твердих тілах, так і поперечних (зсувних) у твердім середовищі. Визначається пружністю і щільністю середовища. Швидкість звуку в газах, рідинах і ізотропних твердих середовищах зазвичай є незмінною для даної речовини. Як правило, у газах швидкість звуку менша, ніж в рідинах, а в рідинах швидкість звуку менша, ніж у твердих тілах, тому при зріджуванні газу швидкість звуку зростає. У широкому розумінні звукові хвилі — це будь-які механічні хвилі (тобто хвилі в пружних середовищах). У вузькому значенні звук — це такі пружні хвилі, дія яких створює у людини слухові відчуття. Більшість людей чує звуки, яким відповідають частоти коливань від 16÷20 Гц до 20 кГц. Більш низькі частоти відповідають інфразвуку, а більш високі — ультразвуку. Швидкість звуку в речовинах визначається їх пружністю і густиною й обчислюється за формулою:
[math]\ v = \sqrt {\frac{E}{\rho }} \[/math],
де E — модуль Юнга,[math]\ \rho \[/math] — густина. Швидкість звуку мінімальна у газах (за нормальних умов у повітрі[math]\ v = 330 - 340 \[/math]м\с ,залежно від температури: чим більше значення T, тим більша швидкість; максимальна у твердих тілах[math]\ v = 6000\frac{}{} \[/math]м/с (у сталях ); рідини займають проміжне положення[math]\ v = 1500\frac{}{} \[/math]м\с (у воді ). У динаміці рідини , швидкість звуку в рідкому середовищі (газ або рідина) використовується як відносна міра своєї власної швидкості. Швидкість (на відстані в одиницю часу), поділена на швидкість звуку в рідині називається числом Маха. Об'єкти, які рухаються із швидкістю більшою, ніж Mach 1 рухаються на надзвукових швидкостях. Швидкість звуку в ідеальному газі не залежить від частоти, але слабо залежить від частоти для всіх реальних фізичних процесах. Це функція квадратного кореня від температури, але майже не залежить від тиску і щільності для даного газу. Для різних газів, швидкість звуку залежить від квадратного кореня із середньої молекулярної маси газу, в якій молекули газу можуть зберігати тепло від стиснення , тому що звук у газах тип стиснення. Хоча, у випадку газів тільки, швидкість звуку може бути виражена в термінах відносних як щільність і тиск, ці величини не є повністю незалежними один від одного. У твердих тілах, звукові хвилі поширюються у вигляді двох різних типів. Поздовжня хвиля пов'язана з компресією і декомпресією в напрямку руху, той же процес, як і поширення звукових хвиль у газах і рідинах. Поперечної хвилі,характеризуються пружною деформацією середовища перпендикулярно напрямку руху хвилі; напрямок зсуву деформації називається "поляризація" даного типу хвиль. Загалом, поширення поперечних хвиль відбуваються в парі ортогональних поляризацій. Ці різні хвилі (хвилі стиснення і різної поляризації поперечних хвиль) можуть мати різні швидкості на тій же частоті. Таким чином, вони досягають спостерігача в різний час, можливий приклад час землетрусу , де хвилі стиснення прибувають першими, а хитання поперечних хвиль на кілька секунд пізніше.
Швидкість пружних хвиль у будь-якому середовищі визначається стисливістю та щільністю. Швидкість поперечних хвиль , які можуть виникнути тільки в твердих тілах, визначається твердістю матеріалу жорсткістю, щільністю і стисненням.
Зміст
Історична довідка
- Звуки почали вивчати ще в далекій давнині. Перші спостереження з акустики були проведені в VI столітті до нашої ери. Піфагор встановив зв'язок між висотою тону і довжиною струни або труби видавати звуки.
- У IV ст. до н.е. Аристотель першим правильно уявив, як поширюється звук у повітрі. Він сказав, що звучить тіло викликає стискання і розрідження повітря і пояснив луну відбиттям звуку від перешкод.
- У XV столітті Леонардо да Вінчі сформулював принцип незалежності звукових хвиль від різних джерел.
- В 1660 році в дослідах Роберта Бойля було доведено, що повітря є провідником звуку (в вакуумі звук не поширюється).
- Саверіо, дав перший розрахунок довжини хвилі звуку і прийшов до висновку, добре відомому зараз у фізиці, що для будь-якої відкритої труби довжина хвилі випускається звуку дорівнює подвоєною довжині труби. "І в цьому складаються найголовніші звукові явища".
- Після експериментальних досліджень Саверіо до математичного розгляду задачі про коливається струні в 1715 році приступив англійський математик Брук Тейлор, поклавши цим початок математичної фізики у власному розумінні слова. Йому вдалося розрахувати залежність числа коливань струни від її довжини, ваги, натягу та місцевого значення прискорення сили тяжіння. Це завдання відразу ж стала широко відома і привернула увагу майже всіх математиків XVIII століття, викликавши довгу і плідну дискусію. Нею займалися серед інших Йоганн Бернуллі та його син Данило Бернуллі, Ріккаті і Даламбер. Останній знайшов рівняння з частинними похідними, що визначають малі коливання однорідної струни, і проінтегрувати їх методом, вживаним і понині. Але найбільш істотний внесок зробив Ейлер. Йому ми зобов'язані повною теорією коливань струни, початок побудови якої було покладено в 1739 році в його праці
- "Досвід нової теорії музики" і продовжувалося в численних подальших доповідях. Зокрема, з теорії Ейлера випливало, що швидкість поширення хвилі по струні не залежить від довжини хвилі збуджуваного звуку. Ейлер виробляв також теоретичні дослідження коливань стрижнів, кілець, дзвонів, але отримані результати не збіглися з результатами експериментальної перевірки, здійсненої німецьким фізиком Ернестом Флорес Фрідріхом Хладні, якого вважають батьком експериментальної акустики. Хладні першим точно досліджував коливання камертона і в 1796 році встановив закони коливань стрижнів.
- Фактичне пояснення луни, явища досить примхливого, також належить Хладні, принаймні в істотних частинах. Йому ми зобов'язані і новим експериментальним визначенням верхньої межі чутності звуку, що відповідає 20 000 коливань у секунду. Ці вимірювання, неодноразово повторені фізиками до сих пір, вельми суб'єктивні й залежать від інтенсивності і характеру звуку. Але особливо відомі досліди Хладні в 1787 році по дослідженню коливань пластин, при яких утворюються красиві "акустичні фігури", що носять назви фігур Хладні і виходять, якщо посипати коливається платівку піском. Ці експериментальні дослідження поставили нове завдання математичної фізики - задачу про коливання мембрани.
- Хладні почав дослідження поздовжніх хвиль у твердих тілах і зіставив поздовжні і поперечні коливання стрижня при різних способах збудження (ударом, тертям та ін.) Дослідження поздовжніх хвиль були продовжені експериментально Саварен, а теоретично - Лапласом і Пуассоном.
- У XVIII столітті було досліджено багато інших акустичних явищ (швидкість поширення звуку у твердих тілах і в газах, резонанс, комбінаційні тону та ін.) Всі вони пояснювалися рухом частин вагається тіла і частинок середовища, в якому розповсюджується звук. Іншими словами, всі акустичні явища пояснювалися як механічні процеси.
- У 1787 році Хладні, основоположник експериментальної акустики відкрив поздовжні коливання струн, пластин, камертонів і дзвонів. Він першим досить точно виміряв швидкість поширення звукових хвиль в різних газах. Довів, що в твердих тілах звук поширюється не миттєво, а з кінцевою швидкістю, і в 1796 році визначив швидкість звукових хвиль у твердих тілах стосовно звуку в повітрі. Він винайшов ряд музичних інструментів. У 1802 році вийшла праця Ернеста Хладні "Акустика", де він дав систематичний виклад акустики.
- Після Хладні французький вчений Жан Батіст Біо в 1809 році вимірював швидкість звуку в твердих тілах.
- У 1816 році французький фізик П'єр Симон Лаплас вивів формулу для швидкості звуку в газах.
- У 1827 році Ж. Колладон і Я. Штурм провели досвід на Женевському озері з визначення швидкості звуку у воді, отримавши значення 1435 м/с.
Теорія
Звук в рідинах і газах
Звук в рідинах і газах описується рівннями Ейлера, неперервності і адіабатичного процесу.
[math]\ \frac{{\partial v}}{{\partial t}} + v(\nabla \cdot v) = - \frac{1}{\rho }\nabla p \[/math]
[math]\ \frac{{\partial \rho }}{{\partial t}} + div\rho v = 0 \[/math]
[math]\ pV^\gamma = const \[/math]
Тут [math]\ v \[/math] — швидкість змішення частинок, ρ — густина, p — тиск, γ — адіабатичний показник.
Поширення звуку — адіабатичний процес, бо воно відбувається швидше, ніж відбувається поширення тепла. Як наслідок, при проходженні звуку температура дещо зрозстає в областях стиску і спадає, при розширенні.
Вважаючи збурення при проходженні звуку малими, ця система рівнянь зводиться до хвильового рівняння
[math]\ \Delta p - \frac{1}{s}\frac{{\partial ^2 p}}{{\partial t^2 }} = 0 \[/math]
де
[math]\ s^2 = \left( {\frac{{\partial p}}{{\partial \rho }}} \right) \[/math]
Величина s визначає швидкість звуку.
Для ідеального газу
[math]\ s = \sqrt {\gamma \frac{{RT}}{m}} \[/math]
де R — газова стала, m — молярна маса.
Оскільки стисливість рідин менша, ніж газів, то швидкість звуку в них більша. Ті ж міркування справедливі для твердих тіл.
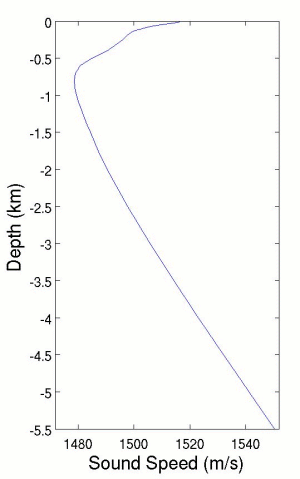
Швидкість звуку у воді
У чистій воді швидкість звуку становить 1 348 м / с. Прикладне значення також має швидкість звуку в солоній воді океану. Швидкість звуку збільшується в більш солоной і більш теплій воді. При більшому тиску швидкість також зростає, тобто чим глибше, тим швидкість звуку більша. Розроблено кілька теорій розповсюдження звуку у воді.Наприклад
- теорія Вільсона 1960 року для нульової глибини дає таке значення швидкості звуку:
c = 1449,2 + 4,623 (T) - 0,0546 (T2) + 1,39 (S - 35),
де c - швидкість звуку в метрах за секунду, T - температура в градусах Цельсія, S - солоність в проміле.
Іноді також користуються спрощеною формулою Лероя: c = 1492,9 + 3 (T - 10) - 0,006 (T - 10) 2 - 0,04 (T - 18) 2 + 1,2 (S - 35) - 0,01 (T - 18) (S - 35) + z / 61,
де z - глибина в метрах. Ця формула забезпечує точність порядку 0,1 м / с для T <20 ° C і z <8 000 м.
При температурі 24 ° C, солоності 35 проміле і нульовий глибині (пляж), швидкість звуку дорівнює близько 1 640 м / c. При T = 4 ° C, глибині 100 м і тієї ж солоності (підводний човен на завданні) швидкість звуку дорівнює 1 570 м / с [2].ї
Експерментальні методи визначення швидкості звуку
Ряд різних методів існують для вимірювання рівня звуку в повітрі. Найбільш ранні досить точні оцінки швидкості звуку в повітрі виступив Вільям Дерхам , і визнається Ісаак Ньютон . Дерхам був телескоп у верхній частині вежі церкви святого Лаврентія в Апмінстер , Англія. На спокійний день, синхронізовані кишеньковий годинник буде приділено помічник, який буде стріляти рушницю на заздалегідь визначений час з помітною точкою деякі миль, у сільській місцевості. Це може бути підтверджено за допомогою телескопа. Потім він виміряв інтервалу між бачачи Гансмок і прибуття шуму за допомогою півсекунди маятника. Відстані від місця пістолет був звільнений був знайдений тріангуляції, і простим поділом (час / відстань) за умови, швидкості. Нарешті, зробивши багато зауважень, з використанням цілого ряду різних відстанях, неточності півсекунди маятник може бути усереднені, даючи свою остаточну оцінку швидкості звуку. Сучасні секундоміри включити цей метод, який використовується сьогодні на відстані максимально коротким 200-400 метрів, і не потребують в той же голосно, як рушницю.
Покадрові методи
Найпростіша концепція вимірювання з використанням двох мікрофонів і швидко записуючого пристрою, такі як цифрові рамки зберігання. Цей метод використовує наступну думку.
Якщо джерело звуку і два мікрофони розташовані по прямій лінії, з джерела звуку на одному кінці, то наступний може бути виміряна: 1. Відстань між мікрофонами (х), називається основі мікрофона. 2. Час прибуття між сигналами (затримка), досягаючи різних мікрофонів (T)Тоді V = X /m
Інші методи
У цих методах час вимірювання була замінена виміру зворотного часу ( частота ).
в трубці Кундта приклад експерименту, який може бути використаний для вимірювання швидкості звуку в невеликому обсязі. Він має перевагу, що дозволяє вимірювати швидкість звуку в будь-який газ. Цей метод використовує порошок, щоб зробити вузли і пучності видно людському оку. Це приклад компактного експериментальної установки.
Камертону може бути проведений в гирлі довго труби який занурення в бочку з водою . У цій системі це справа, що труба може бути доведена до резонансу, якщо довжина повітряного стовпа в трубі дорівнює (1 +2 {N} λ / 4), де N є цілим числом. Як antinodal точкою для труб на відкритому кінці трохи за межами устя труби краще знайти двох або більше точок резонансу і потім виміряти половину довжини хвилі між ними.
Таблиці
В наступній таблиці представлено швидкість звуку в різних середовищах.
| Швидкості звуку в різних середовищах | |
| Речовина | Швидкість звуку, м/с |
| Повітря (при 20 °C)" | 343,1 |
| Вода | 1 483 |
| Водень | 1 284 |
| Гума | 1 800 |
| Дерево | 3 320 |
| Залізо | 5 850 |
| Морська вода | 1 530 |
При нормальних умовах залежність швидкості, а також густини повітря від температури можна представити наступною таблицею.
| θ в °C | s в м/с | ρ в кг/м3 | Z в N·с/м-3 |
| −10 | 325.2 | 1.342 | 436.1 |
| −5 | 328.3 | 1.317 | 432.0 |
| 0 | 331.3 | 1.292 | 428.4 |
| 5 | 334.3 | 1.269 | 424.3 |
| 10 | 337.3 | 1.247 | 420.6 |
| 15 | 340.3 | 1.225 | 416.8 |
| 20 | 343.2 | 1.204 | 413.2 |
| 25 | 346.1 | 1.184 | 409.8 |
| 30 | 349.0 | 1.165 | 406.3 |
Джерела
- Справочник по радиоэлектронике. — М., «Энергия», 1968;
- Фізика: Підр. для 9 кл. серед. шк.: Затв. Держ. ком. СРСР по нар. освіті. — К.: Рад. шк., 1990. — 208 с.: іл. [ISBN 5-330-00570-1];
- А. М. Федорченко Теоретична механіка, Київ: Вища школа, 1975., 516 с.;
http://en.wikipedia.org/wiki/Speed_of_sound#Speed_of_sound_in_liquids