Відмінності між версіями «Планування та проведення експериментів з моделями»
Zhunik (обговорення • внесок) (Створена сторінка: =Планування та проведення експериментів з моделями= Усяке наукове дослідження, що провод…) |
Zhunik (обговорення • внесок) |
||
| Рядок 20: | Рядок 20: | ||
Перелічимо основні проблеми, які виникають під час проведення експериментів з імітаційними моделями. | Перелічимо основні проблеми, які виникають під час проведення експериментів з імітаційними моделями. | ||
| − | + | 1. Визначення початкових умов проведення експерименту.<br> | |
Зазвичай експеримент починають, коли модель перебуває в стані «пусто і вільно», тобто в моделі немає динамічних об'єктів або транзактів і всі пристрої та ресурси вільні. Якщо розглядається досить тривалий період моделювання, то можна задати так званий період «розігріву» чи «розгону» моделі, або перехідний процес, після якого модель переходить у сталий (стаціонарний) режим роботи. Урахування даних перехідного процесу для оцінювання вихідних змінних моделі спричинює зміщення статистичних оцінок параметрів. | Зазвичай експеримент починають, коли модель перебуває в стані «пусто і вільно», тобто в моделі немає динамічних об'єктів або транзактів і всі пристрої та ресурси вільні. Якщо розглядається досить тривалий період моделювання, то можна задати так званий період «розігріву» чи «розгону» моделі, або перехідний процес, після якого модель переходить у сталий (стаціонарний) режим роботи. Урахування даних перехідного процесу для оцінювання вихідних змінних моделі спричинює зміщення статистичних оцінок параметрів. | ||
Щоб зменшити вплив вихідних даних перехідного процесу на кінцеві результати, моделювання слід починати з використання модальних (найбільш імовірних) або середніх значень сталого режиму. Такий спосіб запуску моделі забезпечує зменшення тривалості перехідного процесу моделі, але застосування даного способу ефективне лише в тому випадку, коли завантаження пристроїв обслуговування в моделі невелике. У разі наближення коефіцієнтів завантаження пристроїв до одиниці на виході моделі можна спостерігати стаціонарний процес, під час якого неможливо чітко визначити дані перехідного процесу (рис. 1). | Щоб зменшити вплив вихідних даних перехідного процесу на кінцеві результати, моделювання слід починати з використання модальних (найбільш імовірних) або середніх значень сталого режиму. Такий спосіб запуску моделі забезпечує зменшення тривалості перехідного процесу моделі, але застосування даного способу ефективне лише в тому випадку, коли завантаження пристроїв обслуговування в моделі невелике. У разі наближення коефіцієнтів завантаження пристроїв до одиниці на виході моделі можна спостерігати стаціонарний процес, під час якого неможливо чітко визначити дані перехідного процесу (рис. 1). | ||
| + | <center>[[Файл:PlanyvannyaEksperymentuPuc1.png]]<br> | ||
| + | Рис. 1. Стаціонарний процес виходу із СМО з близьким до одиниці коефіцієнтом завантаження</center> | ||
| + | |||
| + | У разі оцінювання статистичних параметрів вихідних величин рекомендується не враховувати дані перехідного процесу, оскільки вони можуть викликати істотне зміщення шуканих оцінок. Усунення зміщення досягається шляхом відкидання даних перехідного процесу (в мові GPSS це можна зробити, використавши команду RESET). Найскладнішим є встановлення моменту досягнення сталого стану системи. Досі не існує цілком надійних методів визначення цього моменту [4]. Однак дана проблема може бути вирішена за допомогою діалогових та інтелектуальних систем моделювання, які дають змогу контролювати і графічно відображати хід моделювання. Найефективніший спосіб визначення початку сталого режиму - це спостереження за графіками зміни вихідного процесу в часі (рис. 2). | ||
| + | <center>[[Файл:PlanyvannyaEksperymentuPuc2.png]]<br> | ||
| + | Рис. 2. Графіки вихідних даних моделі СМО</center> | ||
| + | |||
| + | 2. Зупинення процесу моделювання.<br> | ||
| + | Правила зупинення процесу моделювання дозволяють визначити тривалість прогону імітаційної моделі — а від цього залежить точність результатів. Наприклад, якщо потрібно провести моделювання роботи виробничої дільниці протягом робочого тижня, то час прогону моделі можна визначити саме цим терміном. Дослідник сам приймає рішення, чи буде досягнуто за вказаний період моделювання сталий режим роботи моделі. Він також обирає метод збирання вихідних даних і оцінювання точності результатів моделювання. Точність оцінювання параметрів системи в цьому випадку визначається за одним досить тривалим прогоном моделі. | ||
| + | Визначають два типи імітаційного моделювання — скінченне і нескінченне. Для першого процес моделювання закінчується, коли відбувається «природна» подія, яка дає змогу визначити тривалість прогону моделі. Така подія часто відбувається в той момент, коли система звільняється від вимог, чи в момент, після якого вже не можна одержати корисної інформації, або моделювання закінчується за показниками таймера. Така подія визначається до виконання прогонів моделі, її настання має бути детермінованою (згідно з таймером) або випадковою величиною. Оскільки початкові умови скінченного моделювання, як правило, впливають на критерії оцінювання, вони мають представляти умови, характерні для роботи реальної системи. | ||
| + | Під час виконання нескінченного імітаційного моделювання не існує події, настання якої давало б змогу визначати тривалість прогону моделі. Моделювання цього типу використовується у разі дослідження поведінки системи за умов сталого режиму її роботи протягом тривалого часу. Параметри, що оцінюються в цьому випадку, вважаються сталими, якщо вони залежать від характеристик сталих законів розподілів ймовірностей деякого вихідного процесу. | ||
| + | |||
| + | 3. Стан моделі в момент припинення прогону.<br> | ||
| + | Під час моделювання завжди виникає питання щодо доцільності використання динамічних компонентів, або транзактів, які залишилися в моделі після закінчення її роботи. Урахування характеристик цих компонентів може призвести до збільшення зміщення статистичних оцінок параметрів моделі. На приклад, під час моделювання роботи дільниці цеху було зроблено припущення, що найменш тривалі роботи виконуються в першу чергу. Тоді на момент закінчення моделювання може виникнути ситуація, коли в моделі залишаться тільки роботи, термін виконання яких великий. Якщо їх не враховувати, оцінка середньої тривалості виконання робіт у цеху буде заниженою. | ||
| + | |||
| + | 4. Визначення тривалості прогону моделі за наявності в ній процесів з різними швидкостями протікання.<br> | ||
| + | Для оцінювання точності результатів моделювання здебільшого використовують параметри найповільнішого процесу в моделі. У цьому випадку оцінки для більш швидких процесів будуть набагато кращими і ефективнішими, ніж для повільних, тобто довірчі інтервали для останніх будуть більшими. Під час розроблення імітаційної моделі обирають такий ступінь її деталізації, щоб швидкості процесів, які протікають у моделі, не відрізнялися більш ніж на два порядки. У разі необхідності моделювання рідких подій або повільних процесів, наприклад відмов устаткування, потрібно укрупнювати стани для швидких процесів. Для цього використовують аналітико-імітаційні моделі. | ||
| + | |||
| + | ==Оцінювання точності результатів моделювання== | ||
| + | Оцінити точність результатів моделювання можна шляхом побудови довірчих інтервалів для вихідних змінних (відгуків) моделі. Точність результатів залежить насамперед від кількості реалізацій (прогонів моделі) і тривалості прогону для кожної реалізації моделі. Якщо модель детермінована, то для отримання точних результатів моделювання достатньо одного прогону. У загальному випадку дані спостереження одного прогону моделі представляють одиничну вибірку або часовий ряд. Часовий ряд — це реалізація випадкового процесу. В результаті кожного прогону моделі утворюються часові ряди для кожного значення відгуку моделі досліджуваних випадкових процесів. | ||
| + | Під час моделювання стохастичних систем потрібно розглядати два режими роботи моделей: перехідний і стаціонарний. Стаціонарний режим визначається сталим процесом на виході моделі. Слід зазначити, що для більшості реальних систем характеристики стохастичних процесів, у тому числі й закони розподілу, з часом змінюються. За наявності нової інформації відносно параметрів системи потрібно повторно проаналізувати сталі параметри моделі. | ||
| + | ===Перехідний режим роботи моделі=== | ||
| + | Для більшості виробничих систем неможливо гарантувати, що вони працюватимуть у стаціонарному режимі. Винятком є системи роботизованого автоматичного виробництва. Якщо модель працює в перехідному режимі, то необхідну кількість прогонів моделі можна розрахувати за тими ж формулам, що і для методу статистичних випробувань; при цьому під час кожного прогону моделі з використанням однакових вхідних даних і параметрів формується своя послідовність випадкових чисел. Оскільки випадкові величини незалежні, то незалежними мають бути й отримані вихідні дані для кожного прогону моделі. Це дає змогу побудувати довірчий інтервал, скориставшись центральною граничною теоремою. Необхідну точність ɛ можна задати, наприклад, такою, що дорівнює ± 5 % середнього значення величини, для якої будується довірчий інтервал, якщо а = 0,05. | ||
| + | Після проведення прогонів моделі розраховуються оцінки загального середнього значення вихідної змінної та середньоквадратичного відхилення і будується довірчий інтервал для середнього значення. Більшість програмних засобів імітаційного моделювання забезпечують автоматичне проведення таких розрахунків. Наприклад, якщо модель реалізовано мовою GPSS World, то після останнього прогону достатньо викликати процедуру ANOVA, яка і побудує довірчі інтервали для вихідних змінних. | ||
| + | Якщо кількість прогонів невелика (менше ніж 30), то для побудови довірчого інтервалу використовують розподіл Стьюдента (t-розподіл). За наявності більшого числа прогонів для визначення значення ta можна використовувати нормальний розподіл. | ||
| + | Процедура повторних прогонів (реплікацій) має важливу властивість - незалежність вибірок. Ця властивість є універсальною і може застосовуватись для моделювання як перехідного, так і стаціонарного режиму роботи моделі. Слід зауважити, що в разі моделювання стаціонарного режиму ця процедура дає змогу зібрати дані й перехідного періоду, які не використовуються під час аналізу стаціонарного режиму. | ||
| + | |||
| + | ===Стаціонарний режим роботи моделі=== | ||
| + | Під час моделювання деяких систем, наприклад комп'ютерних та комунікаційних, виникає потреба аналізувати їх роботу в сталому, стаціонарному режимі. Існування такого режиму в системі дає змогу побудувати довірчий інтервал для оцінок параметрів за результатами не багатьох прогонів моделі, а лише одного, досить тривалого. | ||
| + | Основна проблема, пов'язана з побудовою довірчого інтервалу, обумовлена тим, що вихідні дані імітаційної моделі є корельованими. Крім того, наявність перехідних процесів у моделі призводить до зміщення статистичних оцінок. На жаль, не існує надійних методів виявлення моменту завершення перехідного періоду роботи моделі. Якщо критерієм оцінювання є вартісна характеристика (прибуток, витрати та ін.), яка визначається для стаціонарного режиму роботи моделі, тривалість прогону може бути визначена на основі результатів спостереження за зміною величини, що дорівнює відношенню оцінюваного показника за весь період моделювання до тривалості моделювання (наприклад, витрати за одиницю часу), для якої будують графік зміни в модельному часі. Оскільки тривалість перехідного періоду може змінюватись в залежності від комбінацій вхідних змінних моделі і послідовностей випадкових чисел, потрібно визначити найдовший перехідний період. Статистичні дані перехідного періоду роботи моделі не повинні враховуватись під час розрахунків статистичних оцінок для вихідних змінних. | ||
| + | Необхідно, щоб тривалість прогону відповідала сталому режиму функціонування моделі (рис. 3). На практиці діють таким чином. За графіком вихідної змінної моделі визначають час моделювання, коли закінчується перехідний період tпер. Статистичні дані, зібрані за цей період, не враховуються під час стати стичного аналізу. Наприклад, у мові GPSS це робиться за допомогою команди RESET, яка видаляє накопичені статистичні дані, але залишає транзакти в моделі, фіксує поточні значення довжин черг і максимальний вміст блоків STORAGE. Після цього повторно викликається команда START, що задає тривалість прогону моделі не меншою ніж 100tпер. | ||
| + | <center>[[Файл:PlanyvannyaEksperymentuPuc3.png]]<br> | ||
| + | Рис. 3. Визначення сталого режиму роботи моделі</center> | ||
| + | |||
| + | Розглянутий вище спосіб є наближеним, але він широко використовується на практиці. Існують інші методи, застосування яких дає змогу отримати більш надійні оцінки для характеристик стаціонарних процесів. У книзі А. Лоу і В. Келтона [2] описується шість методів для обчислення оцінки стаціонарного середнього випадкового процесу, серед яких основну увагу приділено методу реплікації і вилучення. | ||
| + | |||
| + | ==Особливості планування експериментів== | ||
| + | Послідовність дій, які необхідно виконувати під час планування експериментів. | ||
| + | # Визначення відгуків (вихідних змінних) системи. | ||
| + | # Визначення факторів, які впливають на відгук системи. Більшість систем підпорядковуються принципу Парето - з огляду на характеристики системи істотними є лише деякі з множини факторів. У більшості систем 20 % факторів визначають 80 % властивостей системи. | ||
| + | # Визначення рівнів факторів. Мінімальна кількість рівнів для кожного фактора два - нижня і верхня межі значення фактора. У разі використання цього числа рівнів можна визначити тільки лінійні ефекти. Для врахування квадратичних ефектів необхідно використовувати три рівні, для кубічних ефектів – чотири і т. д. Аналіз значно спрощується, якщо брати тільки рівновіддалені одне від одного значення рівнів. У цьому випадку маємо так зване ортогональне планування, або ортогональний експеримент.<br> | ||
| + | Для множинних експериментів з числом факторів більше одного дисперсійний аналіз передбачає використання для заключного аналізу ортогонального експерименту. Це означає, що оцінки відгуків у межах аналізу мають бути некорельованими. На практиці ортогональність гарантує використання тих самих випадкових послідовностей чисел під час виконання експериментів у межах кожної комбінації рівнів обробки. | ||
Версія за 13:08, 11 березня 2010
Зміст
Планування та проведення експериментів з моделями
Усяке наукове дослідження, що проводиться за допомогою моделі, передбачає планування та проведення експериментів, у ході яких збираються необхідні дані. Ці Дані підлягають аналізу, і на його основі визначають, чи можна під час моделювання досягти поставлених цілей. Якщо експеримент не сплановано належним чином, Існує небезпека того, що не буде отримано бажаних результатів або результати виявляться помилковими. Це може призвести до прийняття неправильних рішень чи необхідності повторного проведення експерименту (найбільш трудомістка операція) і навіть до перебудови моделі. Разом з тим повинна існувати можливість повторення іншими дослідниками експерименту, результати якого вважаються значущими.
Проблеми планування імітаційних експериментів
Імітаційні моделі відтворюють процеси, що протікають у реальній системі. У тому випадку, коли в моделі враховуються випадкові фактори, під час моделювання необхідно провести велику кількість прогонів моделі, як із різними вхідними даними, так і з різними послідовностями випадкових чисел. Для моделей детермінованих систем, у яких не враховуються випадкові фактори, зазвичай досить лише одного прогону моделі для всіх допустимих комбінацій вхідних даних і параметрів моделі. Однак на практиці такі моделі майже не зустрічаються.
У ході експерименту з моделлю одержують безліч даних, які мають бути структуровані та інтерпретовані для використання під час прийняття рішень стосовно структури та параметрів системи чи моделі. Для того щоб правильно інтерпретувати отримані вихідні дані, необхідно планувати проведення експериментів з моделлю. Планування експерименту — це розроблення такого плану експерименту, який дає можливість за мінімальної кількості прогонів моделі і за мінімальних затрат ресурсів зробити статистично значимі висновки або знайти оптимальні рішення щодо функціонування системи. Під час планування експериментів, як правило, визначають:
- вхідні дані для кожного експерименту і кількість прогонів імітаційної моделі;
- тривалість одного прогону моделі і перехідного процесу моделювання;
- стратегію збирання даних під час кожного прогону моделі;
- методи оцінювання точності вихідних даних і побудови довірчих інтервалів;
- чутливість моделі до вхідних даних, різних видів розподілів випадкових величин, сценаріїв поведінки модельованої системи;
- умови і сценарії проведення експерименту;
- умови генерування потоків випадкових чисел у системі моделювання та імовірнісних вхідних даних;
- стратегію досягнення мети експерименту (наприклад, порівняння альтернативних варіантів системи або оптимізація цільової функції).
Кінцева мета проведення експериментів – це одержання статистичної інформації, достатньої для прийняття рішень відповідно до результатів моделювання. Моделювання здебільшого провадиться з метою визначення деяких екстремальних значень характеристик модельованої системи (оптимізуючий експеримент) або для виявлення важливих факторів, які впливають на модельовану систему (відсіяний експеримент). Під час експериментів обох типів використовують факторні плани й будують поліноми різного порядку, які апроксимують поверхню відгуку. Для пошуку екстремальних значень застосовуються числові методи оптимізації. Під час таких експериментів визначається функціональна залежність вихідної змінної (функції відгуку, чи просто відгуку) від вхідних змінних, або факторів; ця залежність відображає критерій ефективності модельованої системи. Таким чином, пошук найкращого рішення характеризується числовим значенням цього критерію, і для знаходження екстремальних значень необхідно досліджувати по верхні відгуку (провадити експерименти) у різних точках факторного простору. Ефективність проведення експериментів багато в чому залежить від початкової точки у факторному просторі. Один із найважливіших видів експериментів, проваджуваних з моделлю, це структурна оптимізація [3], під якою будемо розуміти пошук найкращої структури модельованої системи. У цьому випадку аналізується кілька моделей, причому вони можуть відрізнятися структурою, параметрами і алгоритмами функціонування. Для таких експериментів не існує єдиного числового критерію оптимізації, що ускладнює використання класичних методів. Однак під час такого дослідження кількість моделей, як правило, невелика, тому для структурної оптимізації можна скористатися методом висування гіпотез або простим перебиранням варіантів. Оптимізація єдиного варіанта модельованої системи провадиться за допомогою пошуку вузьких місць і їх усунення, тобто балансування модельованої системи. Вузькі місця визначають пропускну здатність усієї системи, і пошук найкращого рішення здійснюється шляхом порівняння розглянутих варіантів. Перелічимо основні проблеми, які виникають під час проведення експериментів з імітаційними моделями.
1. Визначення початкових умов проведення експерименту.
Зазвичай експеримент починають, коли модель перебуває в стані «пусто і вільно», тобто в моделі немає динамічних об'єктів або транзактів і всі пристрої та ресурси вільні. Якщо розглядається досить тривалий період моделювання, то можна задати так званий період «розігріву» чи «розгону» моделі, або перехідний процес, після якого модель переходить у сталий (стаціонарний) режим роботи. Урахування даних перехідного процесу для оцінювання вихідних змінних моделі спричинює зміщення статистичних оцінок параметрів.
Щоб зменшити вплив вихідних даних перехідного процесу на кінцеві результати, моделювання слід починати з використання модальних (найбільш імовірних) або середніх значень сталого режиму. Такий спосіб запуску моделі забезпечує зменшення тривалості перехідного процесу моделі, але застосування даного способу ефективне лише в тому випадку, коли завантаження пристроїв обслуговування в моделі невелике. У разі наближення коефіцієнтів завантаження пристроїв до одиниці на виході моделі можна спостерігати стаціонарний процес, під час якого неможливо чітко визначити дані перехідного процесу (рис. 1).
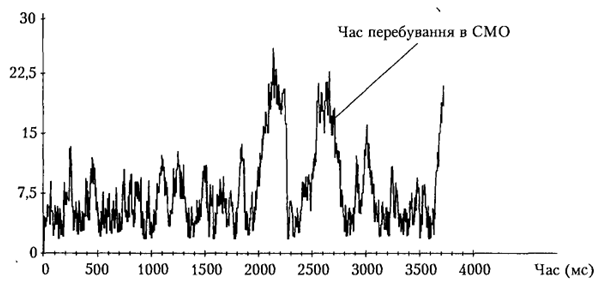
Рис. 1. Стаціонарний процес виходу із СМО з близьким до одиниці коефіцієнтом завантаження
У разі оцінювання статистичних параметрів вихідних величин рекомендується не враховувати дані перехідного процесу, оскільки вони можуть викликати істотне зміщення шуканих оцінок. Усунення зміщення досягається шляхом відкидання даних перехідного процесу (в мові GPSS це можна зробити, використавши команду RESET). Найскладнішим є встановлення моменту досягнення сталого стану системи. Досі не існує цілком надійних методів визначення цього моменту [4]. Однак дана проблема може бути вирішена за допомогою діалогових та інтелектуальних систем моделювання, які дають змогу контролювати і графічно відображати хід моделювання. Найефективніший спосіб визначення початку сталого режиму - це спостереження за графіками зміни вихідного процесу в часі (рис. 2).
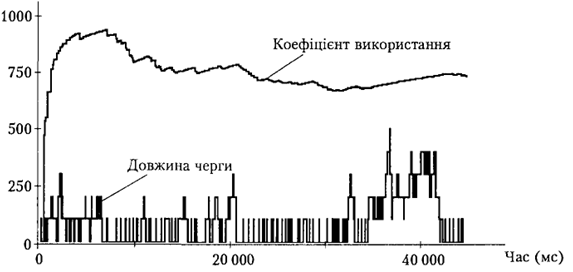
Рис. 2. Графіки вихідних даних моделі СМО
2. Зупинення процесу моделювання.
Правила зупинення процесу моделювання дозволяють визначити тривалість прогону імітаційної моделі — а від цього залежить точність результатів. Наприклад, якщо потрібно провести моделювання роботи виробничої дільниці протягом робочого тижня, то час прогону моделі можна визначити саме цим терміном. Дослідник сам приймає рішення, чи буде досягнуто за вказаний період моделювання сталий режим роботи моделі. Він також обирає метод збирання вихідних даних і оцінювання точності результатів моделювання. Точність оцінювання параметрів системи в цьому випадку визначається за одним досить тривалим прогоном моделі.
Визначають два типи імітаційного моделювання — скінченне і нескінченне. Для першого процес моделювання закінчується, коли відбувається «природна» подія, яка дає змогу визначити тривалість прогону моделі. Така подія часто відбувається в той момент, коли система звільняється від вимог, чи в момент, після якого вже не можна одержати корисної інформації, або моделювання закінчується за показниками таймера. Така подія визначається до виконання прогонів моделі, її настання має бути детермінованою (згідно з таймером) або випадковою величиною. Оскільки початкові умови скінченного моделювання, як правило, впливають на критерії оцінювання, вони мають представляти умови, характерні для роботи реальної системи.
Під час виконання нескінченного імітаційного моделювання не існує події, настання якої давало б змогу визначати тривалість прогону моделі. Моделювання цього типу використовується у разі дослідження поведінки системи за умов сталого режиму її роботи протягом тривалого часу. Параметри, що оцінюються в цьому випадку, вважаються сталими, якщо вони залежать від характеристик сталих законів розподілів ймовірностей деякого вихідного процесу.
3. Стан моделі в момент припинення прогону.
Під час моделювання завжди виникає питання щодо доцільності використання динамічних компонентів, або транзактів, які залишилися в моделі після закінчення її роботи. Урахування характеристик цих компонентів може призвести до збільшення зміщення статистичних оцінок параметрів моделі. На приклад, під час моделювання роботи дільниці цеху було зроблено припущення, що найменш тривалі роботи виконуються в першу чергу. Тоді на момент закінчення моделювання може виникнути ситуація, коли в моделі залишаться тільки роботи, термін виконання яких великий. Якщо їх не враховувати, оцінка середньої тривалості виконання робіт у цеху буде заниженою.
4. Визначення тривалості прогону моделі за наявності в ній процесів з різними швидкостями протікання.
Для оцінювання точності результатів моделювання здебільшого використовують параметри найповільнішого процесу в моделі. У цьому випадку оцінки для більш швидких процесів будуть набагато кращими і ефективнішими, ніж для повільних, тобто довірчі інтервали для останніх будуть більшими. Під час розроблення імітаційної моделі обирають такий ступінь її деталізації, щоб швидкості процесів, які протікають у моделі, не відрізнялися більш ніж на два порядки. У разі необхідності моделювання рідких подій або повільних процесів, наприклад відмов устаткування, потрібно укрупнювати стани для швидких процесів. Для цього використовують аналітико-імітаційні моделі.
Оцінювання точності результатів моделювання
Оцінити точність результатів моделювання можна шляхом побудови довірчих інтервалів для вихідних змінних (відгуків) моделі. Точність результатів залежить насамперед від кількості реалізацій (прогонів моделі) і тривалості прогону для кожної реалізації моделі. Якщо модель детермінована, то для отримання точних результатів моделювання достатньо одного прогону. У загальному випадку дані спостереження одного прогону моделі представляють одиничну вибірку або часовий ряд. Часовий ряд — це реалізація випадкового процесу. В результаті кожного прогону моделі утворюються часові ряди для кожного значення відгуку моделі досліджуваних випадкових процесів. Під час моделювання стохастичних систем потрібно розглядати два режими роботи моделей: перехідний і стаціонарний. Стаціонарний режим визначається сталим процесом на виході моделі. Слід зазначити, що для більшості реальних систем характеристики стохастичних процесів, у тому числі й закони розподілу, з часом змінюються. За наявності нової інформації відносно параметрів системи потрібно повторно проаналізувати сталі параметри моделі.
Перехідний режим роботи моделі
Для більшості виробничих систем неможливо гарантувати, що вони працюватимуть у стаціонарному режимі. Винятком є системи роботизованого автоматичного виробництва. Якщо модель працює в перехідному режимі, то необхідну кількість прогонів моделі можна розрахувати за тими ж формулам, що і для методу статистичних випробувань; при цьому під час кожного прогону моделі з використанням однакових вхідних даних і параметрів формується своя послідовність випадкових чисел. Оскільки випадкові величини незалежні, то незалежними мають бути й отримані вихідні дані для кожного прогону моделі. Це дає змогу побудувати довірчий інтервал, скориставшись центральною граничною теоремою. Необхідну точність ɛ можна задати, наприклад, такою, що дорівнює ± 5 % середнього значення величини, для якої будується довірчий інтервал, якщо а = 0,05. Після проведення прогонів моделі розраховуються оцінки загального середнього значення вихідної змінної та середньоквадратичного відхилення і будується довірчий інтервал для середнього значення. Більшість програмних засобів імітаційного моделювання забезпечують автоматичне проведення таких розрахунків. Наприклад, якщо модель реалізовано мовою GPSS World, то після останнього прогону достатньо викликати процедуру ANOVA, яка і побудує довірчі інтервали для вихідних змінних. Якщо кількість прогонів невелика (менше ніж 30), то для побудови довірчого інтервалу використовують розподіл Стьюдента (t-розподіл). За наявності більшого числа прогонів для визначення значення ta можна використовувати нормальний розподіл. Процедура повторних прогонів (реплікацій) має важливу властивість - незалежність вибірок. Ця властивість є універсальною і може застосовуватись для моделювання як перехідного, так і стаціонарного режиму роботи моделі. Слід зауважити, що в разі моделювання стаціонарного режиму ця процедура дає змогу зібрати дані й перехідного періоду, які не використовуються під час аналізу стаціонарного режиму.
Стаціонарний режим роботи моделі
Під час моделювання деяких систем, наприклад комп'ютерних та комунікаційних, виникає потреба аналізувати їх роботу в сталому, стаціонарному режимі. Існування такого режиму в системі дає змогу побудувати довірчий інтервал для оцінок параметрів за результатами не багатьох прогонів моделі, а лише одного, досить тривалого. Основна проблема, пов'язана з побудовою довірчого інтервалу, обумовлена тим, що вихідні дані імітаційної моделі є корельованими. Крім того, наявність перехідних процесів у моделі призводить до зміщення статистичних оцінок. На жаль, не існує надійних методів виявлення моменту завершення перехідного періоду роботи моделі. Якщо критерієм оцінювання є вартісна характеристика (прибуток, витрати та ін.), яка визначається для стаціонарного режиму роботи моделі, тривалість прогону може бути визначена на основі результатів спостереження за зміною величини, що дорівнює відношенню оцінюваного показника за весь період моделювання до тривалості моделювання (наприклад, витрати за одиницю часу), для якої будують графік зміни в модельному часі. Оскільки тривалість перехідного періоду може змінюватись в залежності від комбінацій вхідних змінних моделі і послідовностей випадкових чисел, потрібно визначити найдовший перехідний період. Статистичні дані перехідного періоду роботи моделі не повинні враховуватись під час розрахунків статистичних оцінок для вихідних змінних. Необхідно, щоб тривалість прогону відповідала сталому режиму функціонування моделі (рис. 3). На практиці діють таким чином. За графіком вихідної змінної моделі визначають час моделювання, коли закінчується перехідний період tпер. Статистичні дані, зібрані за цей період, не враховуються під час стати стичного аналізу. Наприклад, у мові GPSS це робиться за допомогою команди RESET, яка видаляє накопичені статистичні дані, але залишає транзакти в моделі, фіксує поточні значення довжин черг і максимальний вміст блоків STORAGE. Після цього повторно викликається команда START, що задає тривалість прогону моделі не меншою ніж 100tпер.
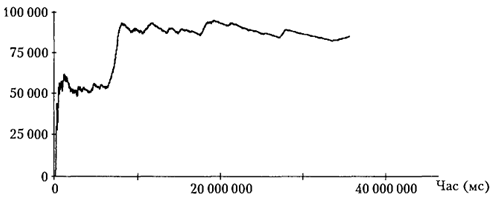
Рис. 3. Визначення сталого режиму роботи моделі
Розглянутий вище спосіб є наближеним, але він широко використовується на практиці. Існують інші методи, застосування яких дає змогу отримати більш надійні оцінки для характеристик стаціонарних процесів. У книзі А. Лоу і В. Келтона [2] описується шість методів для обчислення оцінки стаціонарного середнього випадкового процесу, серед яких основну увагу приділено методу реплікації і вилучення.
Особливості планування експериментів
Послідовність дій, які необхідно виконувати під час планування експериментів.
- Визначення відгуків (вихідних змінних) системи.
- Визначення факторів, які впливають на відгук системи. Більшість систем підпорядковуються принципу Парето - з огляду на характеристики системи істотними є лише деякі з множини факторів. У більшості систем 20 % факторів визначають 80 % властивостей системи.
- Визначення рівнів факторів. Мінімальна кількість рівнів для кожного фактора два - нижня і верхня межі значення фактора. У разі використання цього числа рівнів можна визначити тільки лінійні ефекти. Для врахування квадратичних ефектів необхідно використовувати три рівні, для кубічних ефектів – чотири і т. д. Аналіз значно спрощується, якщо брати тільки рівновіддалені одне від одного значення рівнів. У цьому випадку маємо так зване ортогональне планування, або ортогональний експеримент.
Для множинних експериментів з числом факторів більше одного дисперсійний аналіз передбачає використання для заключного аналізу ортогонального експерименту. Це означає, що оцінки відгуків у межах аналізу мають бути некорельованими. На практиці ортогональність гарантує використання тих самих випадкових послідовностей чисел під час виконання експериментів у межах кожної комбінації рівнів обробки.