Відмінності між версіями «Насадка Борда»
| Рядок 10: | Рядок 10: | ||
| − | <math>Q={{\mu }_{}}\omega \sqrt{2g{{H}_{c}}}</math> (1) | + | '''<math>Q={{\mu }_{}}\omega \sqrt{2g{{H}_{c}}}</math>''' (1) |
де <math>{{H}_{c}}</math> - напір на рівні центру тяжіння отвору | де <math>{{H}_{c}}</math> - напір на рівні центру тяжіння отвору | ||
| Рядок 24: | Рядок 24: | ||
| − | <math>{{Z}_{1}}+\frac{P1}{\rho g}+\frac{a1\nu _{1}^{2}}{2g}={{Z}_{2+}}\frac{P2}{\rho g}+\frac{a2\nu _{2}^{2}}{2g}+{{k}_{\omega 1-2}}</math> (2) | + | '''<math>{{Z}_{1}}+\frac{P1}{\rho g}+\frac{a1\nu _{1}^{2}}{2g}={{Z}_{2+}}\frac{P2}{\rho g}+\frac{a2\nu _{2}^{2}}{2g}+{{k}_{\omega 1-2}}</math>''' (2) |
| Рядок 38: | Рядок 38: | ||
| − | <math>hw=hr={{\xi }_{}}\frac{\nu _{c}^{2}}{2g}</math> | + | '''<math>hw=hr={{\xi }_{}}\frac{\nu _{c}^{2}}{2g}</math>''' |
Після підстановки значень визначається величина швидкості витікання через отвір при наявності насадка: | Після підстановки значень визначається величина швидкості витікання через отвір при наявності насадка: | ||
| − | + | ||
| − | <math>{{H}_{1}}+\frac{{{P}_{a}}}{\rho g}=\frac{{{P}_{a}}}{\rho g}-\frac{\rho g{{h}_{}}}{\rho g}+\frac{a\nu _{c}^{2}}{2g}+{{\xi }_{}}\frac{\nu _{c}^{2}}{2g}</math> | + | '''<math>{{H}_{1}}+\frac{{{P}_{a}}}{\rho g}=\frac{{{P}_{a}}}{\rho g}-\frac{\rho g{{h}_{}}}{\rho g}+\frac{a\nu _{c}^{2}}{2g}+{{\xi }_{}}\frac{\nu _{c}^{2}}{2g}</math>''' |
| − | |||
Версія за 20:55, 5 червня 2011
Насадка Борда-(Насадка внутрішня) (рос. насадка внутренняя (Борда); англ. internal mouthpiece (Borda); нім. Inneneinsatz m, Borda-Inneneinsatz m, Innenaufsatz m) – круглоциліндрична насадка, розміщена з внутрішнього боку стінки посудини (або водойми), з якої вона живиться. Насадка Борда використовується для спорожнення резервуарів, коли з конструктивних міркувань не можна встановити насадок Вентурі .
Історія винекнення
Внутрішня насадка Борда названа на честь французького вченого, фізика та геодезиста Шарля Жан Борда (4.5.1733, Дакс, — 19.2.1799, Париж)Член Паризької АН. Служив офіцером у армії, потім на флоті. Визначив (1792) довжину секундного маятника в Парижі і знайшов спосіб точного визначення періоду хитання маятника. 1766р. запропонував внутрішню насадку для збільшення витрати рідини, яка витікає з судини, при заданому перерізі вихідного отвору. Довів що носить його ім'я теорему в гідравліці про удар струменя рідини чи газу. Розробив одну із систем вертикальних осей астрономо-геодезичних інструментів.
Витікання рідини через внутрішню насадку
[math]Q={{\mu }_{}}\omega \sqrt{2g{{H}_{c}}}[/math] (1)
де [math]{{H}_{c}}[/math] - напір на рівні центру тяжіння отвору [math]{{\mu }_{}}[/math] - коефіцієнт витрат великого отвору
Формула (1) і значення [math]{{\mu }_{}}[/math] можуть бути застосовані для отворів будь-якої форми.
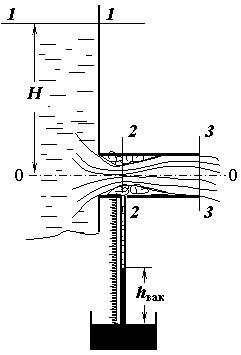
Приєднання насадка до отвору того ж діаметру змінює характер перебігу. Це добре можна показати, застосовуючи рівняння Бернуллі до січень 1-1 і 2-2, а потім 1-1 і 3-3.Як можна бачити на (рис.1), потік рідини в насадці можна розділити на дві зони. Основна частина - це власне струмінь. Течія в області стиснутого перерізу (2-2), несталий. Воно виникає внаслідок того, що при видаленні повітря з цієї області на початку руху, тут утворюється зона розрідження. Величину вакууму легко вимірюють за допомогою вакуумметра будь-якої конструкції. Наявність вакууму всередині насадка, приєднаного до отвору, сприяє додатковому підсосу рідини і збільшення пропускної здатності отвори, що визначається за рівнянням Бернуллі для перерізів 1-1 і 2-2.
[math]{{Z}_{1}}+\frac{P1}{\rho g}+\frac{a1\nu _{1}^{2}}{2g}={{Z}_{2+}}\frac{P2}{\rho g}+\frac{a2\nu _{2}^{2}}{2g}+{{k}_{\omega 1-2}}[/math] (2)
z1=H
p1=pa
[math]\rho[/math]=0
z2=0
p2=pa-[math]\rho[/math]ghвак
[math]hw=hr={{\xi }_{}}\frac{\nu _{c}^{2}}{2g}[/math]
Після підстановки значень визначається величина швидкості витікання через отвір при наявності насадка:
[math]{{H}_{1}}+\frac{{{P}_{a}}}{\rho g}=\frac{{{P}_{a}}}{\rho g}-\frac{\rho g{{h}_{}}}{\rho g}+\frac{a\nu _{c}^{2}}{2g}+{{\xi }_{}}\frac{\nu _{c}^{2}}{2g}[/math]