Відмінності між версіями «Рівняння нерозривності»
(→Література) |
|||
| Рядок 8: | Рядок 8: | ||
<math>p\cdot V\cdot dx\cdot dy</math> - маса рідини, яка витікає з грань <math>\textbf{\textit{xz}}</math>. <br><br> | <math>p\cdot V\cdot dx\cdot dy</math> - маса рідини, яка витікає з грань <math>\textbf{\textit{xz}}</math>. <br><br> | ||
<math>[pV+dy\cdot \frac{\partial(pV)}{dy}]dx\cdot dz</math> - маса рідини, яка витікає з <math>\textbf{\textit{xz}}</math>: <br><br><math>\frac{\partial(pV)}{dy}</math> - приріст <math>\textbf{\textit{pV}}</math><br><br> | <math>[pV+dy\cdot \frac{\partial(pV)}{dy}]dx\cdot dz</math> - маса рідини, яка витікає з <math>\textbf{\textit{xz}}</math>: <br><br><math>\frac{\partial(pV)}{dy}</math> - приріст <math>\textbf{\textit{pV}}</math><br><br> | ||
| + | |||
| + | ==Загальний вигляд== | ||
Вздовж осі <math>\textbf{\textit{Oy}}</math> маса рідини змінилася на величину:<br><br> | Вздовж осі <math>\textbf{\textit{Oy}}</math> маса рідини змінилася на величину:<br><br> | ||
| Рядок 16: | Рядок 18: | ||
З іншого боку, приріст маси може отриматись за рахунок змінної густини<br><br> | З іншого боку, приріст маси може отриматись за рахунок змінної густини<br><br> | ||
<math>dm=-\frac{\partial p}{\partial t}dx\cdot dy\cdot dz</math><br><br> | <math>dm=-\frac{\partial p}{\partial t}dx\cdot dy\cdot dz</math><br><br> | ||
| + | |||
| + | ==Кінцева формула== | ||
| + | |||
Отже, можна отримати рівняння нерозривності у одному з виглядів<br><br> | Отже, можна отримати рівняння нерозривності у одному з виглядів<br><br> | ||
<math>\frac{\partial(pU)}{dx}+\frac{\partial(pV)}{dy}+\frac{\partial(pW)}{dz}=-\frac{\partial p}{\partial t}</math><br><br> | <math>\frac{\partial(pU)}{dx}+\frac{\partial(pV)}{dy}+\frac{\partial(pW)}{dz}=-\frac{\partial p}{\partial t}</math><br><br> | ||
Версія за 21:02, 8 травня 2011
В гідрогазодинаміці в багатьох випадках можна знехтувати стисливістю рідин і газів. Тому використовують єдиний підхід до вивчення їх поведінки, користуючись єдиним поняттям нестисливої рідини - суцільного середовища з однаковою в усіх точках густиною, яка не змінюється з часом. Це своєрідна модель ідеальної рідини, в якій не враховується наявне в рідині внутрішне тертя.
Спираючись на закон збереження маси, отримаємо рівняння нерозривності, яке замикає систему рівнянь Ейлера.
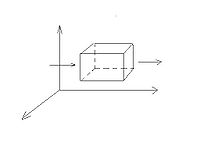
Припустимо, що рідина рухається без виникнення пустот. Виділимо елементарний об’єм.
[math]p\cdot V\cdot dx\cdot dy[/math] - маса рідини, яка витікає з грань [math]\textbf{\textit{xz}}[/math].
[math][pV+dy\cdot \frac{\partial(pV)}{dy}]dx\cdot dz[/math] - маса рідини, яка витікає з [math]\textbf{\textit{xz}}[/math]:
[math]\frac{\partial(pV)}{dy}[/math] - приріст [math]\textbf{\textit{pV}}[/math]
Загальний вигляд
Вздовж осі [math]\textbf{\textit{Oy}}[/math] маса рідини змінилася на величину:
[math]\begin{cases} \frac{\partial(pV)}{dy}dx\cdot dy\cdot dz\\ \frac{\partial(pW)}{dz}dx\cdot dy\cdot dz\\ \frac{\partial(pU)}{dx}dx\cdot dy\cdot dz\end{cases}[/math]
Приріст маси:
[math][\frac{\partial(pU)}{dx}+\frac{\partial(pV)}{dy}+\frac{\partial(pW)}{dz}]dx\cdot dy\cdot dz[/math]
З іншого боку, приріст маси може отриматись за рахунок змінної густини
[math]dm=-\frac{\partial p}{\partial t}dx\cdot dy\cdot dz[/math]
Кінцева формула
Отже, можна отримати рівняння нерозривності у одному з виглядів
[math]\frac{\partial(pU)}{dx}+\frac{\partial(pV)}{dy}+\frac{\partial(pW)}{dz}=-\frac{\partial p}{\partial t}[/math]
[math]\frac{\partial p}{\partial t}+div\quad p\overrightarrow{V}=0[/math]
за умови, що [math]p\neq const[/math].
Припустимо [math]p=const[/math], тоді рівняння нерозривності
[math]div \vec{V}=0[/math]
[math]\frac{\partial U}{\partial x}+\frac{\partial V}{\partial y}+\frac{\partial W}{\partial z}=0[/math]
Це рівняння доповнює систему рівнянь Ейлера до замкнутої системи чотирьох рівнянь відносно чотирьох невідомих функцій.
Література
Милн-Томсон Л. М. «Теоретическая гидродинамика». пер. з англ., М., 1964.