|
|
| Рядок 1: |
Рядок 1: |
| − | == Закон Бернуллі ==
| + | '''Рівня́ння Берну́ллі''' ({{lang-ru|уравнение Бернулли}}; {{lang-en|Bernoulli's theorem}}; {{lang-de|Bernulligleichung}}) — рівняння гідроаеромеханіки, яке визначає зв'язок між швидкістю '''v''' [[рідина|рідини]], [[тиск]]ом '''p''' в ній та висотою '''h''' частинок над площиною відліку. |
| − | Інтегра́л Берну́ллі рівнянь гідродинаміки — це інтеграл, що визначає в кожній точці потоку ідеальної рідини або баротропного газу тиск <math>p</math>, що встановився: (<math>p=F(\rho)</math>) через швидкість <math> \vec v</math> потоку у відповідній точці та через силову функцію <math> \vec u(x,y,z)</math> об'ємних сил:<br />
| + | {{приєднати|Інтеграл Бернуллі}} |
| − | <math>\int \frac{dp}{\rho}\ = C - \frac{1}{2}\left | \vec v^2 \right | + \vec u</math> <br />
| + | Встановив його у [[1738]] р. [[Бернуллі Даніель|Д. Бернуллі]]. |
| − | Стала <math>C</math> має для кожної лінії струменю своє значення, що змінюється з переходом від одної лінії струменю до іншої. Якщо рух потенційний, то стала <math>C</math> одна і таж для всього потоку.<br />
| |
| − | Для руху, що не встановився, інтеграл Бернулі (називають інколи ''інтегралом Коші—Лагранжа'') має місце за наявності потенціалу швидкостей:<br />
| |
| − | <math>\int \frac{dp}{\rho}\ = \frac{\partial \phi}{ \partial t} - \frac{1}{2}\left | \vec v^2 \right | + \vec u + f(t)</math>, <br />
| |
| − | причому <math> \mathbf{v} = \text{grad}\, \phi(x,y,z,t)</math> а <math>f(t)</math> — довільна функція часу.<br />
| |
| − | Для нестискуваних рідин ліва частина рівнянь приводиться до вигляду <math>\frac{p}{\rho}</math> для баротропного газу (<math>p=F(\rho)</math>) — до вигляду:<br />
| |
| − | <math>\int \frac{dp}{\rho}\ = \int F'(\rho) \frac{d \rho}{\rho}\ </math> <br />
| |
| − | Інтеграл Бернулі запропоновано Бернуллі Даніель ( <u>1738</u>)
| |
| | | | |
| | + | Для [[ламінарна течія|ламінарної]] течії [[ідеальна рідина|ідеальної]] (нестисненої) рідини рівняння Бернуллі має вигляд: |
| | + | :<math>h+\frac{v^{2}}{2g}+\frac{p}{\rho g}=\text{const}</math> |
| | | | |
| − | '''Закон Бернулли''' является следствием [[закон сохранения энергии|закона сохранения энергии]] для стационарного потока [[идеальная жидкость|идеальной]] (то есть без внутреннего трения) несжимаемой жидкости:
| + | або<br /> |
| − | : <math>\tfrac{\rho v^2}{2} + \rho g h + p = \mathrm{const}</math> | + | :<math>h\rho g+p+\frac{\rho v^{2}}{2}=\text{const}</math>, |
| − | Здесь
| |
| − | : <math>~\rho</math> — [[плотность]] жидкости,
| |
| − | : <math>~v</math> — [[скорость]] потока,
| |
| − | : <math>~h</math> — [[высота]], на которой находится рассматриваемый элемент жидкости,
| |
| − | : <math>~p</math> — [[давление]] в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
| |
| − | : <math>~g</math> — [[ускорение свободного падения]].
| |
| | | | |
| − | Константа в правой части обычно называется ''напором'', или полным давлением, а также '''интегралом Бернулли'''. Размерность всех слагаемых — единица энергии, приходящейся на единицу объёма жидкости.
| + | де ρ — [[густина]] рідини; g — [[прискорення вільного падіння]]. |
| | | | |
| − | Это соотношение, выведенное [[Даниил Бернулли|Даниилом Бернулли]] в [[1738 год в науке|1738]] г., было названо в его честь ''уравнением Бернулли''. (Не путать с [[Дифференциальное уравнение Бернулли|дифференциальным уравнением Бернулли]].)
| + | В останньому рівнянні всі члени мають розмірність [[тиск]]у, p — [[статичний тиск]]; <math>\frac{\rho v^{2}}{2}</math> — [[динамічний тиск]]; hρg — ваговий тиск. |
| | + | [[Файл:BernoullisLawDerivationDiagram.png|thumb|400px]] |
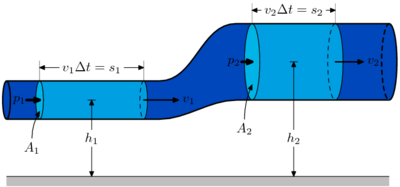
| | + | Якщо такі рівняння записати для двох перерізів течії, то матимемо: |
| | + | :<math>\frac{v_{1}^{2}}{2}+g h_{1}+\frac{p_{1}}{\rho}=\frac{v_{2}^{2}}{2}+g h_{2}+\frac{p_{2}}{\rho}</math> |
| | | | |
| − | Для горизонтальной трубы <math>h=0</math> и уравнение Бернулли принимает вид: <math>\tfrac{\rho v^2}{2}+p=\mathrm{const}</math>. | + | Для горизонтальної течії середні члени у лівій і правій частині рівняння скорочуються і воно набуває вигляду: |
| | + | :<math>\frac{v_{1}^{2}}{2}+\frac{p_{1}}{\rho}=\frac{v_{2}^{2}}{2}+\frac{p_{2}}{\rho}</math> |
| | | | |
| − | Эта форма уравнения Бернулли может быть получена путём интегрирования [[Уравнение Эйлера|уравнения Эйлера]] для стационарного одномерного потока жидкости, при постоянной плотности <big><math>\rho</math></big>: <math>v\tfrac{dv}{dx}=-\tfrac {1}{\rho}\cdot \tfrac {dp}{dx}</math>.
| + | тобто в усталеній горизонтальній течії ідеальної нестисненої рідини в кожному її перерізі сума статичного і динамічного тисків буде сталою. Отже, в тих місцях течії, де швидкість рідини більша (вузькі перерізи), її динамічний тиск збільшується, а статичний зменшується. На цьому явищі заснована дія струминних насосів, ежекторів, витратомірів Вентурі і Піко, [[пульверизатор]]ів. |
| | | | |
| − | [[Файл:BernoullisLawDerivationDiagram.png |thumb|400px|right]] | + | Рівняння Бернуллі є наслідком [[закон збереження енергії|закону збереження енергії]]. Якщо рідина не ідеальна, то її [[механічна енергія]] розсіюється і тиск вздовж трубопроводу, яким тече така рідина, спадає. Для реальної в'язкої рідини в правій частині рівнянь, слід додати величину втрат тиску '''Δр<sub>вт</sub>''' на гідравлічний опір рухові. |
| | | | |
| − | Согласно закону Бернулли полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.
| + | Рівняння Бернуллі широко застосовують для розв'язання багатьох гідравлічних задач у нафтогазовій справі. |
| − | | |
| − | '''Полное давление''' состоит из весового <math>(\rho g h)</math>, статического <math>(p)</math> и динамического <math>\left(\tfrac{\rho v^2}{2}\right)</math> давлений.
| |
| − | | |
| − | Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной [[Эффект Магнуса|эффекта Магнуса]]. Закон Бернулли справедлив и для [[Ламинарное течение|ламинарных]] потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода [[расходомер]]ов (например [[труба Вентури]]), водо- и пароструйных [[насос]]ов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — [[Гидравлика|гидравлики]].
| |
| − | | |
| − | Закон Бернулли справедлив в чистом виде только для жидкостей, [[вязкость]] которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы. На самом деле экспериментально установлено, что скорость жидкости на поверхности твердого тела почти всегда в точности равна нулю (кроме случаев отрыва струй при некоторых редких условиях).
| |
| − | | |
| − | == Одно из применений ==
| |
| − | Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда.
| |
| − | | |
| − | [[Файл:ЭФФЕКТ_ВЕНТУРИ.GIF|thumb|Закон Бернулли позволяет объяснить эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше чем на участке трубы большего диаметра, в результате чего наблюдается разница высот столбов жидкости <math>\Delta h</math>; бо́льшая часть этого перепада давлений обусловлена изменением скорости течения жидкости, и может быть вычислена по уравнению Бернулли]]
| |
| − | | |
| − | Согласно закону Бернулли приравняем полные давления на верхней поверхности жидкости и на выходе из отверстия:
| |
| − | : <math>\rho g h + p_0 = \frac{\rho v^2}{2} + p_0</math>,
| |
| − | где
| |
| − | : <math>p_0</math> — [[атмосферное давление]],
| |
| − | : <math>h</math> — высота столба жидкости в сосуде,
| |
| − | : <math>v</math> — скорость истечения жидкости,
| |
| − | : <math>z\, +\, \frac{p}{\rho g}</math> — гидростатический напор (сумма геометрического напора ''z'' и пьезометрической высоты <math> \frac{p}{\rho g}</math>).
| |
| − | | |
| − | Отсюда: <math>v = \sqrt{2gh}</math>. Это — формула [[Торричелли]]. Она показывает, что при истечении идеальной несжимаемой жидкости из отверстия в широком сосуде жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты <math>h</math>.
| |
| − | | |
| − | Часто уравнение Бернулли записывается в виде:
| |
| − | | |
| − | : <math>Hd\, =\, z\, +\, \frac{p}{\rho g}\, +\, \frac{v^2}{2\,g}=\, \text{const}\,</math>
| |
| − | | |
| − | где
| |
| − | : <math>Hd\,</math> — гидродинамический напор,
| |
| − | :: <math> \frac{v^2}{2\,g}</math> — скоростной напор.
| |
| − | | |
| − | == Для сжимаемого идеального газа ==
| |
| − | | |
| − | | |
| − | : <math>\frac {v^2}{2}+ gh+\left(\frac {\gamma}{\gamma-1}\right)\frac {p}{\rho} = \mathrm{const}</math><ref>Clancy, L.J., ''Aerodynamics'', Section 3.11</ref> (постоянна вдоль линии тока или линии вихря)
| |
| − | | |
| − | где
| |
| − | : <math>\gamma = \frac{C_p}{C_V}</math> — [[Показатель адиабаты|Адиабатическая постоянная]] газа
| |
| − | : <math>p</math> — [[давление]] газа в точке
| |
| − | : <math>\rho</math> — плотность газа в точке
| |
| − | : <math>v</math> — скорость течения газа
| |
| − | : <math>g</math> — [[ускорение свободного падения]]
| |
| − | : <math>h</math> — высота относительно начала координат
| |
| − | | |
| − | При движении в неоднородном поле <math>gh</math> заменяется на [[потенциал]] гравитационного поля.
| |
| − | | |
| − | == Термодинамика закона Бернулли ==
| |
| − | Из [[Статистическая физика|статистической физики]] следует, что на линиях тока при адиабатическом течении остается постоянным следующее соотношение:
| |
| − | : <math> \frac{v^2}{2} + w + \varphi = \mathrm{const} </math>
| |
| − | где <math> w </math> — [[энтальпия]] единицы массы, <math> \varphi</math> — потенциал силы.
| |
| − | {{Hider|
| |
| − | title = Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений |
| |
| − | hidden =1 |
| |
| − | content =
| |
| − | 1. Запишем [[Уравнение Эйлера]]:
| |
| − | : <math> \rho \frac{\partial \vec v}{\partial t} + \rho (\vec v, \nabla) \vec v = - \nabla p - \rho \nabla \varphi </math>
| |
| − | :: <math> \varphi </math> — потенциал. Для силы тяжести <math> \varphi = gz </math>
| |
| − | 2. Запишем выражение для [[Энтальпия|энтальпии]] и предположим, что [[энтропия]] системы постоянна (или, можно сказать, что [[Адиабатический процесс|течение адиабатично]]):
| |
| − | : <math> dW = V dP + T dS</math>
| |
| − | Пусть <math> S=const</math> и <math> w </math> — энтальпия единицы массы, тогда:
| |
| − | : <math> dw = \frac{dp}{\rho}</math>
| |
| − | или
| |
| − | : <math> \nabla w = \frac{\nabla p}{\rho}</math>
| |
| − | 3. Воспользуемся следующими соотношениями из [[Векторная алгебра|векторной алгебры]]:
| |
| − | : <math> \frac 12 \nabla v^2 = (\vec v, \nabla) \vec v + \vec v \times \operatorname{rot}\vec v </math>
| |
| − | : <math> \vec l \cdot \nabla = \frac{\partial}{\partial l}</math> — проекция градиента на некоторое направление равно производной по этому направлению.
| |
| − | 4. Уравнение Эйлера с использованием соотношений выведенных выше:
| |
| − | : <math> \rho \frac{\partial \vec v}{\partial t} + \rho \left[ \frac 12 \nabla v^2 - \vec v \times \operatorname{rot}\vec v \right] = - \rho \nabla (\varphi + w) </math>
| |
| − | Спроецируем это уравнение на единичный вектор касательный к [[Линия тока|линии тока]], учитывая следующее:
| |
| − | :: <math> \frac{\partial \vec v}{\partial t} = 0 </math> — условие стационарности
| |
| − | :: <math> (\vec l , \vec v \times \operatorname{rot}\vec v ) = 0 </math> — так как <math> \vec l ||\vec v </math>
| |
| − | Получаем:
| |
| − | : <math> \frac{\partial}{\partial l} \left( \frac{v^2}{2} + w + \varphi \right) = 0 </math>
| |
| − | То есть на линиях тока в стационарной адиабатической жидкости выполняется следующее соотношение:
| |
| − | : <math> \frac{v^2}{2} + w + \varphi = \operatorname{const} </math>
| |
| − | |
| |
| − | title-style = color: black; font-weight: bold; text-align: left;|
| |
| − | content-style = color: black; text-align: left; |
| |
| − | }}
| |
| − | | |
| − | == Практические следствия ==
| |
| − | * закон Бернулли объясняет эффект притяжения между телами, находящимися на границе потока движущейся жидкости (газа). Иногда это притяжение может создавать угрозу безопасности. Например, при движении [[Электропоезд «Сапсан»|скоростного поезда «Сапсан»]] (скорость движения более 200 км/час) для людей на платформах возникает опасность сброса под поезд<ref>[http://www.bbc.co.uk/russian/russia/2010/03/100326_sapsan_stones.shtml Би-Би-Си: «Камни для „Сапсана“, или „месть бедных“»]</ref>. Аналогично «затягивающая сила» возникает при движении судов параллельным курсом: например, подобные инциденты происходили с лайнером «[[Олимпик (лайнер)#Вторая неудача — инцидент с крейсером «Хоук»|Олимпик]]».
| |
| − | | |
| − | == Приложение ==
| |
| − | {{Hider|
| |
| − | title = Вывод уравнения Бернулли |
| |
| − | hidden =1 |
| |
| − | content =
| |
| − | : Энергия маленького элемента жидкости: <math>E=\frac{mv^2}2+U</math> (U - потенциальная энергия)
| |
| − | : Слева на большой объем жидкости между двумя поверхностями действует сила <math>p_1\cdot S_1</math>, а справа - <math>-p_2\cdot S_2</math> (минус, потому что влево).
| |
| − | : Итак, этот объем жидкости сдвинулся (за время <math>dt</math>). Пусть его левая граница сдвинулась на <math>dl_1</math>, а правая - на <math>dl_2</math>.
| |
| − | : Пишем условие несжимаемости: <math>S_1\cdot dl_1=V_1=V_2=S_2\cdot dl_2</math>. Объёмы, как видно, бесконечно малые, дифференциальные. Их самих можно рассматривать как дифференциалы объёма всего большого элемента.
| |
| − | : Далее. Сначала наш большой элемент состоял из левого голубого элемента и средней синей части. Теперь он состоит из средней синей части и правого голубого элемента. При этом все его молекулы сдвинулись, но так как течение стационарное, то в каждой точке со временем энергия не меняется. Поэтому энергия средней синей части не поменялась. Поэтому работа сил (ну, или за бесконечно малое время не сама работа, а её дифференциал) равна изменению энергии, равному, в свою очередь, энергии правого голубого элементика (который добавился) минус энергия левого голубого элементика (который, наоборот, ушёл, влился в средний синий). <math>p_1\cdot S_1\cdot dl_1 - p_2\cdot S_2\cdot dl_2 = dA = E_2-E_1 = \frac{m_2\cdot v_2^2}2+U_2-\frac{m_1\cdot v_1^2}2-U_1 = \frac{\rho V_2v_2^2}2+U_2-\frac{\rho V_1v_1^2}2-U_1</math>.
| |
| − | : Теперь вспоминаем формулу несжимаемости и сокращаем на объём. <math>p_1-p_2 = \frac{\rho v_2^2}2-\frac{\rho v_1^2}2+{U_2\over V_2}-{U_1\over V_1}</math>.
| |
| − | : Сгруппируя слагаемые, получаем формулу Бернулли: <math>p_1+{U_1\over V_1}+\frac{\rho v_1^2}2 = p_2+{U_2\over V_2}+\frac{\rho v_2^2}2</math>, или просто <math>p+\frac UV+\frac{\rho v^2}2=const</math>, или, подставив потенциальную энергию, <math>p+\rho gh+\frac{\rho v^2}2=const</math>.
| |
| − | |
| |
| − | title-style = color: black; font-weight: bold; text-align: left;|
| |
| − | content-style = color: black; text-align: left; |
| |
| − | }}
| |
| − | | |
| − | | |
| − | | |
| − | == Литература ==
| |
| − | * {{Книга:Ландау Л.Д., Лифшиц Е.М.: Гидродинамика|2003}}
| |
| − | | |
| − | | |
| − | | |
| − | | |
| − | == Література ==
| |
| − | | |
| − | ''Милн-Томсон Л. М.'' «Теоретическая гидродинамика». пер. з англ., М., 1964
| |
| − | | |
| − | [[Категорія:гідродинаміка]]
| |