Відмінності між версіями «Нейронні мережі»
Symchak (обговорення • внесок) |
Symchak (обговорення • внесок) |
||
| Рядок 51: | Рядок 51: | ||
*монотонність і диференційованість на всій осі абсцис; | *монотонність і диференційованість на всій осі абсцис; | ||
*простий вираз для похідної, що дає можливість використовувати широкий спектр оптимізаційних алгоритмів. | *простий вираз для похідної, що дає можливість використовувати широкий спектр оптимізаційних алгоритмів. | ||
| + | |||
| + | |||
| + | |||
| + | == Персептрон == | ||
| + | Перші персептрони були створені Ф.Розенблатом у 60-х роках і викликали великий інтерес. [[Файл:Perceptron.png|right|thumb|350px|Персептрон]]Первинна ейфорія змінилася розчаруванням, коли виявилося, що персептрони не здатні навчитися рішенню ряду простих задач. М.Мінський строго проаналізував цю проблему і показав, що є жорсткі обмеження на те, що можуть виконувати одношарові персептрони, і, отже, на те, чому вони можуть навчатися. Оскільки у той час методи навчання багатошарових мереж не були відомі, дослідники перейшли в більш багатообіцяючі області, і дослідження у області нейронних мереж прийшли в занепад. Відкриття методів навчання багатошарових мереж більшою мірою, ніж який-небудь інший чинник, вплинуло на відродження інтересу і дослідницьких зусиль. | ||
| + | Навчання персептрона: | ||
| + | *Ініціалізація вагових матриць W (випадкові значення) | ||
| + | *Подати вхід X і обчислити вихід Y для цільового вектора YT | ||
| + | *Якщо вихід правильний – перейти на крок 4; інакше обчислити різницю D = YT – Y; модифікувати ваги за формулою: | ||
| + | <br>wij(e+1) = wij(e) + α D Хі, | ||
| + | <br>де wij(e) – значення ваги від нейрона i до нейрона j до налагодження, wij(e+1) – значення ваги після налагодження, α – коефіцієнт швидкості навчання, Хi – вхід нейрона i, e – номер епохи (ітерації під час навчання). | ||
| + | *Виконувати цикл з кроку 2, поки мережа не перестане помилятися. На другому кроці у випадковому порядку пред’являються всі вхідні вектори. | ||
| + | |||
| + | <br>Один з найпесимістичніших результатів Мінського показує, що одношаровий персептрон не може відтворити таку просту функцію, як ВИКЛЮЧАЄ АБО. Це функція від двох аргументів, кожний з яких може бути нулем або одиницею. Вона приймає значення одиниці, коли один з аргументів рівний одиниці (але не обидва). | ||
| + | |||
== Список використаних джерел == | == Список використаних джерел == | ||
Версія за 11:07, 24 лютого 2011
| Презентація доповіді на тему Нейронні мережі. Реалізація в MatLab. є розміщеною в Репозиторії. |
| {{{img}}} | ||
| Імя | Володимир | |
| Прізвище | Симчак | |
| По-батькові | Сергійович | |
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | СН-10-097 | |
Зміст
Біологічні нейронні мережі
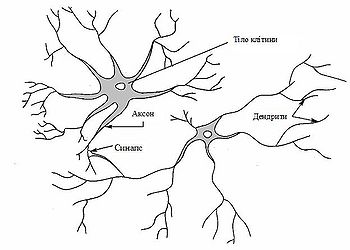
Нервова система людини побудована з елементів (нейронів), має приголомшуючу складність. Близько 1011 нейронів беруть участь в приблизно 1015 передаючих зв'язках, що мають довжину метр і більше. Кожен нейрон володіє багатьма якостями, спільними з іншими елементами тіла, але його унікальною здатністю є прийом, обробка і передача електрохімічних сигналів по нервових шляхах, які утворюють комунікаційну систему мозку.Дендрити (входи нейрона) йдуть від тіла нервової клітини до інших нейронів, де вони приймають сигнали в точках з'єднання (синапсах). Прийняті синапсом вхідні сигнали підводяться до тіла нейрона. Тут вони підсумовуються, причому одні входи стимулюють активізацію нейрона, а інші – зниження його активності. Коли сумарна активність (збудження) нейрона перевищує деякий поріг, нейрон переходить в активний стан, посилаючи по аксону (виходу нейрона) сигнал іншим нейронам. У цієї основної функціональної схеми багато спрощень і виключень, проте більшість штучних нейронних мереж моделює лише ці прості властивості.
Історія розвитку штучних нейронних мереж
1943 рік — Норберт Вінер разом з співробітниками публікує роботу про кібернетику. Основною ідеєю є представлення складних біологічних процесів математичними моделями.
1943 рік — Маккалок та Піттс формалізують поняття нейронної мережі у фундаментальній статті про логічне числення ідей і нервової активності.
1949 рік — Хебб пропонує перший алгоритм навчання.
У 1958 році Розенблаттом винайдений перцептрон. Перцептрон набуває популярності — його використовують для розпізнавання образів, прогнозування погоди і т. д.
У 1960 році Уідроу спільно зі своїм студентом Хоффом на основі дельта-правила розробили ADALINE, який відразу почав використовуватися для завдань пророцтва і адаптивного управління. Зараз ADALINE (адаптивний суматор) є стандартним елементом багатьох систем обробки сигналів.
У 1961 році під керівництвом Бонгарда розроблена програма «Кора» : «.завдання Кори — пошук розділяючого правила після того, як знайдені оператори, що дають досить чіткі характеристики об'єкту або його частин».
У 1969 році Мінський публікує формальний доказ обмеженості перцептрона і показує, що він нездатний вирішувати деякі завдання, пов'язані з інваріантністю представлень. Інтерес до нейронних мереж різко спадає.
1974 рік — Пол Дж. Вербос, і А. І. Галушкін одночасно винаходять алгоритм зворотного поширення помилки для навчання багатошарових перцептронів.
1975 рік — Фукушима представляє Когнитрон — мережу, що самоорганізовується, призначену для інваріантного розпізнавання образів, але це досягається тільки за допомогою запам'ятовування практично усіх станів образу.
1982 рік — після тривалого занепаду, інтерес до нейромереж знову зростає. Хопфілд показав, що нейронна мережа із зворотними зв'язками може бути системою, що мінімізує енергію (так звана мережа Хопфілда). Кохоненом представлені моделі мережі, що навчається без учителя (нейронна мережа Кохонена).
1986 рік —Румельхартом, Хінтоном і Вільямсом та незалежно і одночасно Барцевим та Охониним перевідкритий та істотно розвинений метод зворотного поширення помилки. Почався вибух інтересу до навчаних нейронних мереж.
Штучний нейрон
Основними компонентами нейромережі є нейрони /neurons/ (елементи, вузли), які з’єднані зв’язками. Сигнали передаються по зваженим зв’язкам (connection), з кожним з яких пов’язаний ваговий коефіцієнт (weighting coefficient) або вага.
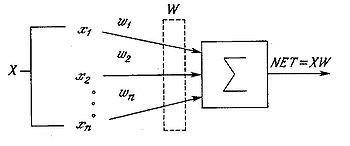
Моделі НМ – програмні і апаратні, найбільш поширені – програмні.Використання – розпізнавання образів, прогнозування, створення асоціативної пам’яті. Штучний нейрон імітує в першому наближенні властивості біологічного нейрона. На вхід штучного нейрона поступає множина сигналів, які є виходами інших нейронів. Кожен вхід множиться на відповідну вагу, аналогічну його синаптичній силі, і всі виходи підсумовуються, визначаючи рівень активації нейрона. Хоча мережеві парадигми досить різноманітні, в основі майже всіх їх лежить ця конфігурація. Тут множина вхідних сигналів, позначених x1, x2,…, xn, поступає на штучний нейрон. Ці вхідні сигнали, в сукупності позначаються вектором X, відповідають сигналам, що приходять в синапси біологічного нейрона. Кожен сигнал множиться на відповідну вагу w1, w2,…, wn, і поступає на сумуючий блок, позначений Σ. Кожна вага відповідає «силі» одного біологічного синаптичного зв'язку (множина ваг в сукупності позначається вектором W). Сумуючий блок, який відповідає тілу біологічного нейрона, складає зважені входи алгебраїчно, створюючи вихід, який ми називатимемо NET.
Активіаційні функції
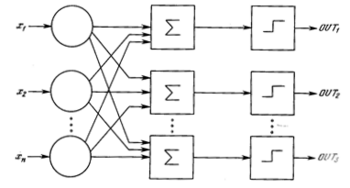
Сигнал NET далі, як правило, перетворюється активаційною функцією F і дає вихідний нейронний сигнал OUT = F(NET). Активаційна функція F(NET) може бути:
1. Пороговою бінарною функцією
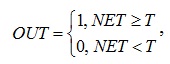
де Т – деяка постійна порогова величина, або ж функція, що точніше моделює нелінійну передавальну характеристику біологічного нейрона.
2. Лінійною обмеженою функцією
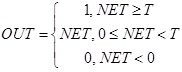
3. Функцією гіперболічного тангенса
де С > 0 – коефіцієнт ширини сигмоїди по осі абсцис (звичайно С=1).
4. Сигмоїдною (S-подібною) або логістичною функцією
З виразу для сигмоїда очевидно, що вихідне значення нейрона лежить в діапазоні [0,1]. Популярність сигмоїдної функції зумовлюють наступні її властивості:
- здатність підсилювати слабкі сигнали сильніше, ніж великі, і опиратися “насиченню” від потужних сигналів;
- монотонність і диференційованість на всій осі абсцис;
- простий вираз для похідної, що дає можливість використовувати широкий спектр оптимізаційних алгоритмів.
Персептрон
Перші персептрони були створені Ф.Розенблатом у 60-х роках і викликали великий інтерес. Первинна ейфорія змінилася розчаруванням, коли виявилося, що персептрони не здатні навчитися рішенню ряду простих задач. М.Мінський строго проаналізував цю проблему і показав, що є жорсткі обмеження на те, що можуть виконувати одношарові персептрони, і, отже, на те, чому вони можуть навчатися. Оскільки у той час методи навчання багатошарових мереж не були відомі, дослідники перейшли в більш багатообіцяючі області, і дослідження у області нейронних мереж прийшли в занепад. Відкриття методів навчання багатошарових мереж більшою мірою, ніж який-небудь інший чинник, вплинуло на відродження інтересу і дослідницьких зусиль.Навчання персептрона:
- Ініціалізація вагових матриць W (випадкові значення)
- Подати вхід X і обчислити вихід Y для цільового вектора YT
- Якщо вихід правильний – перейти на крок 4; інакше обчислити різницю D = YT – Y; модифікувати ваги за формулою:
wij(e+1) = wij(e) + α D Хі,
де wij(e) – значення ваги від нейрона i до нейрона j до налагодження, wij(e+1) – значення ваги після налагодження, α – коефіцієнт швидкості навчання, Хi – вхід нейрона i, e – номер епохи (ітерації під час навчання).
- Виконувати цикл з кроку 2, поки мережа не перестане помилятися. На другому кроці у випадковому порядку пред’являються всі вхідні вектори.
Один з найпесимістичніших результатів Мінського показує, що одношаровий персептрон не може відтворити таку просту функцію, як ВИКЛЮЧАЄ АБО. Це функція від двох аргументів, кожний з яких може бути нулем або одиницею. Вона приймає значення одиниці, коли один з аргументів рівний одиниці (але не обидва).