Відмінності між версіями «Профіль крила NACA»
Мар'яна (обговорення • внесок) |
Мар'яна (обговорення • внесок) |
||
| Рядок 90: | Рядок 90: | ||
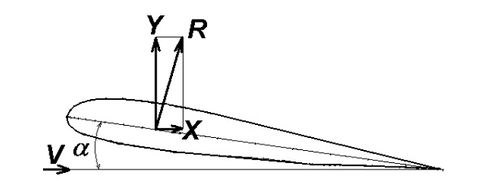
Головною аеродинамічній силою авіаційного профілю є вектор '''''R'''''. | Головною аеродинамічній силою авіаційного профілю є вектор '''''R'''''. | ||
| − | [[Файл:Рис1.jpg| | + | [[Файл:Рис1.jpg|500px|thumb|right|Вектор аеродинамічних сил]] |
Однак вектор '''''R''''' не представляє інтересу сам по собі. Практичний інтерес представляють його складові, вектора підйомної сили - '''''Y''''' і аеродинамічного опору - '''''X'''''. Напрям вектора '''''Y''''' перпендикулярно вектору швидкості '''''V'''''. Напрям вектора '''''X''''' збігається з вектором швидкості і завжди має позитивне значення. | Однак вектор '''''R''''' не представляє інтересу сам по собі. Практичний інтерес представляють його складові, вектора підйомної сили - '''''Y''''' і аеродинамічного опору - '''''X'''''. Напрям вектора '''''Y''''' перпендикулярно вектору швидкості '''''V'''''. Напрям вектора '''''X''''' збігається з вектором швидкості і завжди має позитивне значення. | ||
| Рядок 124: | Рядок 124: | ||
Формула, за якою обчислюється число Рейнольдса записується як: | Формула, за якою обчислюється число Рейнольдса записується як: | ||
| − | <math>{Re=\rho\cdot{V}\cdot{b}/\mu}</math> | + | <math>{Re=\rho\cdot{V}\cdot{b}/\mu}</math>; |
де <math>{V}</math> - швидкість (м / с), | де <math>{V}</math> - швидкість (м / с), | ||
| Рядок 136: | Рядок 136: | ||
Звідси, спростивши формулу, отримуємо: | Звідси, спростивши формулу, отримуємо: | ||
| − | <math>{Re\approx69000\cdot{V}\cdot{b}}</math> | + | <math>{Re\approx69000\cdot{V}\cdot{b}}</math>; |
Німецький професор Л. Прандтль, в результаті досліджень в 1918-1926 р, отримав формулу: | Німецький професор Л. Прандтль, в результаті досліджень в 1918-1926 р, отримав формулу: | ||
| − | <math>{C_{f}=2.656/\sqrt{Re}</math> | + | <math>{C_{f}=2.656/\sqrt{Re}</math>. |
Так як <math>C_{f}</math> включається як складова в <math>C_{x кр}</math>, то загальний опір крила, при зміні числа <math>{Re}</math>, так само буде змінюватися. Звідси можна зробити висновок, що при відомому числі <math>{Re}</math>, для обраного Вами профілю варто виконати розрахунок числа <math>{Re}</math> для Вашого літального апарату і при розбіжності чисел бодай на підлогу порядку, можна очікувати зміна аеродинамічних характеристик профілю. | Так як <math>C_{f}</math> включається як складова в <math>C_{x кр}</math>, то загальний опір крила, при зміні числа <math>{Re}</math>, так само буде змінюватися. Звідси можна зробити висновок, що при відомому числі <math>{Re}</math>, для обраного Вами профілю варто виконати розрахунок числа <math>{Re}</math> для Вашого літального апарату і при розбіжності чисел бодай на підлогу порядку, можна очікувати зміна аеродинамічних характеристик профілю. | ||
| Рядок 147: | Рядок 147: | ||
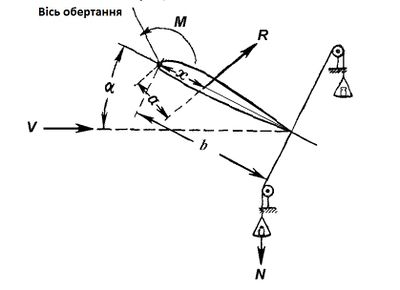
Аеродинамічна сила '''''R''''' складається з складові '''''Y''''' і '''''X'''''. Необхідно знати не тільки її величину, а й точку її додатки, інакше ми не зможемо добитися необхідного рівноваги крила у польоті. Точка прикладання сили '''''R''''' називається центром тиску крила. Положення центру тиску знаходиться наступним чином, крило зміцнюється в аеродинамічній трубі так, що може вільно обертатися навколо осі, що проходить через носок крила (див. Рис2). До хвостовій частині крила кріпляться нитки, перекинуті через ролики і забезпечені чашками з вантажами. Впливаючи на крило повітряним потоком на певному куті атаки, матимемо силу '''''R''''', яка прагне повернути крило навколо осі. | Аеродинамічна сила '''''R''''' складається з складові '''''Y''''' і '''''X'''''. Необхідно знати не тільки її величину, а й точку її додатки, інакше ми не зможемо добитися необхідного рівноваги крила у польоті. Точка прикладання сили '''''R''''' називається центром тиску крила. Положення центру тиску знаходиться наступним чином, крило зміцнюється в аеродинамічній трубі так, що може вільно обертатися навколо осі, що проходить через носок крила (див. Рис2). До хвостовій частині крила кріпляться нитки, перекинуті через ролики і забезпечені чашками з вантажами. Впливаючи на крило повітряним потоком на певному куті атаки, матимемо силу '''''R''''', яка прагне повернути крило навколо осі. | ||
| + | |||
| + | [[Файл:Рис2.jpg|400px|thumb|right|Величина і напрям сили '''''R''''' визначаються діагоналлю паралелограма, побудованого на силах '''''Y''''' і '''''X'''''.]] | ||
| + | |||
| + | Це обертання буде, очевидно, тим сильніше, чим більше сила <math>{R}</math> і плече <math>{a}</math>, т. е. Чим більше твір <math>{R\cdot{a}}</math>, зване - аеродинамічним моментом '''''(M)'''''. Щоб утримати крило в рівновазі, потрібно покласти на одну з чашок відповідний вантаж <math>{N}</math>. З механіки відомо, що цей вантаж повинен бути в стільки разів менше сили <math>{R}</math>, у скільки разів плече <math>{t}</math> більше плеча <math>{а}</math>. Іншими словами, має місце рівність: | ||
| + | |||
| + | <math>{M=R\cdot{a}=N\cdot{t}</math>, | ||
| + | |||
| + | Для того, щоб знайти плече <math>{a}</math>: | ||
| + | |||
| + | <math>{a=M/R=(N\cdot{t})/R</math>, | ||
| + | |||
| + | а потім вже і ту точку на хорді крила, через яку проходить сила <math>{R}</math>. Отже, ми знайшли положення центру тиску крила, яке | ||
| + | прийнято визначати величиною <math>{х}</math>, що дає відстань центру тиску від носка крила. | ||
| + | |||
| + | Аеродинамічні лабораторії, поряд з визначенням поляр для крил або профілів, виробляють випробування на визначення їх моменту. Як результатів таких випробувань виводяться не самі моменти, а їх коефіцієнти <math>{C_{m}}</math>, які пов'язані з першими наступною формулою: | ||
| + | |||
| + | <math>{M=C_{m}\cdot\rho\cdot{S}\cdot{V^2}\cdot{t/2}}</math>, | ||
| + | |||
| + | де <math>{\rho}</math>, <math>{S}</math>, <math>{V}</math> - величини щільності повітря, площі крила і швидкості потоку; | ||
| + | |||
| + | <math>{t}</math> - довжина хорди крила в метрах; | ||
| + | |||
| + | <math>{C_{m}}</math> — коефіцієнт моменту - число, залежне від профілю крила, кута атаки і тієї точки, щодо якої момент визначається. | ||
| + | |||
| + | Приймаючи до уваги, що | ||
| + | |||
| + | <math>{M=C_{m}\cdot\rho\cdot{S}\cdot{V^2}\cdot{t/2}}</math>, | ||
| + | |||
| + | а | ||
| + | |||
| + | <math>{R=C_{r}\cdot\rho\cdot{S}\cdot{V^2/2}}</math>, | ||
| + | |||
| + | знаючи вираз для плеча: <math>{a=M/R},</math> | ||
| + | |||
| + | що після скорочення на <math>{(\rho\cdot{S}\cdot{V^2/2})}</math>, отримуємо: <math>{{a}={t}\cdot{C_{m}/C_{y}}}</math>, | ||
| + | |||
| + | У межах невеликих кутів атаки (0 - 15 °), т. е. Тих кутів, з якими доводиться мати справу в польоті, величина <math>{С_{r}}</math> дуже не набагато відрізняється від | ||
| + | <math>{С_{у}}</math> і плече <math>{а}</math> від величини <math>{х}</math>; тому з достатньою для практики точністю можна вважати, що <math>{x={t}\cdot{C_{m}/C_{y}}}</math>, або <math>{x/{t}={C_{m}/C_{y}}}</math>. | ||
| + | |||
| + | Вважаючи <math>{t}</math> рівний 1 отримуємо величину <math>{х}</math> у відносних одиницях, <math>{x={C_{m}/C_{y}}}</math>. | ||
| + | |||
| + | Наведемо приклад, для наочності. Якщо авіаційний профіль, при куті атаки в 12 °, має <math>{C_{t}=0,109}</math>, а <math>{С_{y}=0,433}</math>, то точка прикладання сили <math>{R}</math> можна обчислити як <math>{x={C_{m}/C_{y}}=0,109/0,433=0,258}</math>. | ||
Версія за 19:17, 28 листопада 2015
Зміст
Профіль NACA
Серії профілів NACA (Національний авіаційний консультативний комітет США) стали позначати ім'ям організації і чотирма цифрами. Пізніше виникла необхідність збільшити кількість цифр до п'яти і більше.
Система 4-х символьної нумерації заснована на геометричних параметрах.
Приклад профіль NACA 6409 з чотирьох символьним позначенням:
- перша цифра позначає максимальну кривизну середньої
лінії - 6%;
- друга цифра позначає точку на хорді максимальної
кривизну середньої лінії від передньої кромки, в десятих частках від хорди - 0.4 (40%);
- третя і четверта цифри позначають товщину профілю - 09%.
Приклад профіль NACA 23015 з п'яти символьним позначенням:
- перша цифра позначає кривизну середньої лінії - 2%;
- друга і третя цифри позначають точку на хорді максимальної кривизну середньої лінії - 30%;
- четверта та п'ята цифри позначають товщину профілю - 15%.
Розвиток прикладної аеродинаміки призвело до появи ламінованих профілів, змінилися і позначення профілів. Так профіль NACA64 А2-215 читається як:
- 6 - серія профілю;
- 4 - протяжність ламінарного обтікання (40%);
- А - тип задньої частини профілю (керована);
- 2 - індекс 2, ширина ламінарної області в частках (Сy = ± 0,2) профілю;
- 2 - середина області ламінарного обтікання і низького опору, в частках (Сy = 0,2) профілю;
- 15 - дві цифри позначають товщину профілю - 15%.
Профіль Gö.
Серія профілів розроблена в Німеччині, в лабораторії міста Геттінген. У своїй символіці має ім'я - Gö і порядковий номер. Серія була досліджена в аеродинамічній трубі для низьких чисел Рейнольдса і з успіхом може бути використана для розрахунків авіамоделей. Профілю Е. Серія профілів розроблена професором Епплер, в Геттенгене. Серія розроблена для низьких чисел Рейнольдса, 40 000-200 000. Позначаються буквою Е і порядковим номером.
Профіль FX.
Профілю розроблені професором Вортманна. Профіль розшифровується як: FX - ініціали автора, 62 - рік створення профілю, К - позначення профілю з відхиляється крайкою, 131 - товщина профілю 13,1%.
Профіль B.
Профіль розроблений Бенедека. Профіль В-6358, читається як: В - ім'я профілю, 6 - товщина профілю в%, 35 - положення стрілки угнутості в%, 8 - відносна увігнутість в%.
Геометричні характеристики авіаційного профілю.
Дуже зручною, для геометричних характеристик авіаційних профілів, виявилася система відносних розмірів, у відсотках. Неподільний розмір - хорда профілю, є основою основ всіх геометричних розмірів.
Профілі авіаційних крил різноманітні, але їх можна класифікувати за геометричними ознаками як: 1) симетричні; 2) двояко опуклі; 3) опукло увігнуті; 4) плоско опуклі; 5) S - образні.
Для всіх цих профілів існують загальні геометричні параметри:
- b - довжина хорди профілю,
- с - товщина профілю,
- f - увігнутість профілю,
- r - радіус носика профілю,
- xc - координата найбільшої товщини, щодо носка профілю,
- xf - координата найбільшою угнутості, щодо носка профілю.
Деякі визначення:
Хорда профілю - умовна лінія, що з'єднує саму передню і саму задню точки профілю.
Увігнутість профілю - відстань, що вимірюється між середньою лінією профілю і його хордою.
Середня лінія профілю - геометричне місце точок, розташованих посередині ординат, перпендикулярних хорді і обмежених верхніми і нижніми контурами профілю.
Зазвичай ці параметри представляють у вигляді часток хорди - b. Це дуже зручно при побудові профілю з різною хордою, наприклад у еліптичного крила.
Для побудови профілю наводяться таблиці, з величинами x - відстань від носка профілю (у відносних одиницях, від 0 до 1, або відсотках), y (в) - координата верхньої точки і у (н) - координата нижньої точки профілю (так само в відносних одиницях або відсотках).
За товщиною профілю діляться на тонкі - з менше 8%, середні - з від 8% до 12% і товсті - з більш 12%. Залежно від угнутості середньої лінії розрізняють профілі: з малою увігнутістю - f менше 1,5%, із середньою увігнутістю - f 1,5 ÷ 4% і великий увігнутістю - f більше 4%.
Аеродинамічні характеристики авіаційного профілю.
Головною аеродинамічній силою авіаційного профілю є вектор R.
Однак вектор R не представляє інтересу сам по собі. Практичний інтерес представляють його складові, вектора підйомної сили - Y і аеродинамічного опору - X. Напрям вектора Y перпендикулярно вектору швидкості V. Напрям вектора X збігається з вектором швидкості і завжди має позитивне значення.
Аеродинамічні сили Y і X залежать від кута атаки [math]{\alpha}[/math], через відповідні безрозмірні коефіцієнти [math]{C_{x}}[/math] і [math]{C_{y}}[/math].
[math]{Y=C_{y}\cdot\rho\cdot{V^2}\cdot{S/2}}[/math]
[math]{X=C_{x}\cdot\rho\cdot{V^2}\cdot{S/2}}[/math]
Немаловажним параметром профілю є його аеродинамічна якість - К. Аеродинамічна якість залежить від кута атаки профілю. Обчислюється як співвідношення К[math]{\Kappa={Y/X}}[/math]. Виконавши деякі перетворення отримаємо К[math]{\Kappa={C_{y}/C_{x}}}[/math]. Аеродинамічна якість профілів має дуже широкий діапазон, від декількох одиниць і майже до 300. Прикладом такого профілю, з високою якістю, може служити профіль NASA 27-2012 створений І.Джекобсом в кінці 30-х років. Але не варто спокушатися з приводу застосування таких профілів на практиці. Вони вимагають дуже ретельного виготовлення і показують високий аеродинамічний якість тільки в обмежених умовах по турбулентності набігаючого потоку і числах Рейнольдса.
Невеликий відступ щодо профільного опору. У реальних умовах важко передбачити точний його значення, так як воно в значній мірі залежить від якості обробки поверхні крила. Дослідження проведені американськими вченими Абботом, Денхофом і Стіверсоном показали, що опір гладкого профілю з товщиною 24% може бути менше, ніж у шорсткого товщиною 6%. Дослідження проводилися з такими серіями профілів, як NASA 00, 14, 24, 230. Під шорсткістю приймалися нерівності ≈ 0,2..0,3 мм, на передній кромці профілю при хорді профілю 24 дюйма (приблизно 610 мм).
Індуктивний опір.
Індуктивний опір має чимале значення при розрахунках якості крила. На величину [math]{C_{xi}}[/math] - індуктивний опір, впливає подовження крила [math]{\lambda}[/math]. Зв'язок між цими величинами записується:
[math]{C_{xi}={{C_{y}}^2/\pi\lambda}[/math]
Отже коефіцієнт опору реального крила обчислюється:
[math]{C_{x}=C_{x пр}+C_{xi}}[/math]
Подовження реального крила літака може відрізнятися від крила моделі продувається в аеродинамічній трубі. Коефіцієнт опору крил:
[math]{C_{x кр}=C_{x0}+\DeltaC_{xi}}[/math]
Число Рейнольдса.
Число Рейнольдса, яке присутнє в характеристиках профілів тісно пов'язане з коефіцієнтом сили опору тертя [math]C_{f}[/math]. Обтікання повітрям тіла сильно залежить від характеру зміни швидкості в прикордонному шарі. При малих швидкостях і лінійних розмірах поверхні обтічний повітря в прикордонному шарі має плавне струминне протягом, зване ламінарним. При підвищенні швидкості і лінійних розмірах обтічного тіла плавність перебігу порушується і струменя починають перемішуватися. Таке, протягом в прикордонному шарі називається турбулентним. Не вдаючись у теоретичні викладки можна сказати, що зі збільшенням числа Рейнольдса сила тертя [math]C_{f}[/math] зменшується.
Формула, за якою обчислюється число Рейнольдса записується як:
[math]{Re=\rho\cdot{V}\cdot{b}/\mu}[/math];
де [math]{V}[/math] - швидкість (м / с),
[math]{b}[/math] - хорда крила (м),
[math]{\rho}[/math] - щільність повітря, при нормальних умовах 0,125 кг,
[math]{\mu}[/math] - динамічна в'язкість повітря.
Звідси, спростивши формулу, отримуємо:
[math]{Re\approx69000\cdot{V}\cdot{b}}[/math];
Німецький професор Л. Прандтль, в результаті досліджень в 1918-1926 р, отримав формулу:
[math]{C_{f}=2.656/\sqrt{Re}[/math].
Так як [math]C_{f}[/math] включається як складова в [math]C_{x кр}[/math], то загальний опір крила, при зміні числа [math]{Re}[/math], так само буде змінюватися. Звідси можна зробити висновок, що при відомому числі [math]{Re}[/math], для обраного Вами профілю варто виконати розрахунок числа [math]{Re}[/math] для Вашого літального апарату і при розбіжності чисел бодай на підлогу порядку, можна очікувати зміна аеродинамічних характеристик профілю.
Аеродинамічний момент крила.
Аеродинамічна сила R складається з складові Y і X. Необхідно знати не тільки її величину, а й точку її додатки, інакше ми не зможемо добитися необхідного рівноваги крила у польоті. Точка прикладання сили R називається центром тиску крила. Положення центру тиску знаходиться наступним чином, крило зміцнюється в аеродинамічній трубі так, що може вільно обертатися навколо осі, що проходить через носок крила (див. Рис2). До хвостовій частині крила кріпляться нитки, перекинуті через ролики і забезпечені чашками з вантажами. Впливаючи на крило повітряним потоком на певному куті атаки, матимемо силу R, яка прагне повернути крило навколо осі.
Це обертання буде, очевидно, тим сильніше, чим більше сила [math]{R}[/math] і плече [math]{a}[/math], т. е. Чим більше твір [math]{R\cdot{a}}[/math], зване - аеродинамічним моментом (M). Щоб утримати крило в рівновазі, потрібно покласти на одну з чашок відповідний вантаж [math]{N}[/math]. З механіки відомо, що цей вантаж повинен бути в стільки разів менше сили [math]{R}[/math], у скільки разів плече [math]{t}[/math] більше плеча [math]{а}[/math]. Іншими словами, має місце рівність:
[math]{M=R\cdot{a}=N\cdot{t}[/math],
Для того, щоб знайти плече [math]{a}[/math]:
[math]{a=M/R=(N\cdot{t})/R[/math],
а потім вже і ту точку на хорді крила, через яку проходить сила [math]{R}[/math]. Отже, ми знайшли положення центру тиску крила, яке прийнято визначати величиною [math]{х}[/math], що дає відстань центру тиску від носка крила.
Аеродинамічні лабораторії, поряд з визначенням поляр для крил або профілів, виробляють випробування на визначення їх моменту. Як результатів таких випробувань виводяться не самі моменти, а їх коефіцієнти [math]{C_{m}}[/math], які пов'язані з першими наступною формулою:
[math]{M=C_{m}\cdot\rho\cdot{S}\cdot{V^2}\cdot{t/2}}[/math],
де [math]{\rho}[/math], [math]{S}[/math], [math]{V}[/math] - величини щільності повітря, площі крила і швидкості потоку;
[math]{t}[/math] - довжина хорди крила в метрах;
[math]{C_{m}}[/math] — коефіцієнт моменту - число, залежне від профілю крила, кута атаки і тієї точки, щодо якої момент визначається.
Приймаючи до уваги, що
[math]{M=C_{m}\cdot\rho\cdot{S}\cdot{V^2}\cdot{t/2}}[/math],
а
[math]{R=C_{r}\cdot\rho\cdot{S}\cdot{V^2/2}}[/math],
знаючи вираз для плеча: [math]{a=M/R},[/math]
що після скорочення на [math]{(\rho\cdot{S}\cdot{V^2/2})}[/math], отримуємо: [math]{{a}={t}\cdot{C_{m}/C_{y}}}[/math],
У межах невеликих кутів атаки (0 - 15 °), т. е. Тих кутів, з якими доводиться мати справу в польоті, величина [math]{С_{r}}[/math] дуже не набагато відрізняється від [math]{С_{у}}[/math] і плече [math]{а}[/math] від величини [math]{х}[/math]; тому з достатньою для практики точністю можна вважати, що [math]{x={t}\cdot{C_{m}/C_{y}}}[/math], або [math]{x/{t}={C_{m}/C_{y}}}[/math].
Вважаючи [math]{t}[/math] рівний 1 отримуємо величину [math]{х}[/math] у відносних одиницях, [math]{x={C_{m}/C_{y}}}[/math].
Наведемо приклад, для наочності. Якщо авіаційний профіль, при куті атаки в 12 °, має [math]{C_{t}=0,109}[/math], а [math]{С_{y}=0,433}[/math], то точка прикладання сили [math]{R}[/math] можна обчислити як [math]{x={C_{m}/C_{y}}=0,109/0,433=0,258}[/math].