Відмінності між версіями «Капілярний тиск»
| Рядок 1: | Рядок 1: | ||
| + | |||
Бабурнич Іван, КТс-31 | Бабурнич Іван, КТс-31 | ||
| − | '''Визначення''' | + | |
| + | == '''Визначення''' == | ||
| + | |||
---- | ---- | ||
| Рядок 7: | Рядок 10: | ||
Капіля́рний тиск (рос. давление капиллярное; англ. capillary pressure, нім. Kapillardruck m) – різниця тисків (±Δp), що виникає внаслідок впливу сил поверхневого натягу на рівновагу або рух вільної поверхні рідини, границі рідини з твердим тілом, а також границі поділу між незмішуваними рідинами, окремий випадок поверхневих явищ. | Капіля́рний тиск (рос. давление капиллярное; англ. capillary pressure, нім. Kapillardruck m) – різниця тисків (±Δp), що виникає внаслідок впливу сил поверхневого натягу на рівновагу або рух вільної поверхні рідини, границі рідини з твердим тілом, а також границі поділу між незмішуваними рідинами, окремий випадок поверхневих явищ. | ||
| − | '''Визначення''' | + | |
| + | == '''Визначення''' == | ||
| + | |||
---- | ---- | ||
| Рядок 13: | Рядок 18: | ||
Прикладом капіярного явища є піднімання змочувальної або опускання незмочувальної рідини в капілярних (тонких) трубках чи порах твердого тіла (мал).[[Файл:123.jpg]] | Прикладом капіярного явища є піднімання змочувальної або опускання незмочувальної рідини в капілярних (тонких) трубках чи порах твердого тіла (мал).[[Файл:123.jpg]] | ||
| − | '''Пояснення''' | + | |
| + | == '''Пояснення''' == | ||
| + | |||
---- | ---- | ||
Версія за 12:39, 14 листопада 2015
Бабурнич Іван, КТс-31
Визначення
Капіля́рний тиск (рос. давление капиллярное; англ. capillary pressure, нім. Kapillardruck m) – різниця тисків (±Δp), що виникає внаслідок впливу сил поверхневого натягу на рівновагу або рух вільної поверхні рідини, границі рідини з твердим тілом, а також границі поділу між незмішуваними рідинами, окремий випадок поверхневих явищ.
Визначення
Прикладом капіярного явища є піднімання змочувальної або опускання незмочувальної рідини в капілярних (тонких) трубках чи порах твердого тіла (мал).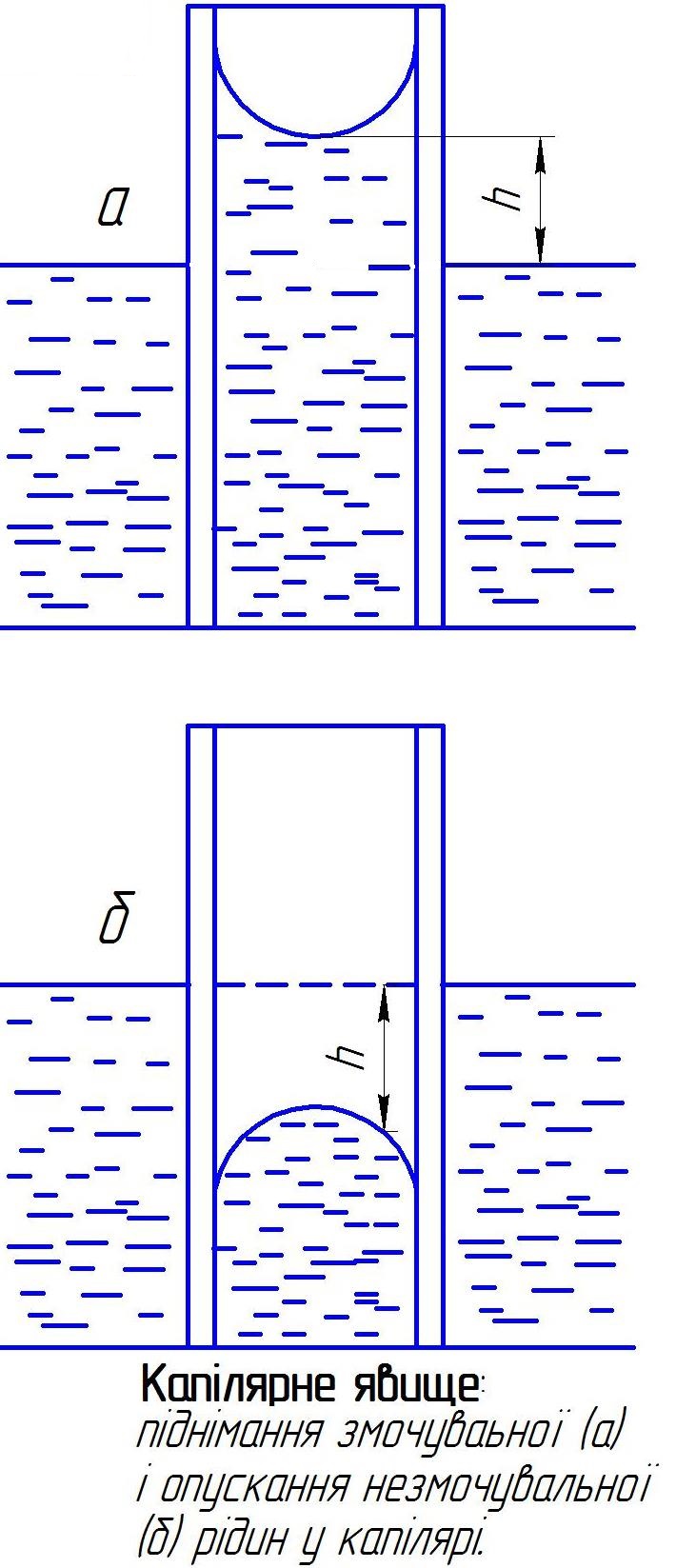
Пояснення
Ці явища зумовлені виникненням капілярного тиску ρ, зв'язаного з поверхневим натягом σ формулою Лапласа: ρ = 2σ/r, де r — радіус кривини поверхні рідини. Для змочувальних рідин р є додатною величиною, для не змочувальних — від'ємною. Висота h підняття змочувальної (опускання незмочувальної) рідини визначається: h = 2σ/(р1 — р2) rg, де g — прискорення вільного падіння, ρ1 і р2 — густини відповідно рідини та її пари. К. я. відіграють значну роль в природі, особливо у водному режимі грунтів та в обміні речовин рослин. Широко застосовуються в техніці (напр., у процесах сушіння, просочування тощо)