Відмінності між версіями «Нормальний закон розподілу»
| Рядок 7: | Рядок 7: | ||
</td></tr> | </td></tr> | ||
<tr> | <tr> | ||
| − | <td> Імя </td><td> | + | <td> Імя </td><td> Максим |
</td></tr> | </td></tr> | ||
<tr> | <tr> | ||
| − | <td> Прізвище </td><td> | + | <td> Прізвище </td><td> Федчук |
</td></tr> | </td></tr> | ||
<tr> | <tr> | ||
Поточна версія на 10:31, 20 березня 2012
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
| Імя | Максим | |
| Прізвище | Федчук | |
| По-батькові | Ігорович | |
| Факультет | ФІС | |
| Група | СН-51 | |
Зміст
Загальні положення
Нормальний розподіл виражає закономірності зміни значень змінних під впливом багатьох випадково виникаючих факторів, які діють у різних напрямах так, що жоден з них не впливає на інший.
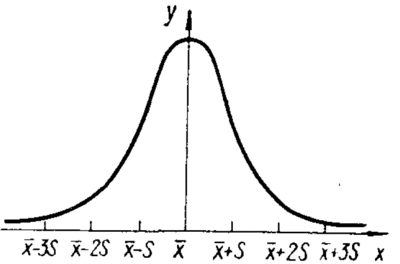
Крива нормального розподілу
Крива нормального розподілу імовірностей симетрична відносно осі y - найбільшої ординати, що відповідає середньому арифметичному [math]\bar x[/math] розглянутої змінної x. Точки перетину мають абсциси, які дорівнюють середньому квадратичному відхиленню цієї змінної, тобто [math]x_1=x-S[/math] та [math]x_2=\bar x + S[/math]. Ординати обох віток кривої спадають від найбільшої спочатку швидко, а потім повільніше і повільніше. Крива досягає значення у=0 при [math]x=\pm \infty[/math]. Проте значеннями ординати при [math]x=\bar x \pm 3S[/math] можна практично знехтувати. Крива нормального розподілу описується рівнянням
[math]y=\phi(x)=\frac{1}{S\sqrt{2\pi}}\exp \biggl[ -\frac{1}{2}(\frac{x-\bar x}{S})^2\biggr][/math],
де у - ордината точки кривої розподілу при заданому значенні розглядуваної змінної x. Із зменшенням СКВ крива нормального розподілу стає більш вузькою, витягнутою вгору, і навпаки, зі збільшенням S - розмитою і максимальне значення y зменшується. Замінивши [math]u=\frac{x - \bar x}{s}[/math] і вважаючи S=1, отримуємо рівняння кривої нормального розподілу нормованої випадкової величини:
[math]\phi(u)=\frac{1}{S\sqrt{2\pi}}\exp (-\frac{u^2}{2})[/math].
Якщо обґрунтовується припущення, що випадкова величина у генеральній сукупності розподілена нормально, вирівнюючі відносні частоти знаходять за формулою
[math]p_i=\frac{d}{S}\phi (u)[/math]
а вирівнюючі частоти - за формулою
[math]N_i=\frac{Nd}{S}\phi (u)[/math].
Ці залежності дають змогу побудувати нормальну криву за дослідними даними. Побудова такої кривої здійснюється з припущення, що в генеральній сукупності, число членів якої N може бути як завгодно великим, СКВ [math]\sigma[/math] дорівнює вибірковому S, а середнє арифметичне значення генеральної сукупності або математичне сподівання M[x] дорівнює середньому значенню x, утвореному з даної вибірки.
Порядок обчислення ординат кривої нормального розподілу
- Визначають вибіркові характеристики [math]\bar x[/math] та S;
- підраховують значення відхилень [math]x_m^*-\bar x[/math] і нормованих відхилень [math]u=(x_m^*-\bar x)/S[/math]
- знаходять за відповідною таблицею значення [math]\phi(u)[/math], що відповідають обчисленим u, і множать на загальне для даного розподілу відношення d/S або Nd/S (де d - ширина інтервалу);
- відкладають для відповідних абсцис змінних обчислені ординати [math]p_t^'[/math] або [math]N_t^'[/math].
Властивості нормального розподілу
Нормальний розподіл належить до унімодальних. Це означає, що існує єдине значення змінної, імовірність якого найбільша, і воно називається модою. Нормальний розподіл є симетричним, тобто для нього збігаються значення середнього арифметичного, медіани та моди і має властивість лінійності. У даному випадку це означає, що коли незалежні змінні [math]x_1[/math] і [math]x_2[/math] мають нормальний розподіл, то для довільних сталих чисел [math]\alpha[/math] i [math]\beta[/math] змінна [math]\alpha x_1 + \beta x_2[/math] також має нормальний розподіл.
Використана література
Математичне планування експериментів в АПК / В. О. Аністратенко, В. Г. Федоров.-К.:Вища школа,1993.-374с.