Відмінності між версіями «Метод Девідона – Флетчера – Пауела»
| Рядок 177: | Рядок 177: | ||
Проведено доведення по індукції. При j = 1 матриця D1 симетрична і позитивно визначена по умові леми. Крім того, <math></math>, оскільки D1 позитивно визначена. Тоді по теоремі 1 вектор d1 визначає напрям спуску. Передбачимо, що затвердження леми справедливе для деякого <math></math>, і покажемо, що воно справедливе для j+1. Хай x – ненульовий вектор з En, тоді з (1) маємо (4) Оскільки Dj – симетрична позитивно певна матриця, то існує позитивно певна матриця <math></math>, така, що <math></math>. Хай <math></math> і <math></math>. Тоді <math></math>, <math></math> і <math> | Проведено доведення по індукції. При j = 1 матриця D1 симетрична і позитивно визначена по умові леми. Крім того, <math></math>, оскільки D1 позитивно визначена. Тоді по теоремі 1 вектор d1 визначає напрям спуску. Передбачимо, що затвердження леми справедливе для деякого <math></math>, і покажемо, що воно справедливе для j+1. Хай x – ненульовий вектор з En, тоді з (1) маємо (4) Оскільки Dj – симетрична позитивно певна матриця, то існує позитивно певна матриця <math></math>, така, що <math></math>. Хай <math></math> і <math></math>. Тоді <math></math>, <math></math> і <math> | ||
</math>. Підставляючи ці вирази в (4), отримуємо : (5) По нерівності Шварця маємо <math></math>. Так, щоб довести, що<math><math>Вставте сюди формулу</math</math>, досить показати, що <math></math> і <math></math>. З (2) і (3) витікає, що <math></math>. (6) По припущенню <math></math>, і Dj позитивно визначена, так що | </math>. Підставляючи ці вирази в (4), отримуємо : (5) По нерівності Шварця маємо <math></math>. Так, щоб довести, що<math><math>Вставте сюди формулу</math</math>, досить показати, що <math></math> і <math></math>. З (2) і (3) витікає, що <math></math>. (6) По припущенню <math></math>, і Dj позитивно визначена, так що | ||
| + | |||
| + | [[Категорія:Планування експерименту]] | ||
Версія за 12:53, 26 лютого 2012
| Прізвище | Храплива |
| Ім'я | Уляна |
| По-батькові | Вікторівна |
| Факультет | ФІС |
| Група | СНм-51 |
| Залікова книжка | СНм-11-253 |
Розглянемо алгоритм Девідона - Флетчера - Пауелла мінімізації функції, що диференціюється, декілька змінних. Зокрема, якщо функція квадратична, то, як буде показано пізніше, метод виробляє зв'язані напрями і зупиняється після виконання однієї ітерації, тобто після пошуку уздовж кожного із зв'язаних напрямів.
Початковий етап
Нехай [math]\varepsilon \succ 0[/math] - константа для зупинки. Вибрати точку [math]{x_1}[/math] і початково симетричну позитивно визначену матрицю [math]{D_1}[/math]. Покласти [math]{y_1} = {x_1}[/math], k = j = 1 і перейти до основного етапу.
Основний етап
Крок 1. Якщо [math]\left\| {\left. {\nabla f({y_i})} \right\| \lt \varepsilon } \right.[/math], то зупинитися; в іншому випадку [math]{d_i} = - {D_i}\nabla f({y_i})[/math] і узяти в якості [math]{\lambda _i}[/math] оптимальне рішення задачі мінімізації [math]f({y_i} + \lambda {d_i})[/math] при [math]\lambda \ge 0[/math]. Покласти [math]{y_{i + 1}} = {y_i} + {\lambda _i}{d_i}[/math]. Якщо j < n, то перейти до кроку 2. Якщо j = n, то покласти [math]{y_1} = {x_{k + 1}} = {y_{n + 1}}[/math], замінити k на k+1, покласти j=1 і повторити крок 1.
Крок 2. Побудувати [math]{D_{j + 1}}[/math] таким чином:
Замінити j на j+1 і перейти до кроку 1.
Приклад
Мінімізувати [math]{({x_1} - 2)^4} + {({x_1} - 2{x_2})^2}.[/math]
Результати обчислень методом Девідона - Флетчера - Пауелла приведені в таблиці 1.
| k | [math]{x_k}[/math] [math]f({x_k})[/math] |
j | [math]{y_j}[/math] [math]f({y_j})[/math] |
[math]\nabla f({y_j})[/math] | [math]\left\| {\left. {\nabla f({y_j})} \right\|} \right.[/math] | D | [math]{d_j}[/math] | [math]{\lambda _j}[/math] | [math]{y_{j + 1}}[/math] |
|---|---|---|---|---|---|---|---|---|---|
| 1 | (0.00,3.00) (52.00) |
1 | (0.00,3.00) (52.00) |
(-44.00,24.00) | 50.12 | [math]$\left[ 1|0\\ 0|1 \right]$[/math] | (44.00,-24.00) | 0.062 | (2.70, 1.51) |
| 2 | (2.70,1.51) (0.34) |
(0.73,1.28) | 1.47 | [math]$\left[ 0.25|0.38\\ 0.38|0.71 \right]$[/math] | (-0.67,-1.31) | 0.22 | (2.55,1.22) | ||
| 2 | (2.55,1.22) (0.1036) |
1 | (2.55,1.22) (0.1036) |
(0.89,-0.44) | 0.99 | [math]$\left[ 1|0\\ 0|1 \right]$[/math] | (-0.89,0.44) | 0.11 | (2.45,1.27) |
| 2 | (2.45,1.27) (0.0490) |
(0.18,0.36) | 0.40 | [math]$\left[ 0.65|0.45\\ 0.45|0.46 \right]$[/math] | (-0.28,-0.25) | 0.64 | (2.27,1.11) | ||
| 3 | (2.27,1.11) (0,008) |
1 | (2.27,1.11) (0,008) |
(0.18,-0.20) | 0.27 | [math]$\left[ 1|0\\ 0|1 \right]$[/math] | (-0.18,0.20) | 0.10 | (2.25,1.13) |
| 2 | (2.25,1.13) (0.004) |
(0.04,0.04) | 0.06 | [math]$\left[ 0.80|0.38\\ 0.38|0.31 \right]$[/math] | (-0.05,-0.03) | 2.64 | (2.12,1.05) | ||
| 4 | (2.12,1.05) (0,0005) |
1 | (2.12,1.05) (0,0005) |
(0.05,-0.08) | 0.09 | [math]$\left[ 1|0\\ 0|1 \right]$[/math] | (-0.05,0.08) | 0.10 | (2.115,1.058) |
| 2 | (2.115,1.058) (0.0002) |
(0.004,0.004) | 0.006 |
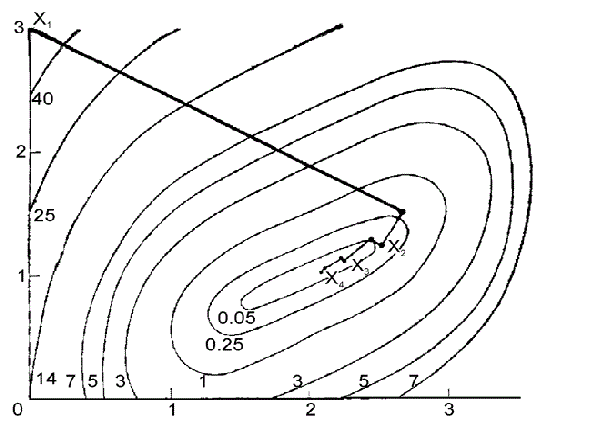
На кожній ітерації вектор[math]{d_j}[/math] для j=1,2 визначається у вигляді [math] - {D_j}\nabla f({y_j})[/math], де [math]{D_1}[/math] одинична матриця, а [math]{D_2}[/math] обчислюється по формулах (1) - (3). При k = 1 маємо [math]{p_1} = {(2.7, - 1.49)^T},{q_1} = {(44.73, - 22.72)^T}[/math]. На другій ітерації [math]{p_1} = {(-0.1, 0.05)^T},{q_1} = {(-0.7, 0.8)^T}[/math] і, нарешті, на третій ітерації [math]{p_1} = {(-0.02, 0.02)^T},{q_1} = {(-0.14, 0.24)^T}[/math]. Точка [math]{y_{j + 1}}[/math] обчислюється оптимізацією уздовж напряму [math]{d_j}[/math] при початковій точці [math]{y_j}[/math] для j = 1, 2. Процедура зупинена в точці [math]{y_2} = {(2.115, 1.058)^T}[/math] на четвертій ітерації оскільки норма [math]\left\| {\left. {f({y_2})} \right\| = 0.006} \right.[/math] досить мала. Траєкторія руху, отримана методом, показана на рисунку 1.
Рисунок 1 - Метод Дэвидона - Флетчера - Пауэлла.
Лема показує, що кожна матриця [math]{d_j}[/math] позитивно визначена і [math]{d_j}[/math] є напрямом спуску. Для доказу леми нам знадобиться :
Теорема 1. Нехай S - непорожня безліч в Еn, точка [math]x \in cl[/math] S. Конусом можливих напрямів в точці x називається безліч [math]D = \left\{ {d:d \ne 0,x + \lambda d \right \in S[/math]при всіх [math]\lambda \in (0,\delta )[/math] для деякого [math]\delta \gt 0}[/math].
Визначення.Нехай x і y - вектори з Еn і [math]\left| {{x^T}y} \right|[/math] - абсолютне значення скалярного відтворення [math]\left {{x^T}y} \right[/math]. Тоді виконується наступна нерівність, звана нерівністю Шварца:
Лема 1
Нехай [math]{y_1} \in {E_n}[/math], а [math]{D_1}[/math] – початкова позитивно певна симетрична матриця. Для j = 1 ..., n покладемо [math]{y_{j + 1}} = {y_j} + {\lambda _j}{d_j}[/math], де [math]{d_j} = - D\nabla f({y_j})[/math], а [math]{\lambda _j}[/math] є оптимальним рішенням задачі мінімізації [math]f({y_j} + \lambda {d_j})[/math] при [math]\lambda \ge 0[/math]. Нехай, крім того, для j = 1 ..., n – 1 матриця Dj+1 визначається по формулах (1) - (3). Якщо [math]\nabla f({y_j}) \ne 0[/math] для j = 1 ..., n, то матриці D1 ...,Dn симетричні і позитивно визначені, так що d1 ..., dn – напрями спуску.
Доведення
Проведено доведення по індукції. При j = 1 матриця D1 симетрична і позитивно визначена по умові леми. Крім того, [math][/math], оскільки D1 позитивно визначена. Тоді по теоремі 1 вектор d1 визначає напрям спуску. Передбачимо, що затвердження леми справедливе для деякого [math][/math], і покажемо, що воно справедливе для j+1. Хай x – ненульовий вектор з En, тоді з (1) маємо (4) Оскільки Dj – симетрична позитивно певна матриця, то існує позитивно певна матриця [math][/math], така, що [math][/math]. Хай [math][/math] і [math][/math]. Тоді [math][/math], [math][/math] і [math][/math]. Підставляючи ці вирази в (4), отримуємо : (5) По нерівності Шварця маємо [math][/math]. Так, щоб довести, що[math]\lt math\gt Вставте сюди формулу\lt /math[/math], досить показати, що [math][/math] і [math][/math]. З (2) і (3) витікає, що [math][/math]. (6) По припущенню [math][/math], і Dj позитивно визначена, так що