Відмінності між версіями «Симплексний метод оптимізації»
(Створена сторінка: {|border=2 style="float: right; margin-left: 1em; margin-bottom: 0.5em; width: 242px; border: #99B3FF solid 1px" |- | '''Прізвище''' || Храплива …) |
|||
| Рядок 14: | Рядок 14: | ||
|} | |} | ||
| − | == Основні | + | == Основні відомості == |
Головною особливістю симплексного методу є суміщення процесів вивчення поверхні відклику і пересування по ній. Це досягається тим, що n-вимірний симлекс - це опукла фігура, утворена n+1 точками (вершинами), що не належать одночасно жодному (n-1) - вимірному підпростору n-вимірного простору {Хn}. Очевидно, що число вершин симплексу на одиницю перевищує вимірність факторного простору. Так, на площині симплексом є трикутник, у тривимірному просторі - тетраедр тощо. Симплекс називається решулярним, якщо всі відстані між його вершинами рівні. | Головною особливістю симплексного методу є суміщення процесів вивчення поверхні відклику і пересування по ній. Це досягається тим, що n-вимірний симлекс - це опукла фігура, утворена n+1 точками (вершинами), що не належать одночасно жодному (n-1) - вимірному підпростору n-вимірного простору {Хn}. Очевидно, що число вершин симплексу на одиницю перевищує вимірність факторного простору. Так, на площині симплексом є трикутник, у тривимірному просторі - тетраедр тощо. Симплекс називається решулярним, якщо всі відстані між його вершинами рівні. | ||
| Рядок 20: | Рядок 20: | ||
Якщо провести експерименти у вершинах симплексу, то можна знайти напрям максимального нахилу поверхні відклику на підставі зроблених замірів, як такий, що проходить з центра симплексу через грань, протилежну вершині з мінімальним значенням виходу y(x). Тому для пересування до екстремуму переходять від вихідного симплексу до симплексу, що міститься в області вищого значення відклику, шляхом відхилення вершини з мінімальним виходом y(x) та побудови регулярного симплексу з новою вершиною, що є через симетрію дзеркальним відбиттям відкинутої. Потім процес відкидання вершини з найгіршим відкликом та побудови нового симплексу повторюється, внаслідок чого формується ланцюжок симплексів, які пересуваються у факторному просторі до точки екстремуму. <br> | Якщо провести експерименти у вершинах симплексу, то можна знайти напрям максимального нахилу поверхні відклику на підставі зроблених замірів, як такий, що проходить з центра симплексу через грань, протилежну вершині з мінімальним значенням виходу y(x). Тому для пересування до екстремуму переходять від вихідного симплексу до симплексу, що міститься в області вищого значення відклику, шляхом відхилення вершини з мінімальним виходом y(x) та побудови регулярного симплексу з новою вершиною, що є через симетрію дзеркальним відбиттям відкинутої. Потім процес відкидання вершини з найгіршим відкликом та побудови нового симплексу повторюється, внаслідок чого формується ланцюжок симплексів, які пересуваються у факторному просторі до точки екстремуму. <br> | ||
Рух симплексу по поверхні відклику для двофакторної задачі проїлюстровано на рис. 1, а.<br> | Рух симплексу по поверхні відклику для двофакторної задачі проїлюстровано на рис. 1, а.<br> | ||
| + | |||
| + | == Алгоритм симплексного планування == | ||
''Симплексне планування виконується за таким алгоритмом:'' | ''Симплексне планування виконується за таким алгоритмом:'' | ||
Поточна версія на 00:34, 21 лютого 2012
| Прізвище | Храплива |
| Ім'я | Уляна |
| По батькові | Вікторівна |
| Факультет | ФІС |
| Група | СНм-51 |
Основні відомості
Головною особливістю симплексного методу є суміщення процесів вивчення поверхні відклику і пересування по ній. Це досягається тим, що n-вимірний симлекс - це опукла фігура, утворена n+1 точками (вершинами), що не належать одночасно жодному (n-1) - вимірному підпростору n-вимірного простору {Хn}. Очевидно, що число вершин симплексу на одиницю перевищує вимірність факторного простору. Так, на площині симплексом є трикутник, у тривимірному просторі - тетраедр тощо. Симплекс називається решулярним, якщо всі відстані між його вершинами рівні.
В основі застосування симплексу для цілей оптимізації лежить така його важлива властивість: з будь-якого симплексу можна, відкинувши одну з вершин і використовуючи залишену грань, дістати новий сиплекс, додавши всього лише одну точку. Шляхом послідовного відкидання вершин можна здійснювати пересування симплексу у факторному просторі, причому це пересування відбуватиметься при кожному наступному експерименті.
Якщо провести експерименти у вершинах симплексу, то можна знайти напрям максимального нахилу поверхні відклику на підставі зроблених замірів, як такий, що проходить з центра симплексу через грань, протилежну вершині з мінімальним значенням виходу y(x). Тому для пересування до екстремуму переходять від вихідного симплексу до симплексу, що міститься в області вищого значення відклику, шляхом відхилення вершини з мінімальним виходом y(x) та побудови регулярного симплексу з новою вершиною, що є через симетрію дзеркальним відбиттям відкинутої. Потім процес відкидання вершини з найгіршим відкликом та побудови нового симплексу повторюється, внаслідок чого формується ланцюжок симплексів, які пересуваються у факторному просторі до точки екстремуму.
Рух симплексу по поверхні відклику для двофакторної задачі проїлюстровано на рис. 1, а.
Алгоритм симплексного планування
Симплексне планування виконується за таким алгоритмом:
- з апріорних знань про процес задається крок варіювання Xi (i = 1,2,..., n) за кожним фактором Хі;
- задається розмір симплексу ρ, тобто відстань між двома вершинами в одиницях варіювання відповідних змінних; ρ - величина безрозмірна;
- проводиться орієнтація початкового симплексу. Для цього одна вершина С1 розміщується у вихідну точку X1-вектор. Положення решти вершин початкового симплексу визначається за допомогою векторів:
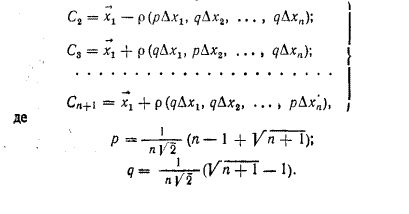
Положення початкового симплексу у факторном проторі для даних табл. 1 наведено на рис. 1, б;
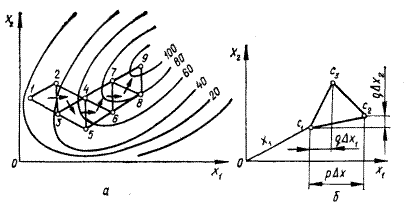
Таблиця 1 - Координати початкового симплексу
- реалізується експеримент у вершинах симплексу, тобто при варійованих параметрів Хі, що відповідають координатам С1,С2,...,Сn+1. Спостережені значення виходу у відповідних точках позначатимемо Yij, де і - номер симплексу, а j - номер вершини і-го симплексу;
- точка Сj, в якій спостерігається найгірший відклик, тобто виконується умова
відхиляється і знаходиться вершина Cl+1,j наступного симплексу - дзеркальне відбиття Cl,j відносно залишеної грані.
Координати Xi (i=1,2,...,n)точка Ci,j позначають Xl,j,i і обчислюють за формулами
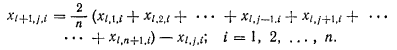
Якщо в результаті експерименту в двох вершинах симплексу буде однакове найгірше значення виходу
то рішення про дальший рух симплексу береться випадковим (наприклад, підкидання монети);
- проводиться експеримент у вершині Cl+1,j нового симплексу Cl+1,i; Cl+1,2;...;Cl+1,n+1, і його результати y+1 порівнюються зі значеннями виходу в решті вершин. Потім повторюється процедура відкидання вершини з мінімальним виходом.
Якщо значення Yi+1,j у щойно визначеній вершині знову буде мінімальним, то здійснюють повернення до вихідного симплексу і відкидання вершини з наступним по порядку мінімальним значенням виходу;
- критерієм виходу в район оптимуму є припинення поступального руху симплексу. Він починає обертання навколо однієї з вершин (одна і та точка зустрічається більше, ніж в n+1 послідовних симплексах). Подібна ситуація може виникнути у двох випадках:
- більш високий відклик в указаній точці дістали внаслідок впливу похибок експерименту. Тут повторний експеримент проявляє картину і пошук точки екстремуму продовжується в колишній послідовності;
- якщо в результаті експерименту в сумнівній точці знову дістали найвище у безпосередній близькості від точки екстремуму і пошук припиняється.
Список використаних джерел
Математичне планування експериментів в АПК / В.О. Аністратенко; В.Г. Федоров / Київ "Вища школа", 1993.