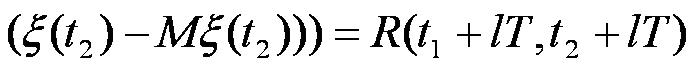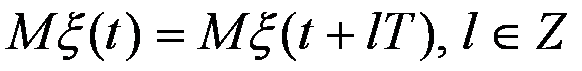Відмінності між версіями «Прогнозування»
Тетяна (обговорення • внесок) |
Тетяна (обговорення • внесок) |
||
| Рядок 45: | Рядок 45: | ||
==Лінійний випадковий періодичний процес== | ==Лінійний випадковий періодичний процес== | ||
Випадковий процес, інтегральне зображення якого має вигляд стохастичного інтегралу | Випадковий процес, інтегральне зображення якого має вигляд стохастичного інтегралу | ||
| − | [[Файл:Рисунок6.gif]] | + | <p>[[Файл:Рисунок6.gif]]<\p> |
називають лінійним випадковим процесом. У формулі детерміновану функцію φ(τ,t) є L2 (-∞,∞) називають ядром лінійного процесу, а η(τ), τєR η(0)=0, випадковий процес з незалежними приростами,- породжуючим процесом. | називають лінійним випадковим процесом. У формулі детерміновану функцію φ(τ,t) є L2 (-∞,∞) називають ядром лінійного процесу, а η(τ), τєR η(0)=0, випадковий процес з незалежними приростами,- породжуючим процесом. | ||
Модель лінійного випадкового періодичного процесу являє собою результат накладання великого числа елементарних імпульсі, що виникають у випадкові моменти часу τк, форма яких описується не випадковою функцією φ(τk,t), а їх амплітуди описуються не випадковими величинами . Варто зазначити, що лінійний випадковий процес який ми бачимо на слайді можна вважати періодичним за Слуцьким випадковим процесом лише за певних умов. | Модель лінійного випадкового періодичного процесу являє собою результат накладання великого числа елементарних імпульсі, що виникають у випадкові моменти часу τк, форма яких описується не випадковою функцією φ(τk,t), а їх амплітуди описуються не випадковими величинами . Варто зазначити, що лінійний випадковий процес який ми бачимо на слайді можна вважати періодичним за Слуцьким випадковим процесом лише за певних умов. | ||
<p>Ця є конструктивною, оскільки враховує механізм формування сигналу, дозволяє обґрунтувати його ергодичність, а також визначити параметри моделі за результатами експериментальних досліджень.</p> | <p>Ця є конструктивною, оскільки враховує механізм формування сигналу, дозволяє обґрунтувати його ергодичність, а також визначити параметри моделі за результатами експериментальних досліджень.</p> | ||
Версія за 17:21, 8 лютого 2012
Прогнозування — процес передбачення майбутнього стану предмета чи явища на основі аналізу його минулого і сучасного, систематична інформація про якісні й кількісні характеристики розвитку цього предмета чи явища в перспективі. Результатом прогнозування є прогноз — знання про майбутнє і про ймовірний розвиток сьогочасних тенденцій. Прогноз — це результат процесу прогнозування, виражений у текстовій, математичній, графічній або іншій формі судження про можливий стан об'єкта в майбутньому.
Зміст
Класифікації прогнозів за ознаками
- Залежно від тимчасового охоплення:
- короткостроковий прогноз — це прогноз строком до 1 місяця (наприклад,тижневі прогнози руху готівки);
- середньостроковий прогноз — це прогноз строком до 1 року (наприклад,місячні й квартальні прогнози темпів інфляції);
- довгостроковий або перспективний прогноз — це прогноз строком понад 1 рік (наприклад, прогноз змін інвестиційного клімату в країні).
- Залежно від типу прогнозування:
- пошуковий прогноз — це прогноз, отриманий методом наукового прогнозування від сьогодення до майбутнього;
- нормативний прогноз — це прогноз, отриманий методом нормативно-цільового прогнозування, у рамках якого спочатку визначаються цілі й орієнтири на майбутній період часу, а потім оцінюється розвиток об'єкта виходячи із цих орієнтирів;
- прогноз, заснований на творчому баченні — це прогноз, отриманий на основі суб'єктивних знань прогнозиста, його інтуїції.
- Залежно від можливості впливу на майбутнє:
- пасивний прогноз — це прогноз, що виходить із того, що в силу певних причин підприємство не має наміру впливати на об'єкт, і передбачається можливість самостійного, що не залежить від дій підприємства, розвитку зовнішніх процесів;
- активний прогноз — це прогноз, що передбачає можливість активного впливу підприємства на зовнішнє середовище.
- За ступенем імовірності:
- інваріантний прогноз — це прогноз, що включає тільки один варіант розвитку подій;
- варіантний прогноз — це прогноз, що ґрунтується на положенні про значний ступінь невизначеності зовнішнього середовища і який включає кілька ймовірних варіантів розвитку подій.
- За способом подання результатів:
- точковий прогноз — це прогноз, який допускає, що даний варіант має тільки одне єдине значення прогнозованого показника (наприклад, через 3 місяці ціна на позикові інвестиційні ресурси зросте на 3%);
- інтервальний прогноз — прогноз, у якому передбачається деякий діапазон значень прогнозованого показника (наприклад, через 3 місяці ціна на позикові інвестиційні ресурси зросте на 2,5-3,5%).
Аналіз часових рядів
Ритмічні сигнали в енергетиці
Ритмічні сигнали зустрічаються в акустиці, електро- і радіо техніці, авіації, астрономії, медицині, метеорології і найголовніше в енергетиці та ін. Широкий спектр застосування ритмічних сигналів ставить перед розробниками інформаційно-управляючих систем нові вимого що до створення відповідного апарата моделювання, та аналізу такого виду сигналів. Дослідження будь-якого сигналу виимагає побудови адекватної математичної моделі та розроблення на її основі методів статистичної обробки та імітаційного моделювання сигналів.
До математичного моделювання ритмічних сигналів існує два підходи:
- Детермінований
- Стохастичний
У випадку детермінованого підходу за математичну модель ритмічного сигналу приймають детерміновану періодичну функцію. Функцію f(t) називають періодичною, якщо існує таке число T>0, що f(t)=f(t+T), де Т – період функції.
У рамках стохастичного підходу виділяють такі моделі ритмічних сигналів:
- Адитивна;
- Мультиплікативна;
- Модель випадкового періодичного процесу за Слуцьким;
- Процес із незалежними Т-періодичними приростами;
- Модель періодично-корельованого випадкового процесу;
- Лінійний випадковий періодичний процес.
Зокрема дві наступні моделі зазвичай використовуються для бробки саме енергетичних сигналів. Це Модель періодично-корельованого випадкового процесу, та лінійний випадковий періодичний процес.
Модель періодично-корельованого випадкового процесу ПКВП
Періодично-корельованим називають процес ξ(t) з періодичними математичним сподіванням та кореляційною функцією
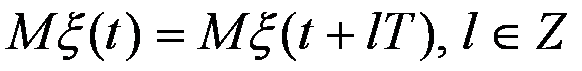
Використання ПКВП дало змогу розв'язати низку прикладних задач, пов'язаних зі статистичним аналізом ритмічних сигналів: оцінюванням їх математичного сподівання, дисперсії, кореляційної функції, спектральним аналізом. Поряд із суттєвими перевагами ця математична модель має і свої „мінуси". По-перше, ПКВП неможливо пов'язати з фізичними властивостями досліджуваного сигналу. Крім того така модель враховує періодичність лише перших двох моментальних функцій, і, як наслідок, дозволяє вивчати ритмічні сигнали тільки в рамках спектрально-кореляційної теорії. Вищі моментні функції та функції розподілу не можуть бути досліджені на її основі.
Лінійний випадковий періодичний процес
Випадковий процес, інтегральне зображення якого має вигляд стохастичного інтегралу
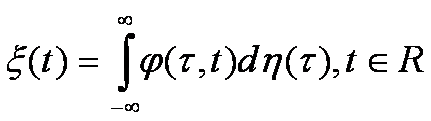 <\p>
називають лінійним випадковим процесом. У формулі детерміновану функцію φ(τ,t) є L2 (-∞,∞) називають ядром лінійного процесу, а η(τ), τєR η(0)=0, випадковий процес з незалежними приростами,- породжуючим процесом.
Модель лінійного випадкового періодичного процесу являє собою результат накладання великого числа елементарних імпульсі, що виникають у випадкові моменти часу τк, форма яких описується не випадковою функцією φ(τk,t), а їх амплітуди описуються не випадковими величинами . Варто зазначити, що лінійний випадковий процес який ми бачимо на слайді можна вважати періодичним за Слуцьким випадковим процесом лише за певних умов.
<p>Ця є конструктивною, оскільки враховує механізм формування сигналу, дозволяє обґрунтувати його ергодичність, а також визначити параметри моделі за результатами експериментальних досліджень.
<\p>
називають лінійним випадковим процесом. У формулі детерміновану функцію φ(τ,t) є L2 (-∞,∞) називають ядром лінійного процесу, а η(τ), τєR η(0)=0, випадковий процес з незалежними приростами,- породжуючим процесом.
Модель лінійного випадкового періодичного процесу являє собою результат накладання великого числа елементарних імпульсі, що виникають у випадкові моменти часу τк, форма яких описується не випадковою функцією φ(τk,t), а їх амплітуди описуються не випадковими величинами . Варто зазначити, що лінійний випадковий процес який ми бачимо на слайді можна вважати періодичним за Слуцьким випадковим процесом лише за певних умов.
<p>Ця є конструктивною, оскільки враховує механізм формування сигналу, дозволяє обґрунтувати його ергодичність, а також визначити параметри моделі за результатами експериментальних досліджень.