Відмінності між версіями «Особливості планування експериментів»
Mars (обговорення • внесок) |
Mars (обговорення • внесок) |
||
| Рядок 75: | Рядок 75: | ||
Покажемо, що моделі для планування експериментів є окремими випадками моделей лінійної регресії [21]. Знайдою середнє за всіма дослідами: | Покажемо, що моделі для планування експериментів є окремими випадками моделей лінійної регресії [21]. Знайдою середнє за всіма дослідами: | ||
<br> | <br> | ||
| − | <math>\mu =\frac{\sum\limits_{i\in I}^{{}}{{}}\sum\limits_{i\in I}^{{}}{{{\eta }_{ij}}}}{IJ}=\eta | + | <math>\mu =\frac{\sum\limits_{i\in I}^{{}}{{}}\sum\limits_{i\in I}^{{}}{{{\eta }_{ij}}}}{IJ}=\eta,</math> (3) |
<br> | <br> | ||
де крапка означає усереднення по всіх значеннях відповідного індексу. | де крапка означає усереднення по всіх значеннях відповідного індексу. | ||
| Рядок 84: | Рядок 84: | ||
Тоді αAi, - головний ефект фактора А на рівні і визначається як різниця між його середнім і загальним середнім: | Тоді αAi, - головний ефект фактора А на рівні і визначається як різниця між його середнім і загальним середнім: | ||
<br> | <br> | ||
| − | <math>\alpha _{i}^{A}={{A}_{i}}-\mu ={{\eta }_{j}}-\eta | + | <math>\alpha _{i}^{A}={{A}_{i}}-\mu ={{\eta }_{j}}-\eta .</math> (5) |
<br> | <br> | ||
З виразів (3)-(5) видно, що середнє головного ефекту дорівнює нулю, тому що | З виразів (3)-(5) видно, що середнє головного ефекту дорівнює нулю, тому що | ||
| Рядок 92: | Рядок 92: | ||
Головний ефект фактора В на рівні j визначаємо як | Головний ефект фактора В на рівні j визначаємо як | ||
<br> | <br> | ||
| − | <math>\alpha _{j}^{B}={{B}_{j}}-\mu =\frac{1}{I}\sum\limits_{i}{{{\eta }_{ij}}-\mu =\eta | + | <math>\alpha _{j}^{B}={{B}_{j}}-\mu =\frac{1}{I}\sum\limits_{i}{{{\eta }_{ij}}-\mu =\eta -\eta.}</math> (7) |
<br> | <br> | ||
Аналогічно | Аналогічно | ||
| Рядок 109: | Рядок 109: | ||
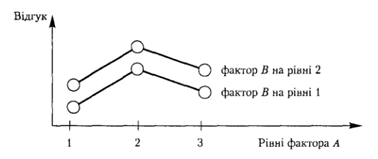
Відобразивши графічно, як фактор А впливає на рівень і фактора В, одержимо паралельні криві відгуку (рис. 1). Якщо є взаємодія між факторами А \ В, то змі¬на фактора А викликає різноманітні зміни відгуку на різних рівнях фактора В. Таку взаємодію між рівнями і та j факторів А, В відповідно визначаємо як | Відобразивши графічно, як фактор А впливає на рівень і фактора В, одержимо паралельні криві відгуку (рис. 1). Якщо є взаємодія між факторами А \ В, то змі¬на фактора А викликає різноманітні зміни відгуку на різних рівнях фактора В. Таку взаємодію між рівнями і та j факторів А, В відповідно визначаємо як | ||
<br> | <br> | ||
| − | <math>\alpha _{ij}^{AB}={{\eta }_{ij}}-{{A}_{i}}-{{B}_{j}}+\mu ={{\eta }_{ij}}-{{\eta }_{i | + | <math>\alpha _{ij}^{AB}={{\eta }_{ij}}-{{A}_{i}}-{{B}_{j}}+\mu ={{\eta }_{ij}}-{{\eta }_{i}}-{{\eta }_{j}}+\eta .</math> (11) |
[[Файл:Gvf.png|378x159px|border|center|Графік впливів факторів]] | [[Файл:Gvf.png|378x159px|border|center|Графік впливів факторів]] | ||
| Рядок 119: | Рядок 119: | ||
<math>\alpha _{j}^{AB}=\alpha _{i}^{AB}.</math> | <math>\alpha _{j}^{AB}=\alpha _{i}^{AB}.</math> | ||
| + | Тоді загальна модель з урахуванням взаємодії двох факторів буде такою: | ||
| + | <math>M({{y}_{ijg}})={{\eta }_{ij}}=\mu +\alpha _{i}^{A}+\alpha _{j}^{B}+\alpha _{ij}^{AB}.</math> (12) | ||
| + | Верхні індекси позначають фактори, що взаємодіють між собою, а нижні - рівні, для яких визначається ефект. | ||
| + | Покажемо, що модель факторного експерименту с окремим випадком рівнян¬ня регресії. Для простоти будемо вважати, що немає взаємодії між факторами і повторень дослідів. Використовуючи вирази (1) і (9), отримаємо систему рівнянь | ||
| + | <math>\begin{align} | ||
| + | & {{y}_{11}}=\mu +\alpha _{1}^{A}+\alpha _{1}^{B}+{{e}_{11}}; \\ | ||
| + | & {{y}_{12}}=\mu +\alpha _{1}^{A}+\alpha _{2}^{B}+{{e}_{12}}; \\ | ||
| + | & ... \\ | ||
| + | & {{y}_{32}}=\mu +\alpha _{3}^{A}+\alpha _{3}^{B}+{{e}_{32}}; \\ | ||
| + | \end{align}</math> (13) | ||
| + | яку в матричному вигляді можна записати так: | ||
| + | <math>\overrightarrow{Y}=X\overrightarrow{\beta }+\overrightarrow{e},</math> (14) | ||
| + | де | ||
| + | |||
| + | |||
| + | <math>{{\overrightarrow{Y}}^{T}}=[{{y}_{11}},{{y}_{12}},...,{{y}_{32}}],</math> (15) | ||
| + | |||
| + | X- матриця причинних або незалежних (фіктивних) факторів: | ||
| + | |||
| + | |||
| + | <math>X=\left[ \begin{matrix} | ||
| + | 1 & 1 & 0 & 0 & 1 & 0 \\ | ||
| + | 1 & 1 & 0 & 0 & 0 & 1 \\ | ||
| + | 1 & 0 & 1 & 0 & 1 & 0 \\ | ||
| + | 1 & 0 & 1 & 0 & 0 & 1 \\ | ||
| + | 1 & 0 & 0 & 1 & 1 & 0 \\ | ||
| + | 1 & 0 & 0 & 1 & 0 & 1 \\ | ||
| + | \end{matrix} \right],</math> (16) | ||
| + | |||
| + | де перший стовпчик - це значення µ, другий, третій і четвертий – αAi п'ятий і шостий - αβi, і = 1, 2, 3; j = 1, 2; - вектор ефектів або параметрів. Транспонований вектор | ||
| + | |||
| + | <math>{{\overrightarrow{\beta }}^{T}}=[\mu ,\alpha _{1}^{A},\alpha _{2}^{A},\alpha _{3}^{A},\alpha _{1}^{B},\alpha _{2}^{B}].</math> (17) | ||
| + | |||
| + | Вектор помилок: | ||
| + | |||
| + | <math>{{\overrightarrow{e}}^{T}}=[{{e}_{11}},{{e}_{12}},...,{{e}_{32}}].</math> (18) | ||
| + | |||
| + | На основі виразів (6) і (8) отримаємо двосторонні умови: | ||
| + | |||
| + | <math>\alpha _{1}^{A}+\alpha _{2}^{A}+\alpha _{3}^{A}=0;</math>(19) | ||
| + | |||
| + | <math>\alpha _{1}^{B}+\alpha _{2}^{B}=0.</math> (20) | ||
| + | |||
| + | Обмеження (19) і (20) разом із так званими нормальними рівняннями вигляду | ||
| + | |||
| + | |||
| + | <math>{{X}^{T}}\overrightarrow{Y}={{X}^{T}}X\overrightarrow{\beta }</math> (21) | ||
| + | |||
| + | дають лише одні оцінки МНК. З регресійного аналізу відомо, що у разі справедливості виразу (11) ці оцінки одночасно будуть і оцінками максимальної правдоподібності, а також лінійними незміщеними оцінками з мінімальними значеннями дисперсії. | ||
| + | Таким чином, моделі факторних планів - це окремий випадок загальної лінійної регресійної моделі Вектор параметрів β містить сумарне середнє, головні ефекти і взаємодії; матриця незалежних змінних X складається лише з двох значень – 0 і 1 (використовують також позначення +1 та-1. або просто символи «+» і «-»). Отже, планування експерименту означає, що X вибирається таким чином, щоб оцінки мали деякі бажані властивості. | ||
| − | |||
=Факторний план 2k= | =Факторний план 2k= | ||
| + | |||
| + | Повний факторний експеримент передбачає реалізацію всіх можливих комбінацій рівнів факторів. У найпростішому випадку значення факторів задають на двох рівнях. За наявності к факторів, загальна кількість комбінацій буде 2k. | ||
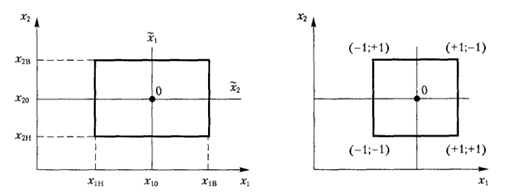
| + | Розглянемо графічну інтерпретацію факторного експерименту (рис.2). Вважатимемо, що нижньому рівню фактора відповідає значення -1. верхньому +1, а основному – 0. Виконати подібне перетворення можна так: | ||
| + | |||
| + | <math>{{\widetilde{x}}_{i}}=\frac{({{x}_{i}}-{{x}_{i0}})}{\vartriangle x},i=\overline{1,k}.</math> | ||
| + | |||
| + | [[Файл:P2.png|508x193px|border|center|Графічне зображення плану 22]] | ||
| + | |||
| + | <center>Рис.1 - Графічне зображення плану 22</center> | ||
| + | |||
| + | Розглянемо результати проведення експериментів, зведені в табл. 2. | ||
| + | |||
| + | Таблиця 2. План дворівневого факторного експерименту | ||
| + | |||
| + | <table border="0" cellspacing="0" cellpadding="0"> | ||
| + | <tr> | ||
| + | <td width="71" rowspan="2" valign="top"><p align="center"><strong>Фактор А</strong><strong> </strong></p></td> | ||
| + | <td colspan="2" valign="top"><p align="center"><strong>Фактор В</strong><strong> </strong></p></td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td width="67" valign="top"><p align="center"><strong>Рівень </strong><strong>1</strong></p></td> | ||
| + | <td width="91" valign="top"><p align="center"><strong> Рівень </strong><strong>2</strong></p></td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td width="71" valign="top"><p align="center"><strong> </strong><strong>Рівень </strong><strong>1</strong></p></td> | ||
| + | <td width="67" valign="top"><p align="center">y111<br /> | ||
| + | y112</p></td> | ||
| + | <td width="91" valign="top"><p align="center">y121<br /> | ||
| + | y122</p></td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td width="71" valign="top"><p align="center"><strong> </strong><strong>Рівень </strong><strong>2</strong></p></td> | ||
| + | <td width="67" valign="top"><p align="center"> Y211<br /> | ||
| + | y212</p></td> | ||
| + | <td width="91" valign="top"><p align="center"> y221<br /> | ||
| + | y222 </p></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | На основі даних табл. 2 можна записати таку систему рівнянь: | ||
| + | |||
| + | <math>\begin{align} | ||
| + | & {{y}_{11}}=\mu +\alpha _{1}^{A}+\alpha _{1}^{B}+\alpha _{11}^{AB}+{{e}_{11}}; \\ | ||
| + | & {{y}_{12}}=\mu +\alpha _{1}^{A}+\alpha _{2}^{B}+\alpha _{12}^{AB}+{{e}_{12}}; \\ | ||
| + | & {{y}_{21}}=\mu +\alpha _{2}^{A}+\alpha _{1}^{B}+\alpha _{21}^{AB}+{{e}_{21}}; \\ | ||
| + | & {{y}_{22}}=\mu +\alpha _{2}^{A}+\alpha _{2}^{B}+\alpha _{22}^{AB}+{{e}_{22}}; \\ | ||
| + | \end{align}</math> (22) | ||
| + | |||
| + | Оцінки параметрів моделі (22) за МНК можна знайти з урахуванням додаткових умов, які випливають із виразів (6), (8) і (11). Тоді отримаємо: | ||
| + | |||
| + | <math>\alpha _{1}^{A}=\alpha _{2}^{A};</math> (23) | ||
| + | |||
| + | <math>\alpha _{1}^{A}=\alpha _{2}^{A};</math> (24) | ||
| + | |||
| + | <math>\alpha _{21}^{AB}=\alpha _{11}^{AB};</math> (25) | ||
| + | |||
| + | <math>\alpha _{21}^{AB}=\alpha _{11}^{AB};</math>(26) | ||
| + | |||
| + | <math>\alpha _{22}^{AB}=-\alpha _{21}^{AB}=\alpha _{11}^{AB};</math> (27) | ||
| + | |||
| + | Підставивши вирази (23)-(27) у вираз (22), отримаємо систему рівнянь: | ||
| + | |||
| + | |||
| + | <math>\begin{align} | ||
| + | & {{y}_{11}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{11}}; \\ | ||
| + | & {{y}_{12}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{12}}; \\ | ||
| + | & {{y}_{21}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{21}}; \\ | ||
| + | & {{y}_{22}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{22}}; \\ | ||
| + | \end{align}</math> (28) | ||
| + | |||
| + | Запишемо систему рівнянь (28) у матричному вигляді | ||
| + | |||
| + | |||
| + | <math>\overrightarrow{Y}=X\overrightarrow{\beta }+\overrightarrow{e,}</math> (29) | ||
| + | |||
| + | <math>{{\overrightarrow{Y}}^{T}}=({{y}_{11}},{{y}_{12}},{{y}_{21}},{{y}_{22}}),</math> (30) | ||
| + | |||
| + | <math>X=\left[ \begin{matrix} | ||
| + | +1 & -1 & -1 & +1 \\ | ||
| + | +1 & -1 & +1 & -1 \\ | ||
| + | +1 & +1 & -1 & -1 \\ | ||
| + | +1 & +1 & +1 & +1 \\ | ||
| + | \end{matrix} \right],</math> (31) | ||
| + | |||
| + | |||
| + | <math>{{\overrightarrow{\beta }}^{T}}=(\mu ,\alpha _{2}^{A},\alpha _{2}^{B},\alpha _{11}^{AB}),</math> (32) | ||
| + | |||
| + | <math>{{\overrightarrow{e}}^{T}}=({{e}_{11}},{{e}_{12}},{{e}_{21}},{{e}_{22}}).</math> (33) | ||
| + | |||
| + | Зауважимо, що стовпчики матриці X - ортогональні, тобто | ||
| + | |||
| + | (34) | ||
| + | |||
| + | де і ) - будь-які два стовпчики матриці X. Очевидно, що X - невироджена матриця. Отже, оцінки МНК вектора такі: (35) | ||
| + | З виразу (34) і за умови, що | ||
| + | |||
| + | |||
| + | <math>\overrightarrow{x}_{i}^{T}{{\overrightarrow{x}}_{j}}=0,(i\ne j),</math> (36) | ||
| + | |||
| + | де N - число дослідів (у нашому випадку N = 4), отримаємо | ||
| + | |||
| + | (37) | ||
| + | |||
| + | де І - одинична матриця. | ||
| + | Тоді деякий h-й елемент ХT визначається як | ||
| + | |||
| + | (38) | ||
| + | |||
| + | де Xgh – g-й елемент вектора ; Н - загальне число параметрів (у даному випадку чотири). Підставимо вирази (37) і (38) у вираз (35). Тоді | ||
| + | |||
| + | (39) | ||
| + | |||
| + | Звідси | ||
| + | |||
| + | (41) | ||
| + | |||
| + | Порівняємо вираз (41) з визначенням головного ефекту : | ||
| + | |||
| + | (42) | ||
| + | |||
| + | Як бачимо, оцінка головного ефекту співпадає зі значенням самого ефекту. Таким самим способом можна показати, що оцінки за МНК головного ефекту і ефекту взаємодії утворюються просто за аналогією з їхніми визначеннями (7) і (11). | ||
| + | Зверніть увагу, в матриці X перший стовпчик стосується тільки сумарного середнього ц і містить лише одиниці зі знаком плюс. Другий та третій стовпчики відповідають головним ефектам і факторів А і В відповідно. Елемент g (g= ) цих стовпчиків приймає значення – 1, якщо фактор знаходиться на | ||
| + | нижньому рівні, та +1 на верхньому рівні. Для якісних факторів нижній і верх¬ній рівні є лише мнемонічними символами. | ||
| + | Четвертий стовпчик матриці X показує результат взаємодії двох факторів . Елементи цього стовпчика - добуток елементів другого і третього стовпчиків Тоді регресій ну модель можна записати як | ||
| + | |||
| + | (43) | ||
| + | |||
| + | де dgs, – -1. якщо фактор S в g-му досліді приймає значення нижнього рівня і dg, – +1 – у протилежному випадку. β0- загальне середнє µ; βs – головний ефект S-го фактора (наприклад, ); β12 ефект взаємодії двох факторів () | ||
| + | Рівняння (43) - це повний поліном другого степеня без квадратичних членів (немає членів ). | ||
| + | |||
| + | |||
=Дробовий дворівневий факторний експеримент= | =Дробовий дворівневий факторний експеримент= | ||
Версія за 19:59, 24 лютого 2010
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
Експеримент, в якому реалізуються всі можливі сполучення рівнів факторів, називається повним факторним експериментом.
http://elartu.tstu.edu.ua Презентація доповіді (університетський репозиторій).
Особливості планування експериментів
Опишемо послідовність Дій, які необхідно виконувати під час планування експериментів.
- Визначення відгуків (вихідних змінних) системи.
- Визначення факторів, які впливають на відгук системи. Більшість систем підпорядковуються принципу Парето - з огляду на характеристики системи істотними є лише деякі з множини факторів. У більшості систем 20 % факторів визначають 80 % властивостей системи.
- Визначення рівнів факторів. Мінімальна кількість рівнів для кожного фактора два - нижня і верхня межі значення фактора. У разі використання цього числа рівнів можна визначити тільки лінійні ефекти. Для врахування квадратичних ефектів необхідно використовувати три рівні, для кубічних ефектів - чотири і т. д Аналіз значно спрощується, якщо брати тільки рівновіддалені одне від одного значення рівнів. У цьому випадку маємо так зване ортогональне планування, або ортогональний експеримент.
Для множинних експериментів з чистом факторів більше одного дисперсійний аналіз передбачає використання для заключного аналізу ортогонального експерименту. Це означає, що оцінки відгуків у межах аналізу мають бути некорельованими. На практиці ортогональність гарантує використання тих самих випадкових послідовностей чисел під час виконання експериментів у межах кожної комбінації рівнів обробки.
Повний факторний експеримент
Експеримент, в якому реалізуються всі можливі сполучення рівнів факторів, називається повним факторним експериментом. Розглянемо простий двофакторний експеримент з одним фактором на двох рівнях, одним фактором на трьох рівнях і з двома спостереженнями в кожному досліді, тобто план 3x2 Запишемо в табл. 1 матрицю експерименту.
Таблиця 1. Матриця двофакторного експерименту
Фактор А |
Фактор В |
|
Рівень 1 |
Рівень 2 |
|
Рівень 1 |
y111 |
y121 |
Рівень 2 |
Y211 |
y221 |
Рівень 3 |
y311 |
y321 |
У загальному випадку: значення фактора yijg, де g - номер спостереження, і та j - номери рівнів факторів А та В відповідно. Нехай математичне сподівання вихідної змінної М(уijg) – nij Тоді очікувану функцію відгуку можна записати у такому вигляді:
[math]{{y}_{ijg}}={{\eta }_{ij}}+{{e}_{ijg}},i=\overline{1,I};j=\overline{1,J};g=1,2,3,...,[/math] (1)
де eijg, - похибка досліду (або шум), яка вважається незалежною нормально розподіленою випадковою величиною з математичним сподіванням нуль і диспер¬сією σ2, або
[math]{{e}_{ijg}}=HHP(0,{{\sigma }^{2}}).[/math] (2)
Покажемо, що моделі для планування експериментів є окремими випадками моделей лінійної регресії [21]. Знайдою середнє за всіма дослідами:
[math]\mu =\frac{\sum\limits_{i\in I}^{{}}{{}}\sum\limits_{i\in I}^{{}}{{{\eta }_{ij}}}}{IJ}=\eta,[/math] (3)
де крапка означає усереднення по всіх значеннях відповідного індексу.
Якщо знайти середнє значення відгуку для фактора А на рівні і з усіма рівнями фактора В, то
[math]{{A}_{i}}=\frac{\sum\limits_{j\in J}^{{}}{{{\eta }_{ij}}}}{J}={{\eta }_{i\bullet }}.[/math](4)
Тоді αAi, - головний ефект фактора А на рівні і визначається як різниця між його середнім і загальним середнім:
[math]\alpha _{i}^{A}={{A}_{i}}-\mu ={{\eta }_{j}}-\eta .[/math] (5)
З виразів (3)-(5) видно, що середнє головного ефекту дорівнює нулю, тому що
[math]\sum\limits_{i=1}^{I}{\alpha _{i}^{A}=\frac{1}{J}\sum\limits_{i}{\sum\limits_{j}{{{\eta }_{ij}}-\sum\limits_{i}{\mu =I\mu -I\mu =0}}}}.[/math] (6)
Головний ефект фактора В на рівні j визначаємо як
[math]\alpha _{j}^{B}={{B}_{j}}-\mu =\frac{1}{I}\sum\limits_{i}{{{\eta }_{ij}}-\mu =\eta -\eta.}[/math] (7)
Аналогічно
[math]\sum\limits_{j=1}^{J}{\alpha _{j}^{\beta }=0.}[/math] (8)
Якщо припустити, що фактори не взаємодіють між собою, то одержимо таку модель для планування проведення експерименту:
[math]M({{y}_{ijg}})={{\eta }_{ij}}=\mu +\alpha _{i}^{A}+\alpha _{j}^{B}.[/math] (9)
З виразу (9) маємо
[math]{{\eta }_{i1}}-{{\eta }_{i2}}=\alpha _{1}^{B}-\alpha _{2}^{B}.[/math] (10)
Вираз (10) є вірним для всіх рівнів і фактора А.
Відобразивши графічно, як фактор А впливає на рівень і фактора В, одержимо паралельні криві відгуку (рис. 1). Якщо є взаємодія між факторами А \ В, то змі¬на фактора А викликає різноманітні зміни відгуку на різних рівнях фактора В. Таку взаємодію між рівнями і та j факторів А, В відповідно визначаємо як
[math]\alpha _{ij}^{AB}={{\eta }_{ij}}-{{A}_{i}}-{{B}_{j}}+\mu ={{\eta }_{ij}}-{{\eta }_{i}}-{{\eta }_{j}}+\eta .[/math] (11)
Аналогічно, як було у виразах (6) і (8), маємо:
[math]\alpha _{j}^{AB}=\alpha _{i}^{AB}.[/math]
Тоді загальна модель з урахуванням взаємодії двох факторів буде такою:
[math]M({{y}_{ijg}})={{\eta }_{ij}}=\mu +\alpha _{i}^{A}+\alpha _{j}^{B}+\alpha _{ij}^{AB}.[/math] (12)
Верхні індекси позначають фактори, що взаємодіють між собою, а нижні - рівні, для яких визначається ефект. Покажемо, що модель факторного експерименту с окремим випадком рівнян¬ня регресії. Для простоти будемо вважати, що немає взаємодії між факторами і повторень дослідів. Використовуючи вирази (1) і (9), отримаємо систему рівнянь
[math]\begin{align} & {{y}_{11}}=\mu +\alpha _{1}^{A}+\alpha _{1}^{B}+{{e}_{11}}; \\ & {{y}_{12}}=\mu +\alpha _{1}^{A}+\alpha _{2}^{B}+{{e}_{12}}; \\ & ... \\ & {{y}_{32}}=\mu +\alpha _{3}^{A}+\alpha _{3}^{B}+{{e}_{32}}; \\ \end{align}[/math] (13)
яку в матричному вигляді можна записати так:
[math]\overrightarrow{Y}=X\overrightarrow{\beta }+\overrightarrow{e},[/math] (14)
де
[math]{{\overrightarrow{Y}}^{T}}=[{{y}_{11}},{{y}_{12}},...,{{y}_{32}}],[/math] (15)
X- матриця причинних або незалежних (фіктивних) факторів:
[math]X=\left[ \begin{matrix}
1 & 1 & 0 & 0 & 1 & 0 \\
1 & 1 & 0 & 0 & 0 & 1 \\
1 & 0 & 1 & 0 & 1 & 0 \\
1 & 0 & 1 & 0 & 0 & 1 \\
1 & 0 & 0 & 1 & 1 & 0 \\
1 & 0 & 0 & 1 & 0 & 1 \\
\end{matrix} \right],[/math] (16)
де перший стовпчик - це значення µ, другий, третій і четвертий – αAi п'ятий і шостий - αβi, і = 1, 2, 3; j = 1, 2; - вектор ефектів або параметрів. Транспонований вектор
[math]{{\overrightarrow{\beta }}^{T}}=[\mu ,\alpha _{1}^{A},\alpha _{2}^{A},\alpha _{3}^{A},\alpha _{1}^{B},\alpha _{2}^{B}].[/math] (17)
Вектор помилок:
[math]{{\overrightarrow{e}}^{T}}=[{{e}_{11}},{{e}_{12}},...,{{e}_{32}}].[/math] (18)
На основі виразів (6) і (8) отримаємо двосторонні умови:
[math]\alpha _{1}^{A}+\alpha _{2}^{A}+\alpha _{3}^{A}=0;[/math](19)
[math]\alpha _{1}^{B}+\alpha _{2}^{B}=0.[/math] (20)
Обмеження (19) і (20) разом із так званими нормальними рівняннями вигляду
[math]{{X}^{T}}\overrightarrow{Y}={{X}^{T}}X\overrightarrow{\beta }[/math] (21)
дають лише одні оцінки МНК. З регресійного аналізу відомо, що у разі справедливості виразу (11) ці оцінки одночасно будуть і оцінками максимальної правдоподібності, а також лінійними незміщеними оцінками з мінімальними значеннями дисперсії. Таким чином, моделі факторних планів - це окремий випадок загальної лінійної регресійної моделі Вектор параметрів β містить сумарне середнє, головні ефекти і взаємодії; матриця незалежних змінних X складається лише з двох значень – 0 і 1 (використовують також позначення +1 та-1. або просто символи «+» і «-»). Отже, планування експерименту означає, що X вибирається таким чином, щоб оцінки мали деякі бажані властивості.
Факторний план 2k
Повний факторний експеримент передбачає реалізацію всіх можливих комбінацій рівнів факторів. У найпростішому випадку значення факторів задають на двох рівнях. За наявності к факторів, загальна кількість комбінацій буде 2k. Розглянемо графічну інтерпретацію факторного експерименту (рис.2). Вважатимемо, що нижньому рівню фактора відповідає значення -1. верхньому +1, а основному – 0. Виконати подібне перетворення можна так:
[math]{{\widetilde{x}}_{i}}=\frac{({{x}_{i}}-{{x}_{i0}})}{\vartriangle x},i=\overline{1,k}.[/math]
Розглянемо результати проведення експериментів, зведені в табл. 2.
Таблиця 2. План дворівневого факторного експерименту
Фактор А |
Фактор В |
|
Рівень 1 |
Рівень 2 |
|
Рівень 1 |
y111 |
y121 |
Рівень 2 |
Y211 |
y221 |
На основі даних табл. 2 можна записати таку систему рівнянь:
[math]\begin{align} & {{y}_{11}}=\mu +\alpha _{1}^{A}+\alpha _{1}^{B}+\alpha _{11}^{AB}+{{e}_{11}}; \\ & {{y}_{12}}=\mu +\alpha _{1}^{A}+\alpha _{2}^{B}+\alpha _{12}^{AB}+{{e}_{12}}; \\ & {{y}_{21}}=\mu +\alpha _{2}^{A}+\alpha _{1}^{B}+\alpha _{21}^{AB}+{{e}_{21}}; \\ & {{y}_{22}}=\mu +\alpha _{2}^{A}+\alpha _{2}^{B}+\alpha _{22}^{AB}+{{e}_{22}}; \\ \end{align}[/math] (22)
Оцінки параметрів моделі (22) за МНК можна знайти з урахуванням додаткових умов, які випливають із виразів (6), (8) і (11). Тоді отримаємо:
[math]\alpha _{1}^{A}=\alpha _{2}^{A};[/math] (23)
[math]\alpha _{1}^{A}=\alpha _{2}^{A};[/math] (24)
[math]\alpha _{21}^{AB}=\alpha _{11}^{AB};[/math] (25)
[math]\alpha _{21}^{AB}=\alpha _{11}^{AB};[/math](26)
[math]\alpha _{22}^{AB}=-\alpha _{21}^{AB}=\alpha _{11}^{AB};[/math] (27)
Підставивши вирази (23)-(27) у вираз (22), отримаємо систему рівнянь:
[math]\begin{align}
& {{y}_{11}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{11}}; \\
& {{y}_{12}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{12}}; \\
& {{y}_{21}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{21}}; \\
& {{y}_{22}}=\mu -\alpha _{2}^{A}-\alpha _{2}^{B}-\alpha _{11}^{AB}+{{e}_{22}}; \\
\end{align}[/math] (28)
Запишемо систему рівнянь (28) у матричному вигляді
[math]\overrightarrow{Y}=X\overrightarrow{\beta }+\overrightarrow{e,}[/math] (29)
[math]{{\overrightarrow{Y}}^{T}}=({{y}_{11}},{{y}_{12}},{{y}_{21}},{{y}_{22}}),[/math] (30)
[math]X=\left[ \begin{matrix} +1 & -1 & -1 & +1 \\ +1 & -1 & +1 & -1 \\ +1 & +1 & -1 & -1 \\ +1 & +1 & +1 & +1 \\ \end{matrix} \right],[/math] (31)
[math]{{\overrightarrow{\beta }}^{T}}=(\mu ,\alpha _{2}^{A},\alpha _{2}^{B},\alpha _{11}^{AB}),[/math] (32)
[math]{{\overrightarrow{e}}^{T}}=({{e}_{11}},{{e}_{12}},{{e}_{21}},{{e}_{22}}).[/math] (33)
Зауважимо, що стовпчики матриці X - ортогональні, тобто
(34)
де і ) - будь-які два стовпчики матриці X. Очевидно, що X - невироджена матриця. Отже, оцінки МНК вектора такі: (35) З виразу (34) і за умови, що
[math]\overrightarrow{x}_{i}^{T}{{\overrightarrow{x}}_{j}}=0,(i\ne j),[/math] (36)
де N - число дослідів (у нашому випадку N = 4), отримаємо
(37)
де І - одинична матриця. Тоді деякий h-й елемент ХT визначається як
(38)
де Xgh – g-й елемент вектора ; Н - загальне число параметрів (у даному випадку чотири). Підставимо вирази (37) і (38) у вираз (35). Тоді
(39)
Звідси
(41)
Порівняємо вираз (41) з визначенням головного ефекту :
(42)
Як бачимо, оцінка головного ефекту співпадає зі значенням самого ефекту. Таким самим способом можна показати, що оцінки за МНК головного ефекту і ефекту взаємодії утворюються просто за аналогією з їхніми визначеннями (7) і (11). Зверніть увагу, в матриці X перший стовпчик стосується тільки сумарного середнього ц і містить лише одиниці зі знаком плюс. Другий та третій стовпчики відповідають головним ефектам і факторів А і В відповідно. Елемент g (g= ) цих стовпчиків приймає значення – 1, якщо фактор знаходиться на нижньому рівні, та +1 на верхньому рівні. Для якісних факторів нижній і верх¬ній рівні є лише мнемонічними символами. Четвертий стовпчик матриці X показує результат взаємодії двох факторів . Елементи цього стовпчика - добуток елементів другого і третього стовпчиків Тоді регресій ну модель можна записати як
(43)
де dgs, – -1. якщо фактор S в g-му досліді приймає значення нижнього рівня і dg, – +1 – у протилежному випадку. β0- загальне середнє µ; βs – головний ефект S-го фактора (наприклад, ); β12 ефект взаємодії двох факторів () Рівняння (43) - це повний поліном другого степеня без квадратичних членів (немає членів ).
Дробовий дворівневий факторний експеримент
Висновки
Список використаних джерел
- Моделювання систем - Томашевский В.М.:BHV, 2005. – 352с.
- Аністратенко В.О., Федоров В.Г. Математичне планування експерименту в АПК. К.: Вища школа, 1993. – 375 с.
- Теория эксперимента: Курс лекций. - А, В. Блохин. - Мн.: БГУ, 2002. - 67 с.

- Студент: Користувач:Залецький Михайло
- Виступ відбувся: 17 лютого 2010
- Тема: Регресійні моделі при повному 2 дробовому факторному експерименті. Визначення коефіцієнтів регресії