Відмінності між версіями «Параметр оптимізації»
Yulik (обговорення • внесок) (→2. Види параметрів оптимізації) |
Yulik (обговорення • внесок) м (→2. Види параметрів оптимізації) |
||
| Рядок 22: | Рядок 22: | ||
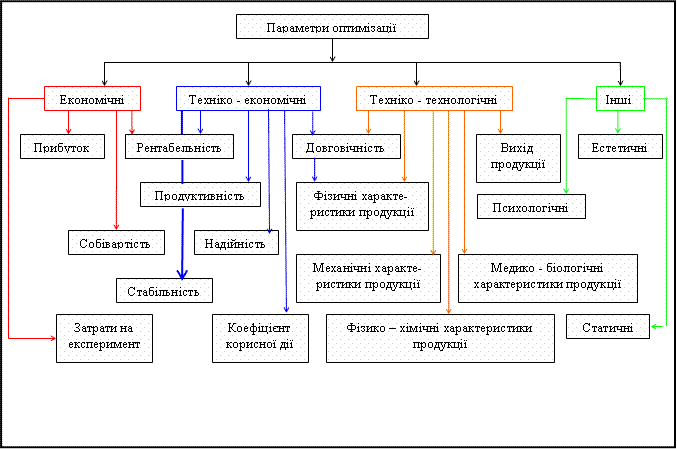
Дана класифікація не є повна і детальна вона відображає умовну схему, яка включає ряд практично важливих випадків. ''Основна мета даної класифікації'' - це допомога експериментаторові орієнтуватися в реальних ситуаціях. Реальні ситуації переважно складні. Вони часто вимагають одночасного обліку декількох, іноді дуже багатьох, параметрів. У принципі кожний об'єкт може характеризуватися відразу всією сукупністю параметрів, наведених на рисунку 1, або будь-якою підмножиною із цієї сукупності. Рух до оптимуму можливо, якщо обрано один-єдиний параметр оптимізації. Тоді інші характеристики процесу вже не виступають як параметри оптимізації, а служать обмеженнями. | Дана класифікація не є повна і детальна вона відображає умовну схему, яка включає ряд практично важливих випадків. ''Основна мета даної класифікації'' - це допомога експериментаторові орієнтуватися в реальних ситуаціях. Реальні ситуації переважно складні. Вони часто вимагають одночасного обліку декількох, іноді дуже багатьох, параметрів. У принципі кожний об'єкт може характеризуватися відразу всією сукупністю параметрів, наведених на рисунку 1, або будь-якою підмножиною із цієї сукупності. Рух до оптимуму можливо, якщо обрано один-єдиний параметр оптимізації. Тоді інші характеристики процесу вже не виступають як параметри оптимізації, а служать обмеженнями. | ||
| − | |||
[[Файл:Sxema.gif|border|center|Класифікація параметрів оптимізації]] | [[Файл:Sxema.gif|border|center|Класифікація параметрів оптимізації]] | ||
== 2.1 Економічні параметри== | == 2.1 Економічні параметри== | ||
Версія за 10:40, 22 лютого 2010
| |
Дана стаття являється неперевіреним навчальним завданням.
До вказаного терміну стаття не повинна редагуватися іншими учасниками проекту. Після завершення терміну виконання будь-який учасник може вільно редагувати дану статтю і витерти дане попередження, що вводиться за допомогою шаблону. |
.............. Презентація доповіді (університетський репозиторій).
Зміст
1. Параметр оптимізації
При плануванні екстремального експерименту важливо визначити параметр, який потрібно оптимізувати. Для цього ціль дослідження повинна бути сформульована чітко і допускати кількісну оцінку. Характеристика мети задана кількісно називається параметром оптимізації. Параметр оптимізації є реакцією (відгуком) на вплив факторів, які визначають поводження обраної системи. Реакція об'єкта багатогранна і багатоаспектна. Метою дослідження вибирають аспект, який представляє найбільший інтерес. Вибір оптимального рішення або порівняння двох альтернативних рішень проводиться за допомогою деякої залежної величини (функції), визначеної проектними параметрами. Ця величина називається цільовою функцією (або критерієм якості).
[math]u=f(x1,x2,...xn)[/math],
Задача оптимізації зводиться до відшукування таких значень параметрів, при яких цільова функція досягає максисусу або мінімуму. Для однозначності загальних міркувань важається оптимальним максимальне значення виходу.
Задачі оптимізації
Безумовні задачі оптимізації полягає у відшуканні максимуму або мінімуму дійсної функції від n дійсних змінних і визначення відповідних значень аргументів.
Умовні задачі оптимізації, або задачі з обмеженнями, — це такі, при формулюванні яких задаються деякі умови (обмеження) на безлічі.
2. Види параметрів оптимізації
Залежно від об'єкта і мети дослідження параметри оптимізації є дуже різноманітними. Щоб орієнтуватися в цьому різноманітті, вводять деяку класифікацію . Дана класифікація не є повна і детальна вона відображає умовну схему, яка включає ряд практично важливих випадків. Основна мета даної класифікації - це допомога експериментаторові орієнтуватися в реальних ситуаціях. Реальні ситуації переважно складні. Вони часто вимагають одночасного обліку декількох, іноді дуже багатьох, параметрів. У принципі кожний об'єкт може характеризуватися відразу всією сукупністю параметрів, наведених на рисунку 1, або будь-якою підмножиною із цієї сукупності. Рух до оптимуму можливо, якщо обрано один-єдиний параметр оптимізації. Тоді інші характеристики процесу вже не виступають як параметри оптимізації, а служать обмеженнями.
2.1 Економічні параметри
Економічні параметри оптимізації, такі, як прибуток, собівартість і рентабельність, звичайно використаються при дослідженні діючих промислових об'єктів, тоді як витрати на експеримент має сенс оцінювати в будь-яких дослідженнях, у тому числі і лабораторних. Якщо ціна досвідів однакова, витрати на експеримент пропорційні числу досвідів, які необхідно поставити для рішення даного завдання. Це значною мірою визначає вибір плану експерименту.
2.2 Техніко –екопомічні параметри
Серед техніко-економічних параметрів найбільше поширення має продуктивність. Такі параметри, як довговічність, надійність і стабільність, пов'язані із тривалими спостереженнями. Є деякий досвід їхнього використання при вивченні дорогих відповідальних об'єктів, наприклад радіоелектронних апаратур.
2.3 Техніко – технологічні параметри
Майже у всіх дослідженнях доводиться враховувати кількість і якість одержуваного продукту. Як міру кількості продукту використають вихід, наприклад, відсоток виходу хімічної реакції, вихід придатних виробів. Показники якості надзвичайно різноманітні. У представленій класифікації вони згруповані по видах властивостей. Характеристики кількості і якості продукту утворять групу техніко-технологічних параметрів.
2.4 Інші параметри
Під рубрикою "інші" згруповані різні параметри, які рідше зустрічаються, але не є менш важливими. Сюди потрапили статистичні параметри, використовувані для поліпшення характеристик випадкових величин або випадкових функцій. Прикладам таких параметрів будуть завдання на мінімізацію дисперсії випадкової величини, на зменшення числа викидів випадкового процесу за фіксований рівень і т.д. Останнє завдання виникає, зокрема , при виборі оптимальних настроювань автоматичних регуляторів або при поліпшенні властивостей ниток (дріт, пряжа, штучне волокно й ін.).
З ростом складності об'єкта зростає роль психологічних аспектів взаємодії людини або тварини з об'єктом. Наприклад при виборі оптимальної організації робочого місця оператора параметром оптимізації може служити число помилкових дій у різних можливих ситуаціях.
При рішенні завдання технічної естетики або порівнянні творів мистецтва виникає потреба в естетичних параметрах. Вони засновані на ранговому підході.
3. Приклад вибору параметра оптимізації
Приклад 1. Під час другої світової війни кілька сотень англійських торговельних суден були озброєні зенітними знаряддями для захисту від ворожих бомбардувальників. Оскільки цей захід було досить дорогим (було потрібно мати на кожному судні бойову команду), через кілька місяців вирішили оцінити його ефективність. Який з параметрів оптимізації більше підходить для цієї мети?
Число збитих літаків. Втрати в суднах, оснащених знаряддями, у порівнянні із суднами без знарядь. Якщо вважати, що ефективність установлення знарядь на торговельні судна можна оцінити числом збитих літаків, то буде очевидно, що значення параметра оптимізації в цьому випадку будуть низькими, тому що існують куди більше ефективні засоби для цієї мети (авіація, бойовий флот), чим зенітні знаряддя на торговельних .
Якщо вважати, що ефективність установки знарядь на торговельні судна можна оцінити зіставленням втрат у судах, оснащених знаряддями, із втратами в судах без знарядь, то це розумний вибір параметра оптимізації, тому що основним завданням при установці знарядь був захист суден. Літаки змушені були тепер використати протизенітні маневри і бомбардування з великої висоти, що зменшувало втрати.
Із числа атакованих літаками торговельних суден із зенітними знаряддями було потоплено 10% суден, а втрати в суднах без знарядь склали 25%. Витрати на установку знарядь і зміст бойових розрахунків окупилися дуже швидко.
4. Вимоги до параметрів оптимізації.
Параметр оптимізації - це ознака, по якій оптимізують процес. Він повинен бути кількісним, задаватися числом, його необхідно вимірювати при будь-якій можливій комбінації обраних рівнів факторів. Безліч значень, які може приймати параметр оптимізації називають областю його визначення. Області визначення можуть бути неперервними і дискретними, обмеженими і необмеженими.
Наприклад, вихід реакції - це параметр оптимізації з безперервною обмеженою областю визначення. Він може змінюватися в інтервалі від 0 до 100%. Число бракованих виробів, число зерен на шліфі сплаву, число кров'яних тілець у пробі крові - от приклади параметрів з дискретною областю визначення, обмеженої знизу.
Якщо немає способу кількісного виміру результату, то доводиться скористатися прийомом, який називається ранжируванням (ранговим підходом). При цьому параметрам оптимізації привласнюються оцінки - ранги по заздалегідь обраній шкалі: двобальної, п'ятибальної і т.д. Ранговий параметр має дискретну обмежену область визначення. У найпростішому випадку область містить два значення (так, ні; добре, погано). Ранг - це кількісна оцінка параметра оптимізації, але вона носить умовний (суб'єктивний) характер. Для кожного фізично вимірюваного параметра оптимізації можна побудувати ранговий аналог. Потреба в побудові такого аналога виникає, якщо наявні в розпорядженні дослідника чисельні характеристики неточні або невідомий спосіб побудови задовільних чисельних оцінок. За інших рівних умов завжди потрібно віддавати перевагу фізичному виміру, тому що ранговий підхід менш чутливий і з його допомогою важко вивчати тонкі ефекти.
Наступна вимога: параметр оптимізації повинен виражатися одним числом. Іноді це виходить природно, як реєстрація показання приладу. Наприклад, швидкість руху машини визначається числом на спідометрі. Частіше доводиться робити деякі обчислення. Так буває при розрахунку виходу реакції. У хімії часто потрібно одержувати продукт із заданим відношенням компонентів, наприклад, А : В = 3 : 2. Один з можливих варіантів рішення подібних завдань полягає в тому, щоб виразити відношення одним числом 1,5) і як параметр оптимізації користуватися значеннями відхилень (або квадратів відхилень) від цього числа.
Ще одна вимога, пов'язане з кількісною природою параметра оптимізації, - однозначність у статистичному змісті. Заданому набору значень факторів повинне відповідати одне, з точністю до помилки експерименту, значення параметра оптимізації.
Для успішного досягнення мети дослідження необхідно, щоб параметр оптимізації дійсно оцінював ефективність функціонування системи в заздалегідь обраному змісті. Ця вимога є головна, визначальна коректність постановки завдання.
Подання про ефективність не залишається постійним у ході дослідження. Воно міняється в міру нагромадження інформації і залежно від досягнутих результатів. Це приводить до послідовного підходу при виборі параметра оптимізації. Так, наприклад, на перших стадіях дослідження технологічних процесів як параметр оптимізації часто використається вихід продукту. Однак надалі , коли - можливість підвищення виходу вичерпана, нас починають цікавити такі параметри, як собівартість, чистота продукту і т.д..
Говорячи про оцінку ефективності функціонування системи, важливо пам'ятати, що мається на увазі систему в цілому. Часто система складається з ряду підсистем, кожна з яких може оцінюватися своїм локальним параметром оптимізації. При цьому оптимальність кожної з підсистем по своєму параметрі оптимізації не виключає можливості загибелі системи в цілому.
Параметр оптимізації не тільки повинен бути ефективним потрібно, щоб він був ефективний у статистичному змісті. Тобто ця вимога зводиться до вибору параметра оптимізації, що визначається з найбільшою можливою точністю.
Наступна вимога до параметра оптимізації - вимога універсальності або повноти. Під універсальністю параметра оптимізації розуміється його здатність всебічно характеризувати об'єкт. Технологічні параметри оптимізації недостатньо універсальні вони не враховують економіку. Універсальністю володіють узагальнені параметри оптимізації, які є функцією від декількох приватних параметрів.
Список використаних джерел
- http://window.edu.ru/window_catalog/files/r18438/Mtdukm8.pdf - Основи планування експаременту (Січень 2010);
- Аністратенко В. О., Федоров В. Г. Математичне планування експерементів в АПК. Київ: Вища школа, 1993.- 375 с.
- http://window.edu.ru/window_catalog/pdf2txt?p_id=1180&p_page=1 – Основи планування експериментів (Січень 2010);
- http://uk.wikipedia.org/wiki/Планування_експерименту – Планування експерименту (Січень 2010);

- Студент: Користувач:yulik
- Виступ відбувся: 21 лютий 2010
- Тема: Види параметрів оптимізації. Вимоги до факторів і параметрів оптимізації..