Відмінності між версіями «Динамічний тиск»
м |
м |
||
| Рядок 1: | Рядок 1: | ||
== Динамічний тиск == | == Динамічний тиск == | ||
| − | '''Динамічний тиск''' (іноді його називають '''тиском швидкості''') - це збільшення тиску рухомої рідини над її статичним значенням за рахунок руху. Таким чином, його можна розглядати як кінетичну енергію | + | '''Динамічний тиск''' (іноді його називають '''тиском швидкості''') - це збільшення тиску рухомої рідини над її статичним значенням за рахунок руху. Таким чином, його можна розглядати як кінетичну енергію одиниці об'єму рідини. В динаміці нестисливої і стисливої рідини, динамічний тиск ''q'' або ''Q'' визначається як: |
:<math>q = \dfrac {\rho\, u^{2}}{2}</math> | :<math>q = \dfrac {\rho\, u^{2}}{2}</math> | ||
де (використовуючи одиниці СІ): | де (використовуючи одиниці СІ): | ||
| Рядок 13: | Рядок 13: | ||
| <math>u\;</math> || = швидкість потоку в м/с. | | <math>u\;</math> || = швидкість потоку в м/с. | ||
|} | |} | ||
| − | Для | + | Для нестисливого потоку рідини, динамічний тиск рідини - це різниця між загальним і статичним тиском. З закону Бернуллі динамічний тиск надає |
:<math> p_0 -p_s = \dfrac {\rho\, u^{2}}{2}</math> | :<math> p_0 -p_s = \dfrac {\rho\, u^{2}}{2}</math> | ||
| − | де <math>p_0</math> and <math>p_s</math> - загальний і статичний тиски відповідно. | + | де <math>p_0</math> and <math>p_s</math> - загальний і статичний тиски, відповідно. |
__TOC__ | __TOC__ | ||
== Фізичне значення == | == Фізичне значення == | ||
| − | Динамічний тиск - кінетична енергія | + | Динамічний тиск - це кінетична енергія одиниці об'єму рідини. Динамічний тиск є одним із доданків у рівнянні Бернуллі, яке можна отримати із закону збереження механічної енергії для потоку рідини. У частковому випадку для окремої точки рідини динамічний тиск дорівнює різниці між повним тиском і статичним тиском. |
| − | Інший важливий аспект динамічного тиску полягає в тому, що, як показує | + | Інший важливий аспект динамічного тиску полягає в тому, що, як показує метод аналізу розмірностей, аеродинамічне напруження, яке зазнає повітряне судно, що рухається зі швидкістю <math>v</math> пропорційна густині повітря та квадрату <math>v</math>, тобто пропорційна <math>q</math>. |
| − | Тому, переглядаючи коливання <math>q</math> під час польоту, можна визначити, як буде змінюватися напруга, зокрема, коли | + | Тому, переглядаючи коливання <math>q</math> під час польоту, можна визначити, як буде змінюватися напруга, і зокрема, коли вона досягне свого максимального значення. Точку максимального аеродинамічного навантаження часто називають максимальною ''max Q'', і це важливий параметр у багатьох додатках, таких як ракети-носії. |
==Використання== | ==Використання== | ||
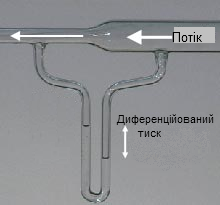
| − | [[Image:VenturiFlow.png|right|thumb|Потік повітря через | + | [[Image:VenturiFlow.png|right|thumb|Потік повітря через витратомір Вентурі, що показує стовпчики, з'єднані у U-подібній формі (манометр) і частково заповнені водою. Лічильник "зчитується" як перепад тиску в см або дюймах води і еквівалентний різниці швидкості головки.]] |
| − | Динамічний тиск, поряд зі статичним тиском і тиском внаслідок підвищення, використовується в принципі Бернуллі, як енергетичний баланс у закритій системі. Ці три терміни використовуються для визначення стану замкнутої системи | + | Динамічний тиск, поряд зі статичним тиском і тиском внаслідок підвищення, використовується в принципі Бернуллі, як енергетичний баланс у закритій системі. Ці три терміни використовуються для визначення стану замкнутої системи нестисливої рідини постійної щільності. |
| − | Коли динамічний тиск | + | Коли динамічний тиск поділено на густину рідини та прискорення, за рахунок сили тяжіння, результат називається швидкість напору. У витратомірі Вентурі, диференціал напору може бути використаний для обчислення швидкості напору, який є еквівалентними на сусідньому малюнку. Альтернативою швидкості напору є динамічна напір. |
| − | == | + | == Стисливий потік == |
| − | Багато авторів визначають ''динамічний тиск'' лише для | + | Багато авторів визначають ''динамічний тиск'' лише для нестисливих потоків. (Для стисливих потоків ці автори використовують поняття ударного тиску.) Однак, визначення ''динамічного тиску'' може бути розширене, якщо включити потоки стисливого тиску. |
| − | Якщо рідину, про яку йде мова, можна вважати ідеальним газом (як правило, це стосується повітря), динамічний тиск може бути виражений | + | Якщо рідину, про яку йде мова, можна вважати ідеальним газом (як правило, це стосується повітря), динамічний тиск може бути виражений, як залежність від тиску рідини та числа Маха. |
Застосовуючи закон ідеального газу: | Застосовуючи закон ідеального газу: | ||
| Рядок 78: | Рядок 78: | ||
== Посилання == | == Посилання == | ||
* https://en.wikipedia.org/wiki/Dynamic_pressure | * https://en.wikipedia.org/wiki/Dynamic_pressure | ||
| − | * | + | * L. J. Clancy (1975), ''Aerodynamics'', Pitman Publishing Limited, London. |
| − | * | + | * Houghton, E.L. and Carpenter, P.W. (1993), ''Aerodynamics for Engineering Students'', Butterworth and Heinemann, Oxford UK. |
Версія за 11:34, 9 грудня 2019
Динамічний тиск
Динамічний тиск (іноді його називають тиском швидкості) - це збільшення тиску рухомої рідини над її статичним значенням за рахунок руху. Таким чином, його можна розглядати як кінетичну енергію одиниці об'єму рідини. В динаміці нестисливої і стисливої рідини, динамічний тиск q або Q визначається як:
- [math]q = \dfrac {\rho\, u^{2}}{2}[/math]
де (використовуючи одиниці СІ):
[math]q\;[/math] = динамічний тиск у паскалях, [math]\rho\;[/math] = щільність рідини в кг/м3 (наприклад, густина води), [math]u\;[/math] = швидкість потоку в м/с.
Для нестисливого потоку рідини, динамічний тиск рідини - це різниця між загальним і статичним тиском. З закону Бернуллі динамічний тиск надає
- [math]p_0 -p_s = \dfrac {\rho\, u^{2}}{2}[/math]
де [math]p_0[/math] and [math]p_s[/math] - загальний і статичний тиски, відповідно.
Фізичне значення
Динамічний тиск - це кінетична енергія одиниці об'єму рідини. Динамічний тиск є одним із доданків у рівнянні Бернуллі, яке можна отримати із закону збереження механічної енергії для потоку рідини. У частковому випадку для окремої точки рідини динамічний тиск дорівнює різниці між повним тиском і статичним тиском.
Інший важливий аспект динамічного тиску полягає в тому, що, як показує метод аналізу розмірностей, аеродинамічне напруження, яке зазнає повітряне судно, що рухається зі швидкістю [math]v[/math] пропорційна густині повітря та квадрату [math]v[/math], тобто пропорційна [math]q[/math]. Тому, переглядаючи коливання [math]q[/math] під час польоту, можна визначити, як буде змінюватися напруга, і зокрема, коли вона досягне свого максимального значення. Точку максимального аеродинамічного навантаження часто називають максимальною max Q, і це важливий параметр у багатьох додатках, таких як ракети-носії.
Використання
Динамічний тиск, поряд зі статичним тиском і тиском внаслідок підвищення, використовується в принципі Бернуллі, як енергетичний баланс у закритій системі. Ці три терміни використовуються для визначення стану замкнутої системи нестисливої рідини постійної щільності.
Коли динамічний тиск поділено на густину рідини та прискорення, за рахунок сили тяжіння, результат називається швидкість напору. У витратомірі Вентурі, диференціал напору може бути використаний для обчислення швидкості напору, який є еквівалентними на сусідньому малюнку. Альтернативою швидкості напору є динамічна напір.
Стисливий потік
Багато авторів визначають динамічний тиск лише для нестисливих потоків. (Для стисливих потоків ці автори використовують поняття ударного тиску.) Однак, визначення динамічного тиску може бути розширене, якщо включити потоки стисливого тиску.
Якщо рідину, про яку йде мова, можна вважати ідеальним газом (як правило, це стосується повітря), динамічний тиск може бути виражений, як залежність від тиску рідини та числа Маха.
Застосовуючи закон ідеального газу:
- [math]p_s = \rho_m\, R\, T,\,[/math]
визначення швидкості звуку [math]a[/math] і числа Маха [math]M[/math]:
- [math]a = \sqrt{\gamma\, R\, T \over m_m},[/math]
- [math]M = \frac{u}{a},[/math]
і також [math]q = \tfrac12\, \rho\, u^2[/math], динамічний тиск можна переписати так:
- [math]q = \tfrac12\, \gamma\, p_{s}\, M^{2},[/math]
де (використовуючи одиниці СІ):
[math]p_{s}\;[/math] = статичний тиск у Паскалі, є також базовою одиницею тиску СІ [math]\rho_m\;[/math] = молярна щільність ідеального газу в моль/м3 [math]m_m\;[/math] = маса молю ідеального газу в кг/моль [math]\rho\ = \rho_m m_m\;[/math] = щільність ідеального газу в кг/м3 [math]R\;[/math] = константа газу (8,3144 Дж/(моль·К)), [math]T\;[/math] = абсолютна температура в кельвінах (К), [math]M\;[/math] = число Маха (безрозмірна), [math]\gamma\;[/math] = співвідношення питомих нагрівань (безвимірна) (1,4 для повітря в умовах моря), [math]u\;[/math] = швидкість потоку в м/с, [math]a\;[/math] = швидкість звуку в м/с
Посилання
- https://en.wikipedia.org/wiki/Dynamic_pressure
- L. J. Clancy (1975), Aerodynamics, Pitman Publishing Limited, London.
- Houghton, E.L. and Carpenter, P.W. (1993), Aerodynamics for Engineering Students, Butterworth and Heinemann, Oxford UK.