Відмінності між версіями «Реактивне сопло»
Taras (обговорення • внесок) (→Принцип дії) |
Taras (обговорення • внесок) (→Принцип дії) |
||
| Рядок 63: | Рядок 63: | ||
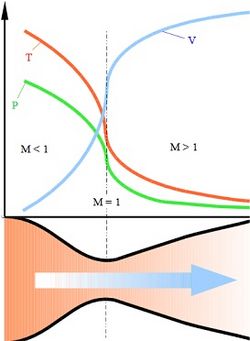
[[Файл:Nozzle de Laval diagram.jpg|thumb|right|250px|Ілюстрація роботи сопла Лаваля. По мірі руху газу по соплу, його абсолютна температура Т і тиск Р понижуються, а швидкість V збільшується. М — число Маха.]] | [[Файл:Nozzle de Laval diagram.jpg|thumb|right|250px|Ілюстрація роботи сопла Лаваля. По мірі руху газу по соплу, його абсолютна температура Т і тиск Р понижуються, а швидкість V збільшується. М — число Маха.]] | ||
'''З чого можна зробити наступні висновки:''' | '''З чого можна зробити наступні висновки:''' | ||
| + | |||
| + | |||
| + | * При '''дозвуковій швидкості''' рух газу <math>\,(M<1)</math>, похідна <math>\frac{dA}{dx}<0</math> ''' — сопло звужується'''. | ||
| + | * При '''надзвуковій швидкості''' рух газу <math>\,(M>1)</math>, похідна <math>\frac{dA}{dx}>0</math> ''' — сопло розширюється'''. | ||
| + | * При русі газу '''зі швидкістю звуку''' <math>\,(M = 1)</math>, похідна <math>\frac{dA}{dx}=0</math> — площа поперечного перерізу досягає '''екстремума''', тобто має місце '''найвужчий переріз''' сопла, яке називається '''критичним'''. | ||
Версія за 16:14, 24 листопада 2012
Сопло Лаваля - технічне пристосування, яке розганяє газовий потік до надзвукових швидкостей. Широко використовується на деяких типах парових турбін і є важливою частиною сучасних ракетних двигунів і надзвукових реактивних авіаційних двигунів. Сопло являє собою канал, звужений в середині. У простому випадку таке сопло може складатися з пари усічених конусів, сполучених вузькими кінцями. Ефективні сопла сучасних ракетних двигунів профілюються на підставі газодинамічних розрахунків. Пріоритет Годдарда на застосування сопла Лаваля для ракет підтверджується малюнком в описі винаходу в патенті США "US Patet 1102653" від 7 липня 1914 р., на двоступеневу твердопаливну ракету, заявленому в жовтні 1913 р. У Росії в ракетному двигуні сопло Лаваля вперше було використано генералом М. М. Поморцевим в 1915 р.. У листопаді 1915 року в Аеродинамічний інститут звернувся генерал М. М. Поморцев з проектом бойової пневматичної ракети. Ракета Поморцева приводилася в рух стисненим повітрям, що істотно обмежувало її дальність, але зате робило її безшумною. Ракета призначалася для стрільби з окопів по ворожих позиціях. Боєголовка оснащувалася тротилом. У ракеті Поморцева було застосовано два цікавих конструктивних рішення: в двигуні використовувалось сопло Лаваля, а з корпусом був зв'язаний кільцевий стабілізатор. У реактивному двигуні застосовують:
- звужуюче реактивне сопло для створення дозвукових швидкостей;
- звужуюче-розширяюче реактивне сопло (сопло Лаваля) - для отримання надзвукових швидкостей .
- косе сопло - для отримання надзвукових швидкостей при постійному профілі і широкому діапазоні робочих швидкостей.
Принцип дії
Феномен прискорення газу до надзвукових швидкостей в соплі Лаваля був виявлений в кінці XIX ст. експериментальним шляхом. Пізніше це явище знайшло теоретичне пояснення в рамках газової динаміки.
При наступному аналізі перебігу газу в соплі Лаваля приймаються наступні допущення:
- Газ вважається ідеальним.
- Газовий потік є ізоентропним (тобто має постійну ентропію, сили тертя і дисипативні втрати не враховуються) і адіабатичним (тобто теплота не підводиться і не відводиться).
- Газовий протік є стаціонарним і одновимірним, тобто в будь фіксованій точці сопла всі параметри потоку постійні в часі і змінюються тільки уздовж осі сопла, причому у всіх точках обраного поперечного перерізу параметри потоку однакові, а вектор швидкості газу всюди паралельний осі симетрії сопла.
- Масова витрата газу однакова у всіх поперечних перерізах потоку.
- Вплив всіх зовнішніх сил і полів (в тому числі гравітаційного) дуже мале.
- Вісь симетрії сопла є просторовою координатою [math]\, x[/math].
Відношення локальної швидкості [math]\,v[/math] до локальної швидкості звуку [math]\, C[/math] позначається числом Маха, яке також розуміється місцевим, тобто залежним від координати [math]\, x[/math]:
З рівняння стану ідеального газу:[math]\frac{dp}{d\rho}=C^2[/math], тут [math]\,\rho[/math] - локальна щільність газу, [math]\, p[/math] - локальне тиск. З урахуванням цього, а також з урахуванням стаціонарності і одномірності потоку рівняння Ейлера приймає вигляд:
якщо врхувати рівняння (1), то отримаємо:
Рівняння (2) є ключовим
Переглянемо його в наступній формі:
Велмчмнм [math]\frac{1}{\rho} \frac{d\rho}{dx}[/math] і [math]\frac{1}{v} \frac{dv}{dx}[/math] характеризують відносну ступінь змінності по координаті [math]\, x[/math] щільності газу і його швидкості відповідно. Причому рівняння (2.1) показує, що співвідношення між цими величинами дорівнює квадрату числа Маха (знак мінус означає протилежну спрямованість змін: при зростанні швидкості щільність зменшується). Таким чином, на дозвукових швидкостях [math]\, (M \lt 1)[/math] щільність змінюється у меншій мірі, ніж швидкість, а на надзвукових [math]\, (M\gt 1)[/math] - навпаки. Як буде видно далі, це і визначає звужуючо-розширюючу форму сопла.
Оскільки масовий розхід газу постіний:
где [math]\, A[/math] — площа поперечного перерізу сопла,
диференціюючи обидві частини цього рівняння по [math]\, x[/math], отримуємо:
Післяпідстановки з (2) в це рівняння, остаточно отримуємо:
При збільшенні швидкості газу в соплі знак фиразу [math]\frac{A}{v}\cdot\frac{dv}{dx}[/math] додатній і, знак похідниї [math]\frac{dA}{dx}[/math] визначається знаком виразу: [math]\,({M^2 - 1})[/math]
З чого можна зробити наступні висновки:
- При дозвуковій швидкості рух газу [math]\,(M\lt 1)[/math], похідна [math]\frac{dA}{dx}\lt 0[/math] — сопло звужується.
- При надзвуковій швидкості рух газу [math]\,(M\gt 1)[/math], похідна [math]\frac{dA}{dx}\gt 0[/math] — сопло розширюється.
- При русі газу зі швидкістю звуку [math]\,(M = 1)[/math], похідна [math]\frac{dA}{dx}=0[/math] — площа поперечного перерізу досягає екстремума, тобто має місце найвужчий переріз сопла, яке називається критичним.