Відмінності між версіями «Епюра гідростатичного тиску»
Bohdan (обговорення • внесок) |
Bohdan (обговорення • внесок) |
||
| Рядок 31: | Рядок 31: | ||
оскільки <math>h = ysin \alpha</math> | оскільки <math>h = ysin \alpha</math> | ||
Проінтегруємо одержаний вираз, врахувавши заміну<math> y=\rho g</math> | Проінтегруємо одержаний вираз, врахувавши заміну<math> y=\rho g</math> | ||
| − | + | <math>F=\int_{\omega}d\omega +ysin\alpha \int_{\omega}yd\omega</math> | |
де <math>\int_{\omega}d\omega =\omega </math>, a <math>int_{\omega}yd\omega </math>- є статистичний момент <math>S_{x}</math> ділянки, площею <math>\omega</math> відносно осі x-ів (А-А’) | де <math>\int_{\omega}d\omega =\omega </math>, a <math>int_{\omega}yd\omega </math>- є статистичний момент <math>S_{x}</math> ділянки, площею <math>\omega</math> відносно осі x-ів (А-А’) | ||
Оскільки - <math>\int_{\omega}yd\omega =S_{x}=y_{c}\omega</math> , то | Оскільки - <math>\int_{\omega}yd\omega =S_{x}=y_{c}\omega</math> , то | ||
| Рядок 41: | Рядок 41: | ||
Результуюча сила (<math>P_{nadl.}=\rho gh_{c}\omega </math>) надлишкового тиску не прикладена до центру поверхні стінки, оскільки надлишковий тиск змінний з глибиною. Координату точки прикладання рівнодійної сили надлишкового тиску можна знайти з рівняння моментів сил відносно осі x-ів. Тоді | Результуюча сила (<math>P_{nadl.}=\rho gh_{c}\omega </math>) надлишкового тиску не прикладена до центру поверхні стінки, оскільки надлишковий тиск змінний з глибиною. Координату точки прикладання рівнодійної сили надлишкового тиску можна знайти з рівняння моментів сил відносно осі x-ів. Тоді | ||
<math>F_{nadl.}\cdot y_{D}=\int_{\omega}\rho ghyd\omega</math> | <math>F_{nadl.}\cdot y_{D}=\int_{\omega}\rho ghyd\omega</math> | ||
| − | Але <math>h=ysin\alpha</math> , тому <math>F_{nadl.}\cdot y_{D}=\rho gsin\alpha \int_{\omega}y^{2}d\omega</math> | + | Але <math>h=ysin\alpha</math> , тому <math>F_{nadl.}\cdot y_{D}=\rho gsin\alpha \int_{\omega}y^{2}d\omega</math>(2.2) |
| − | |||
де<math>\int_{\omega}y^{2}d\omega</math> - момент інерції <math>J_{x}</math> поверхні, на яку тисне рідина відносно осі x-ів. | де<math>\int_{\omega}y^{2}d\omega</math> - момент інерції <math>J_{x}</math> поверхні, на яку тисне рідина відносно осі x-ів. | ||
| − | З (2.2) отримуємо<math>y_{D}=\frac{\rho gsin\alpha J_{x}}{\rho gh_{c}\omega}=\frac{sin\alpha J_{x}}{y_{c}sin\alpha\omega}=\frac{J_{x}}{y_{c}\omega}</math> | + | З (2.2) отримуємо<math>y_{D}=\frac{\rho gsin\alpha J_{x}}{\rho gh_{c}\omega}=\frac{sin\alpha J_{x}}{y_{c}sin\alpha\omega}=\frac{J_{x}}{y_{c}\omega}</math>(2.3) |
| − | |||
Замінимо момент інерції відносно осі x-ів на момент відносно осі, що проходить через центр ваги поверхні : | Замінимо момент інерції відносно осі x-ів на момент відносно осі, що проходить через центр ваги поверхні : | ||
<math>J_{x}=y_{c}^{2}\omega+J_{c}</math> | <math>J_{x}=y_{c}^{2}\omega+J_{c}</math> | ||
Версія за 18:37, 12 травня 2012
Епюра гідростатичного тиску (рос.эпюра гидростатического давления; англ. hydrostatic pressure profile (diagram); нім. Figur f des hydrostatischen Druckes) — графік, який побудовано для плоскої прямокутної фігури вертикальної або похилої «стінки», що піддається гідростатичному тиску, і визначає розподіл гідростатичного тиску вздовж вертикального перерізу стінки (у вертикальній площині, проведеній нормально до стінки). Кожна ордината графіка, відміряна в напрямі, перпендикулярному до «стінки», являє собою гідростатичний тиск в даній точці «стінки». Площа графіка чисельно дає величину сили гідростатичного тиску, яка діє на одиницю ширини «стінки» (відміряну нормально до площини графіка). Позначаючи при побудові графіка ординати, що виражають гідростатичний тиск, не нормально до стінки, а по вертикальному й горизонтальному напрямках, отримують епюри складових сил гідроста-тичного тиску на стінку (відповідно вертикальної й горизонтальної складових).
Побудова епюр гідростатичного тиску базується на основному рівнянні гідростатики: [math]p=p_{0}+\rho gh[/math] а також на положенні, що гідростатичний тиск завжди нормальний до поверхні, на яку він діє.
Епюри гідростатичного тиску на вертикальну стінку
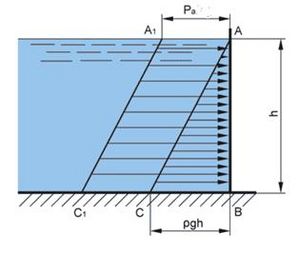
Допустимо вертикальна стінка АВ гідростатичної споруди (рис.1) затоплена рідиною з густиною ρ на висоту h Очевидно, що у точці А надлишковий гідростатичний тиск дорівнює нулю, так як [math]h = 0[/math], а повний тиск, дорівнює зовнішньому тиску pa у точці. Згідно з рівнянням гідростатики надлишковий тиск дорівнює [math]\rho gh[/math], а повний [math]p_{b}=p_{a}+\rho gh[/math]. Рівняння гідростатики, є рівнянням прямої лінії. Тому для побудови епюр надлишкового і повного тиску достатньо визначити тиск у двох точках і сполучити знайдені точки прямою лінією. Відкладемо по горизонтальній лінії від точки В значення ρgh, знайдену точку С сполучимо з точкою А. Отриманий відрізок АС і являє собою епюру надлишкового тиску на стінку АВ. Для отримання епюри повного тиску відкладемо по горизонталі від точок А і С відрізок, рівний pa, отримані точки А1 і С1 сполучимо прямою лінією А1С1, котра і буде епюрою повного тиску на вертикальну стінку. Для наглядності креслять (через довільний інтервал) стрілки, що показують величину і напрям дії тиску на стінку.Епюри гідростатичного тиску на плоску нахилену стінку
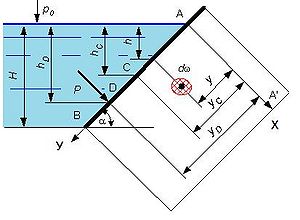
Допустимо (рис.2.1) стінка гідротехнічної споруди нахилена на кут a і затоплена на глибину h. Очевидно, що в точці А надлишковий гідростатичний тиск дорівнює нулю, а в точці B величині ρgh. Так як тиск на стінку діє по нормалі, то для побудови потрібно провести перпендикуляри до стінки у точках А і В. На перпендикулярі, що проходить через точку B відкладаємо відрізок, що дорівнює ρgh і сполучаємо отриману точку C прямою лінією з точкою А. Отримана пряма АС і є епюрою надлишкового тиску на стінку. Для побудови епюри повного тиску на перпендикулярах в точках А і В наносяться точки А1 і С1 на відстані, що дорівнює pа. Сполучивши точки А1 і С1, отримуємо епюру повного гідростатичного тиску. Так як і у першому випадку (див. рис.1) наноситься стрілки, що характеризують величину і напрям тиску.
[math]dP = pd \omega[/math] але [math]p = p_0+\rho gh[/math] тому [math]dP= p_{0}d \omega+\rho ghd \omega[/math] Виразимо останнє рівняння через координати положення площинки [math]d \omega[/math]. [math]dP = p_{0}d \omega + \rho gycos \alpha d \omega[/math] оскільки [math]h = ysin \alpha[/math] Проінтегруємо одержаний вираз, врахувавши заміну[math]y=\rho g[/math] [math]F=\int_{\omega}d\omega +ysin\alpha \int_{\omega}yd\omega[/math] де [math]\int_{\omega}d\omega =\omega[/math], a [math]int_{\omega}yd\omega[/math]- є статистичний момент [math]S_{x}[/math] ділянки, площею [math]\omega[/math] відносно осі x-ів (А-А’) Оскільки - [math]\int_{\omega}yd\omega =S_{x}=y_{c}\omega[/math] , то [math]P=p_{0}\omega + \rho gsin\alpha y_{c}\omega[/math] або [math]P=(p_{0} + \rho gh_{c})\omega[/math] (2.1) Таким чином, сила гідростатичного тиску на плоску похилу стінку рівна добутку площі стінки на гідростатичний тиск у центрі ваги стінки. З (2.1) випливає, що повна сила складається з сили зовнішнього тиску і сили надлишкового тиску. Рівнодійна сил зовнішнього тиску прикладена в центрі ваги поверхні стінки, оскільки зовнішній тиск однаковий у всіх точках простору, зайнятого рідиною. Результуюча сила ([math]P_{nadl.}=\rho gh_{c}\omega[/math]) надлишкового тиску не прикладена до центру поверхні стінки, оскільки надлишковий тиск змінний з глибиною. Координату точки прикладання рівнодійної сили надлишкового тиску можна знайти з рівняння моментів сил відносно осі x-ів. Тоді [math]F_{nadl.}\cdot y_{D}=\int_{\omega}\rho ghyd\omega[/math] Але [math]h=ysin\alpha[/math] , тому [math]F_{nadl.}\cdot y_{D}=\rho gsin\alpha \int_{\omega}y^{2}d\omega[/math](2.2) де[math]\int_{\omega}y^{2}d\omega[/math] - момент інерції [math]J_{x}[/math] поверхні, на яку тисне рідина відносно осі x-ів. З (2.2) отримуємо[math]y_{D}=\frac{\rho gsin\alpha J_{x}}{\rho gh_{c}\omega}=\frac{sin\alpha J_{x}}{y_{c}sin\alpha\omega}=\frac{J_{x}}{y_{c}\omega}[/math](2.3) Замінимо момент інерції відносно осі x-ів на момент відносно осі, що проходить через центр ваги поверхні : [math]J_{x}=y_{c}^{2}\omega+J_{c}[/math] Підставимо це значення у (2.3) [math]y_{D}=\frac{y_{c}^{2}\omega+J_{c}}{y_{c}\omega}=y_{c}\frac{J_{c}}{y_{c}\omega}[/math] (2.4) Таким чином, точка прикладання рівнодійної сили надлишкового тиску знаходиться у точці, розташованій нижче за центр ваги на відстані [math]\frac{J_{c}}{y_{c}\omega}[/math].