Відмінності між версіями «Критерії згоди»
GalkaPr (обговорення • внесок) |
GalkaPr (обговорення • внесок) |
||
| Рядок 40: | Рядок 40: | ||
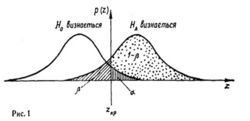
Співвідношення ймовірностей <math>\alpha </math> і <math>\beta </math> проілюстровано на рисунку 1, де наведено графіки розподілу ймовірностей при порівнянні арифметичних середніх, здобутих з двох вибірок: лівий зображає основну гіпотезу, правий альтернативну. | Співвідношення ймовірностей <math>\alpha </math> і <math>\beta </math> проілюстровано на рисунку 1, де наведено графіки розподілу ймовірностей при порівнянні арифметичних середніх, здобутих з двох вибірок: лівий зображає основну гіпотезу, правий альтернативну. | ||
| − | [[Файл: | + | [[Файл:Галочка.png|center|thumb|250px|Співвідношення ймовірностей прийняття гіпотез]] |
Версія за 23:34, 24 лютого 2012
| {{{img}}} | ||
| Імя | Галина | |
| Прізвище | Пригодська | |
| По-батькові | Миколаївна | |
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | СНм-11-241 | |
| Презентація доповіді на тему Критерії згоди є розміщеною в Репозиторії. |
До перевірки тієї чи іншої гіпотези доцільно підходити з різних теоретичних позицій. Кожна позиція ґрунтується на розподілі первинних або обчислених даних, які відрізняються від нормального розподілу. Це зумовлено обмеженим числом вимірювань або додатковими умовами при опрацюванні (обробці) дослідних даних. Характеристикою кожного розподілу є набір чисел, заздалегідь протабульованих. При перевірці гіпотези з дослідних даних складається число за тим же правилом, що й наведені в таблиці числа, і порівнюються з табличним числом. Гіпотеза визначається або відхиляється залежно від згоди дослідних і табличних чисел.
Критерій згоди - це табличне число, за допомогою якого приймається або відхиляється гіпотеза при проведенні досліду.
При порівнянні гіпотез є певне табличне значення і відповідна нерівність, яка задає співвідношення між цими значеннями.
Найвідоміші критерії згоди
Найвідоміші критерії згоди
- Хіквадрат Пірсона;
- Колмогорова;
- Стьюдента;
- Фішера.
Критерій Стьюдента
Нехай [math]x[/math] - нормально розподілена випадкова величина. При відомому СКВ [math]\sigma[/math] висувається основна гіпотеза [math]M\left( x \right)={{m}_{0}}[/math], або [math]M\left( x \right)-{{m}_{0}}=0[/math], тобто середнє значення або математичне сподівання [math]M\left( x \right)[/math] заданої сукупності, оцінюване на основі випадкової вибірки, не відрізняється від заданого значення [math]{{m}_{0}}[/math].
Альтернативна гіпотеза [math]{{H}_{A}}[/math], протилежна нуль-гіпотезі, тобто [math]M\left( x \right)\ne {{m}_{0}}[/math], або [math]M\left( x \right)-{{m}_{0}}\ne 0[/math]. Як критерії використовується відношення різниці порівнюваних величин [math]\widehat{x}-{{m}_{0}}[/math] до статистичної помилки [math]S/\sqrt{N}[/math] розрахункової величини [math]\widehat{x}[/math]:
[math]Z=\frac{\widehat{x}-{{m}_{0}}}{S}\sqrt{N}[/math]
, де [math]N[/math] – обсяг вибірки, [math]\widehat{x}[/math] - оцінка математичного сподівання генеральної сукупності.
[math]M{{\xi }_{t}}=\sum\limits_{i=1}^{N}{{{x}_{i}}{{p}_{i}}}[/math] - теоретичне математичне сподівання
[math]\widehat{m}=\frac{1}{N}\sum\limits_{i=1}^{N}{{{\xi }_{i}}}[/math] - оцінка математичного сподівання.
Статистична помилка, або помилка репрезентативності (відтворюваності) – це відхилення даного вибіркового показника від його справжнього значення в генеральній сукупності. Для вибіркового середнього це значення в [math]\sqrt{N}[/math] разів менше, ніж СКВ S.Згідно з теорією статистичної обробки обмеженого числа дослідних даних ймовірність значення Z розподілена за законом Стьюдента
[math]\rho \left( z \right)=\frac{1}{\sqrt{\pi \left( N-1 \right)}}\frac{r\left( \frac{N}{2} \right)}{r\left( \frac{N-1}{2} \right)}{{\left( 1+\frac{{{z}^{2}}}{N-1} \right)}^{-\frac{N}{2}}}[/math]
де r гамма-функція, табличні значення якої можна знайти в довідниках з математики або статистики.
Залежно від параметрів вибірки значення Z відрізняється від нуля, як міра відхилення вважається абсолютне значення [math]\left| z \right|[/math]. За прийнятим рівнем значущості [math]\alpha[/math] можна визначити таке критичне значення [math]{{z}_{}}[/math], що при вірній гіпотезі [math]{{H}_{0}}[/math] справедлива нерівність [math]\left| z \right|\ge {{z}_{kp}}[/math], тобто [math]\rho \left( \left| z \right|\ge {{z}_{kp}} \right)=\alpha[/math].
Якщо число z , обчислене за вибіркою, задовольняє нерівність [math]\left| z \right|\lt {{z}_{kp}}[/math], то вважатимемо що відхилення z від 0 можна розглядати як випадкове. Тоді говорять, що нуль гіпотеза не відхиляється на основі вибірки, або немає підстав для її відхилення.
Якщо [math]\left| z \right|\ge {{z}_{kp}}[/math], , то при справедливій нуль гіпотезі таке відхилення можливе, але малоймовірне. Тоді вважають більш ймовірним, що нуль гіпотеза невірна, і її відхиляють. При аналізі рішень слід мати на увазі обидва можливі типи помилок.
Співвідношення ймовірностей [math]\alpha[/math] і [math]\beta[/math] проілюстровано на рисунку 1, де наведено графіки розподілу ймовірностей при порівнянні арифметичних середніх, здобутих з двох вибірок: лівий зображає основну гіпотезу, правий альтернативну.