Відмінності між версіями «Повний факторний експеримент (ПФЕ)»
Pob (обговорення • внесок) |
Pob (обговорення • внесок) |
||
| Рядок 68: | Рядок 68: | ||
Таблиця розрахунків: | Таблиця розрахунків: | ||
| − | <center>[[Файл:pic4.jpg]] </center> | + | <center>[[Файл:pic4.jpg]] </center><br /> |
| + | <center>[[Файл:pic5.jpg]] </center> | ||
| + | |||
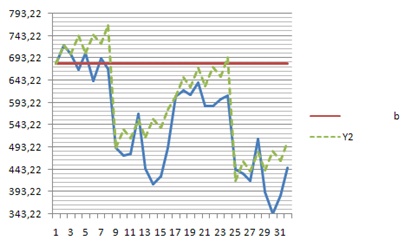
<center>Рисунок 4 – Порівняння дійсного значення результату експерименту та зпрогнозованого результату</center> | <center>Рисунок 4 – Порівняння дійсного значення результату експерименту та зпрогнозованого результату</center> | ||
Версія за 13:56, 19 березня 2010
Зміст
Повний факторний експеримент (ПФЕ)
- Таблиця значень або рівнів факторів повинна мати лінійно не залежні стовбці,сума добутків значень будь яких двох факторів (чисел 2вох стовбців)
повинна бути рівна нулю. Тобто повний факторний експеримент має ортогональну матрицю.
ПФЕ- експеримент що реалізує всі можливі неповторювані комбінації рівнів незалежних змінних, кожна з яких примусово(активно) варіює на двох рівнях.
Число цих комбінацій при N факторах рівна двом в степені N і визначає тип планування.
Опис експерименту:
(задача взята з даного джерела: [1])
- Мета: визначити вплив факторів механічної обробки на керамічну міцність.
Кількість серій = значення (більше 15 серій) керамічної міцності.
Кількість спостережень =32 (25 завершених факторних проектів).
Величина відклику Y = Значення (більше 15 представлень) керамічної міцності.
- Фактор 1 = Таблична швидкість (2 рівня:повільний(.025 м\с) і швидкий(.125 м\с) )
- Фактор 2 = Нижня Норма подачі (2 рівня:повільний(.05м\с) і швидкий (ю125м\с))
- Фактор 3 = Колесо Гріт (2 рівня: 140/170 и 80/100)
- Фактор 4 = Напрямок (2 рівня: повздовжний і поперечний)
- Фактор 5 = Партія (2 рівня: 1 и 2)
Так як 2 ва фактора якісні (напрямок і партія), і відповідно розумно очікувати монотонниі ефекти від кількісних факторів, без включення виконань
центральних точок.
Побудова матриці ПФЕ.
- В основі повного факторнго експеременту лежить матриця планування яка включає все можливий перебір неповторюваних комбінацій рівнів.
- Побудову матриці зручно починати з рядка де всі керовані змінні перебувають на нижньому рівні, тобто :
Далі зручно скористатися правилом, що частота зміни знака для кожних
керованих змінних у двічі менша ніж попередня.
Відповідно отримуємо матрицю ПФЕ з пятьма факторами:
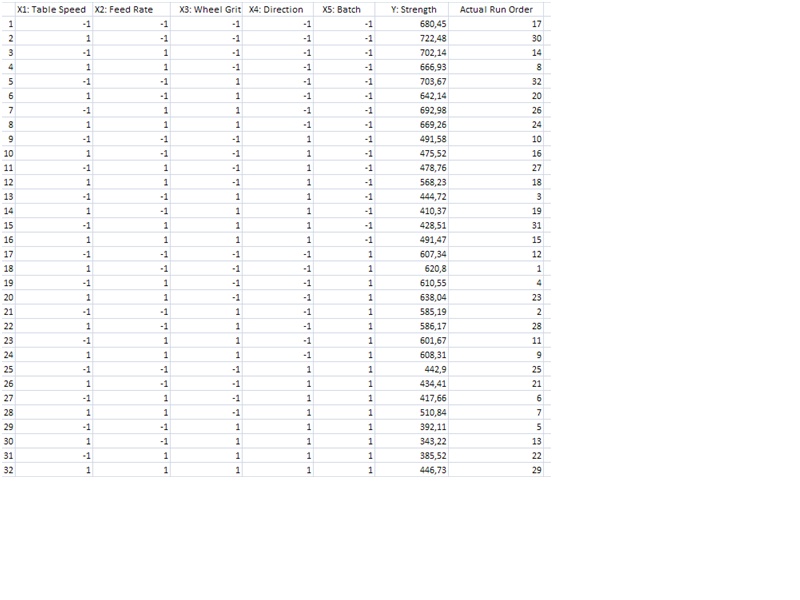
Властивості матриці ПФЕ
- Відповідно для якої кількість рядків якої буде рівна кількості експериментів 2N (де в нашому випадку кількість факторів N = 5).
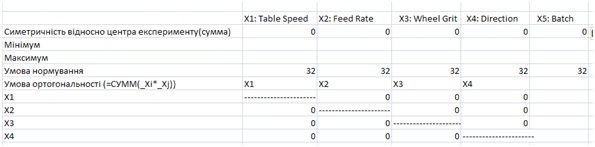
Побудований таким чином план експериментів має відповідно такі властивості:
- - Симетричності відносно центра експерименту (тобто сума елементів стовбців рівна нулю);
- - Нормування (тобто сума елементів стовбців по модулю рівна кількості експериментів);
- - Ортогональності (Сума добутку i – того елементу одного ствобця на відповідний і – тий елемент будь-якого іншого рівна нулю);
- Оскільки зміна вихідної величини y має випадковий характер то доводиться проводити m дослідів при кожному наборі факторів і
відповідно результати усереднювати.Тобто весь експеримент ділиться на m серій дослідів в якому повністю реалізується матриця
планування.Перед реалізацією плану на обєкті варто рендомізувати серію дослідів (тобто надати випадковий номер рядку матриці
планування). Рандомізація необхідна для виключення деяких системних помилок, тобто впливу побічних факторів на величину відклику
при верхньому або нижньому рівні фіксованого фактора.
- В нашому випадку проведено m>15 серій дослідів з метою отримання як найменшого середнього значення квадрату відхилення від
математичного сподівання результуючої величини. І відповідно в таблиці в нас показано (керамічна міцність) відношення суми
значень отриманих при і-тому наборі факторів в m серіях дослідів відповідно до m (кількості серій дослідів).
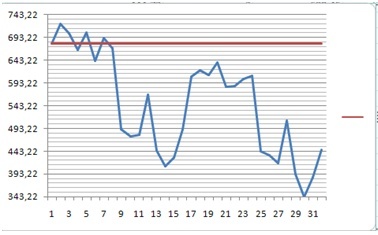
- На рисунку 3 відображено графік зміни показника вихідної величини в порівнянні з експериментом
у якому всі фактори перебувають на нижньому рівні і відповідно мають мінімальний вплив на вихідну
величину. На основі цих данних я інтуєтивно прослідкував певну залежність керамічної міцності від
того які з факторів перебувають на вищому рівні тобто виділивши множину комбінацій рівнів де в нас
лише один фактор перебуває на вищому рівні а всі інші на нижчому обраховую певний коефіцієнт впливу
відповідно на результат експерименту (Y) як різницю Аj=(Yxi=0 – Y) де i=1..5, j=1..5, Аj – визначений
мною коефіцієнт впливу j – того фактора, Yxi=0 – результат експерименту при перебуванні усіх факторів на
нижньому рівні. Відповідно побудував нову прогнозовану мною множину результатів експеременту на основі
вище згаданого алгоритму (рисунок 4.)
Таблиця розрахунків:
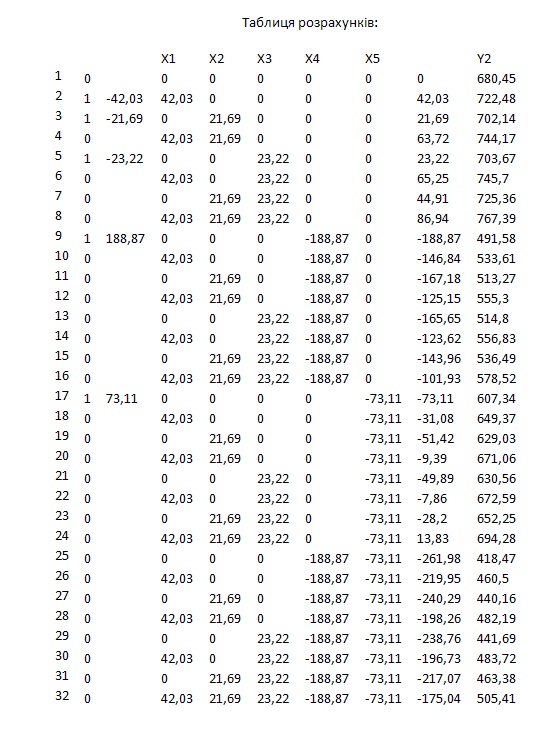
Висновки
- Для оцінки якості визначеного мною коефіцієнта впливу факторів проводжу розрахунок середнього відхилення зпрогнозованого значення від дійсного яке склало 46,034063 , середній процент відхилення від дійсного значення результату експерименту становить 8,7930604%, що на мою думку враховуючи стохастичну природу процесу є досить не поганим результатом і тому відповідно за даною, розробленою мною, методикою можна визначити кількісні значення коефіцієнтів впливу факторів на результуючу величину і на основі цих значень прийняти рішення, щодо важливості врахування тих чи інших факторів.