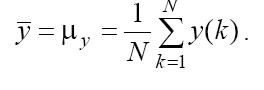Відмінності між версіями «Кореляційний аналіз»
Inna (обговорення • внесок) (→Список використаних джерел) |
|||
| (Не показані 26 проміжних версій 8 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
| − | {{ | + | {{Невідредаговано}} |
| − | + | {{Студент | Name= Інна| Surname= Канєвська| FatherNAme=|Faculti=ФІС | Group=СНм-51 | Zalbook=}} | |
....... Презентація доповіді (університетський репозиторій). | ....... Презентація доповіді (університетський репозиторій). | ||
| Рядок 7: | Рядок 7: | ||
'''Кореляційний аналіз''' – це статистичне дослідження (стохастичної) залежності між випадковими величинами (англ. correlation – взаємозв’язок). У найпростішому випадку досліджують дві вибірки (набори даних), у загальному – багатовимірні комплекси (групи) геологічних параметрів або об’єктів. | '''Кореляційний аналіз''' – це статистичне дослідження (стохастичної) залежності між випадковими величинами (англ. correlation – взаємозв’язок). У найпростішому випадку досліджують дві вибірки (набори даних), у загальному – багатовимірні комплекси (групи) геологічних параметрів або об’єктів. | ||
| − | '''Мета кореляційного аналізу''' – забезпечити отримання деякої інформації про одну змінну за допомогою іншої змінної. В випадках, коли можливе досягнення мети, говорять, що змінні корелюють. В | + | '''Мета кореляційного аналізу''' – забезпечити отримання деякої інформації про одну змінну за допомогою іншої змінної. В випадках, коли можливе досягнення мети, говорять, що змінні корелюють. В загальному вигляді сприйняття гіпотези про наявність кореляції означає, що зміна значення змінної А відбудеться одночасно з пропорційною зміною значення В. |
Мірою залежності між експериментальними наборами даних є числа – коефіцієнти зв’язку. | Мірою залежності між експериментальними наборами даних є числа – коефіцієнти зв’язку. | ||
| Рядок 66: | Рядок 66: | ||
Напівчасткова кореляція названа так, тому що дисперсія контрольованої змінної (Х2) усувається з іншої незалежної змінної (Х1), але не із залежної змінної (Y). Тобто ми позбавляємось лише впливу Х2 на Х1. | Напівчасткова кореляція названа так, тому що дисперсія контрольованої змінної (Х2) усувається з іншої незалежної змінної (Х1), але не із залежної змінної (Y). Тобто ми позбавляємось лише впливу Х2 на Х1. | ||
| − | + | <center> | |
| + | [[Файл:1_3.jpg]] | ||
Рис. 1.3 - Ілюстрація напівчасткової кореляції | Рис. 1.3 - Ілюстрація напівчасткової кореляції | ||
| + | </center> | ||
У випадку трьох змінних формула для обчислення напівчасткової кореляції буде мати вигляд: | У випадку трьох змінних формула для обчислення напівчасткової кореляції буде мати вигляд: | ||
| − | + | ||
| + | <math>r_{_{Y(1.2)}}^{2}=R_{Y.12}^{2}-r_{Y2}^{2}</math> | ||
| + | |||
В термінах звичайних коефіцієнтів кореляції отримаємо: | В термінах звичайних коефіцієнтів кореляції отримаємо: | ||
| − | |||
| − | |||
| − | - результат кореляції між у і х2 та х1 і х2 | + | <math>r_{Y(1.2)}^{2}=\frac{{{({{r}_{Y1}}-{{r}_{Y2}}{{r}_{12}})}^{2}}}{1-r_{12}^{2}}</math> |
| + | |||
| + | |||
| + | <math>{{r}_{Y(1.2)}}=\frac{{{r}_{Y1}}-{{r}_{Y2}}{{r}_{12}}}{\sqrt{1-r_{12}^{2}}}</math> | ||
| + | |||
| + | де <math>{{r}_{Y1}}</math> - проста кореляція між | ||
| + | |||
| + | |||
| + | <math>{{r}_{Y2}}{{r}_{12}}</math> - результат кореляції між у і х2 та х1 і х2 | ||
| − | |||
| + | <math>\sqrt{1-r_{_{12}}^{2}}</math> - загальна дисперсія за винятком взаємозв’язку між <math>{{x}_{1}}</math> та <math>{{x}_{2}}</math>. | ||
| + | |||
Часткова кореляція відрізняється від напівчасткової тим, що усувається вплив третьої змінної з іншої незалежної змінної, а також і з залежної змінної. | Часткова кореляція відрізняється від напівчасткової тим, що усувається вплив третьої змінної з іншої незалежної змінної, а також і з залежної змінної. | ||
| + | <center> | ||
| + | [[Файл:1_4.jpg]] | ||
Рис. 1.4 - Ілюстрація часткової кореляції | Рис. 1.4 - Ілюстрація часткової кореляції | ||
| − | + | </center> | |
У випадку трьох змінних формула для обчислення часткової кореляції буде мати вигляд: | У випадку трьох змінних формула для обчислення часткової кореляції буде мати вигляд: | ||
| + | <math>r_{Y1.2}^{2}=\frac{R_{Y.12}^{2}-r_{Y2}^{2}}{1-r_{Y2}^{2}}</math> | ||
В термінах звичайних коефіцієнтів кореляції отримаємо: | В термінах звичайних коефіцієнтів кореляції отримаємо: | ||
| − | + | <math>r_{Y1.2}^{2}=\frac{({{r}_{Y1}}-{{r}_{Y2}}{{r}_{12}})}{(1-r_{Y2}^{2})(1-r_{Y2}^{2})}</math> | |
| − | + | ||
| + | <math>{{r}_{Y1.2}}=\frac{{{r}_{Y1}}-{{r}_{Y2}}{{r}_{12}}}{\sqrt{(1-r_{Y2}^{2})(1-r_{Y2}^{2})}}</math> | ||
| + | |||
| + | де <math>{{r}_{Y1}}</math> - <math>y</math> та <math>{{x}_{1}}</math> | ||
| + | |||
| + | <math>{{r}_{Y2}}{{r}_{12}}</math> - результат кореляції між у і х2 та х1 і х2 | ||
| + | |||
| + | <math>\sqrt{1-r_{_{12}}^{2}}</math> - загальна дисперсія за винятком всіх часткових взаємозв’язків між <math>{{x}_{1}}</math> і <math>{{x}_{2}}</math> | ||
| + | |||
| + | Якщо кореляція між х1 і х2 та у і х2 відсутня, то <math>{{r}_{Y1.2}}={{r}_{Y1}}</math> | ||
| + | |||
| + | =Властивості коефіцієнта кореляції= | ||
| + | |||
| + | 1. Коефіцієнт кореляції є в межах від -1 до +1. | ||
| + | |||
| + | <math>-1\le \rho (x,y)\le +1</math> | ||
| + | |||
| + | Якщо <math>\rho (x,y)>0</math>, то кореляція пряма, а якщо <math>\rho (x,y)<0</math> – зворотна. Пряма кореляція: більшим значенням випадкової змінної <math>x</math> відповідають більші значення <math>y</math>; зворотна кореляція: більшим значенням <math>x</math> відповідають менші <math>y</math> і навпаки, більшим <math>y</math> – менші <math>x</math>. | ||
| + | |||
| + | 2. Симетрія | ||
| + | |||
| + | <math>\rho (x,y)=\rho (y,x)</math> | ||
| + | |||
| + | 3. Якщо <math>x</math> та <math>y</math> пов’язані лінійним функціональним зв’язком <math>y\left( x \right)=a+bx</math>, <math>a</math> i <math>b</math> – сталі, то <math>\left| \rho (x,y) \right|=1</math>, і навпаки. | ||
| + | |||
| + | 4. Якщо випадкові змінні лінійно незалежні, то <math>\rho (x,y)=0</math>, і навпаки. | ||
| + | Останні дві властивості можна сформулювати як необхідну й достатню умови, причому критерієм залежності випадкових величин <math>x</math> і <math>y</math> є відмінність коефіцієнта кореляції від нуля: <math>r\ne 0</math>. | ||
| + | |||
| + | =Кореляційне поле = | ||
| + | Графічно дані для кореляційного аналізу зображають у вигляді кореляційного поля, тобто точок на площині, кожна з яких має координати <math>({{x}_{i}},{{y}_{i}})</math> (рис.3.1) | ||
| + | |||
| + | <center> | ||
| + | [[Файл:6.jpg]] | ||
| + | |||
| + | Рис. 3.1. Візуальна оцінка характеру кореляційного зв’язку <br> | ||
| + | за кореляційним полем: ''a'' – пряма кореляція, <math>r>0</math>; ''б'' – зворотна кореляція, <math>r<0</math>. | ||
| + | </center> | ||
| + | <br> | ||
| + | Для прямої кореляції характерною тенденцією є збільшення одного з параметрів, якщо збільшується інший, а для оберненої, навпаки: збільшення одного супроводжується, як звичайно, зменшенням іншого. Причиною фіктивної кореляції (тобто такої, що спостережена, але не властива природним об’єктам) може бути неоднорідність сукупності даних, які відображають два різні об’єкти (рис. 3.2). Іноді методика дослідження впливає на створення видимості зв’язку там, де його немає. Наприклад, якщо вимірювати довжину і ширину без урахування орієнтації зразків, то всі точки кореляційного поля лежатимуть у секторі від 0 до 45° (замість сектора 0–90°), що помилково можна сприйняти як наявність деякого зв’язку | ||
| + | |||
| + | <center> | ||
| + | [[Файл:7.jpg]] | ||
| + | |||
| + | Рис. 3.2. Некорельовані дані, <math>r=0</math> і фіктивна кореляція (неоднорідні дані). | ||
| + | </center> | ||
| + | |||
| + | =Перевірка гіпотези про значущість коефіцієнта кореляції= | ||
| + | |||
| + | Згідно зі схемою статистичного доведення виконуємо таке. | ||
| + | 1. Нульова гіпотеза: лінійного зв’язку немає, тоді істинний коефіцієнт кореляції дорівнює нулю: | ||
| + | |||
| + | <math>{{H}_{0}}:\rho (x,y)=0</math> | ||
| + | |||
| + | за двосторонньої альтернативи | ||
| + | |||
| + | <math>{{H}_{1}}:\rho (x,y)\ne 0</math> | ||
| + | |||
| + | 2. Вибираємо <math>\alpha </math>, наприклад, <math>\alpha =0,05</math>. | ||
| + | |||
| + | 3. Обчислюємо вибірковий коефіцієнт кореляції <math>r</math> і будуємо статистику | ||
| + | |||
| + | <math>t=\frac{r}{\sqrt{1-{{r}^{2}}}}\sqrt{n-2}</math> | ||
| + | |||
| + | 4. Ця статистика має розподіл Стьюдента з <math>df=n-2</math> ступенями вільності, а для <math>n>60</math> можна використовувати й стандартний закон розподілу. | ||
| + | |||
| + | 5. Знаходимо критичні значення статистики, тобто квантилі розподілу Стьюдента (чи стандартного для великих вибірок) для заданого рівня значущості <math>\alpha </math>. Для <math>n\le 60</math> маємо | ||
| + | <math>{{t}_{Kp}}={{t}_{Kp}}(\alpha ,d,f)</math>, а для <math>n>60</math> – наближену формулу | ||
| + | <math>{{t}_{Kp}}=\psi (\alpha )</math>, | ||
| + | де <math>\psi (\alpha )={{\Phi }^{-1}}(\alpha )</math> - обернена функція стандартного закону розподілу. | ||
| + | |||
| + | 6. Перевіряємо критерій: якщо <math>\left| t \right|\ge {{t}_{Kp}}</math>, то нульову гіпотезу відхиляємо, тобто існує суттєвий лінійний зв’язок між даними (дані корелюють). | ||
| + | На практиці зручнішою є формула, яка дає критичне значення самого коефіцієнта кореляції. З рівняння статистики можна визначити | ||
| + | <math>{{r}_{Kp}}=\frac{{{t}_{Kp}}}{\sqrt{n-2+t_{Kp}^{2}}}</math> | ||
| + | Ця формула дає змогу один раз відшукати критичне значення коефіцієнта кореляції (для фіксованого <math>\alpha </math> і <math>n</math>) і використовувати його в наступній серії порівнянь парних коефіцієнтів кореляції з критичним, наприклад, для перевірки на значущість коефіцієнтів кореляційної матриці. | ||
| + | |||
| + | =Автокореляція= | ||
| + | Автокореляція або автокореляційна функція - це кореляція функції з самою собою зміщеною на певну величину незалежної змінної. Автокореляція використовується для знаходження закономірностей в ряді даних, таких як періодичність. Часто застосовується у статистиці та обробці сигналів для аналізу функцій або серій даних. | ||
| + | Математично автокореляційна функція визначається як: | ||
| + | |||
| + | <math>{{R}_{f}}(\tau )=\int\limits_{-\infty }^{\infty }{f(t){{f}^{*}}(t-\tau )}dt</math>, | ||
| + | |||
| + | де функція <math>f(t)</math> інтегрується у добутку з комплексно спряженою та зміщеною на певну величину <math>\tau </math> (часто <math>\tau </math> це час) функцією. | ||
| + | |||
| + | =Кореляційна матриця= | ||
| + | Нехай маємо групу з <math>k</math> випадкових змінних <math>{{x}_{1}},...,{{x}_{k}}</math> (досліджуваних параметрів), що представлені вибірками обсягу <math>n</math> кожна. Для усіх можливих різних пар індексів <math>i,j=1,2,...,k</math> можна обчислити парні коефіцієнти кореляції <math>{{r}_{ij}}=r({{x}_{i}},{{x}_{j}})</math>. | ||
| + | Для <math>i=j</math>, тобто для двох ідентичних наборів, можна прийняти <math>{{r}_{i}}_{j}=1</math>, що відповідає лінійній функціональній залежності <math>{{x}_{i}}={{x}_{j}}</math> (тотожності) для всіх пар значень у вибірках. Коефіцієнти кореляції запишемо у вигляді підсумкової симетричної матриці | ||
| + | |||
| + | <math>R=\left[ \begin{matrix} | ||
| + | 1 & {{r}_{12}} & ... \\ | ||
| + | {{r}_{21}} & 1 & ... \\ | ||
| + | ... & ... & ... \\ | ||
| + | {{r}_{k1}} & {{r}_{k2}} & ... \\ | ||
| + | \end{matrix} \right..</math> | ||
| + | |||
| + | Після перевірки кожного з коефіцієнтів на значущість (достатньо це зробити для елементів матриці над головною діагоналлю) і заміни коефіцієнтів, що менше <math>{{r}_{Kp}}</math>, нулем, “очищена” кореляційна матриця відображає “справжні” статистично значимі зв’язки між змінними. | ||
| + | Аналіз структури кореляційної матриці є дуже важливим методом для виявлення, наприклад, парагенетичних асоціацій у геохімічних дослідженнях , а також основою інших методів аналізу (наприклад, факторного). З огляду на це часто виникає завдання порівняти різні коефіцієнти кореляції. Оскільки істинні коефіцієнти кореляції <math>{{\rho }_{i}}</math>, та <math>{{\rho }_{j}}</math> невідомі, то рішення ухвалюють, користуючись їхніми вибірковими оцінками <math>{{r}_{i}}</math> та <math>{{r}_{j}}</math>на підставі статистичного доведення. | ||
| + | |||
| + | 1. Формулюємо нульову гіпотезу про рівність коефіцієнтів кореляції | ||
| + | |||
| + | <math>{{H}_{0}}:{{\rho }_{i}}={{\rho }_{j}}</math> | ||
| + | |||
| + | та альтернативну їй | ||
| + | |||
| + | <math>{{H}_{1}}:{{\rho }_{i}}\ne {{\rho }_{j}}</math> | ||
| + | |||
| + | 2. Вибираємо рівень значущості <math>\alpha </math>. | ||
| + | |||
| + | 3. Оскільки розподіл коефіцієнтів кореляції за умови <math>\rho \ne 0</math> має значну асиметрію, то використовуємо перетворені величини | ||
| + | |||
| + | <math>z{}_{i}=\frac{1}{2}\ln \frac{1+{{r}_{i}}}{1-{{r}_{i}}}</math> | ||
| + | |||
| + | і будуємо статистику | ||
| + | |||
| + | |||
| + | <math>{{t}^{*}}=\frac{\left| {{z}_{i}}-{{z}_{j}} \right|}{s\sqrt{2}}</math> <math>s=1/\sqrt{n-3}</math> | ||
| + | |||
| + | 4. В умовах гіпотези <math>{{H}_{0}}</math> статистика <math>{{t}^{*}}</math> має асимптотично нормальний розподіл з нульовим середнім та дисперсією, що дорівнює 1. | ||
| + | |||
| + | 5. Знаходимо критичні значення статистики, тобто квантилі стандартного нормального розподілу, наприклад, для <math>\alpha =0,05</math> маємо <math>{{t}^{*}}={{\psi }^{-1}}(0,05)=1,96</math>. | ||
| − | + | 6. Якщо | |
| − | - | + | <math>\left| {{z}_{i}}-{{z}_{j}} \right|<{{t}^{*}}s\sqrt{2}</math> |
| − | + | то гіпотеза про рівність коефіцієнтів не суперечить вибірковим даним (для заданого <math>\alpha </math>). | |
=Список використаних джерел= | =Список використаних джерел= | ||
| Рядок 113: | Рядок 245: | ||
{{Завдання:Виступ|inna|9 березня 2010|Кореляційний аналіз експериментальних даних. Кореляційна матриця. Перевірка гіпотез відносно значень кореляційної матриці}} | {{Завдання:Виступ|inna|9 березня 2010|Кореляційний аналіз експериментальних даних. Кореляційна матриця. Перевірка гіпотез відносно значень кореляційної матриці}} | ||
| − | |||
[[Категорія:Виступ на семінарі]] | [[Категорія:Виступ на семінарі]] | ||
| − | [[Категорія:Планування | + | [[Категорія:Планування експерименту]] |
| − | |||
| − | |||
Поточна версія на 10:06, 20 березня 2012
| Цю статтю потрібно відредагувати. Щоб вона відповідала ВИМОГАМ. |
| {{{img}}} | ||
| Імя | Інна | |
| Прізвище | Канєвська | |
| По-батькові | ||
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | ||
....... Презентація доповіді (університетський репозиторій).
Зміст
Кореляційний аналіз, мета і завдання
Кореляційний аналіз – це статистичне дослідження (стохастичної) залежності між випадковими величинами (англ. correlation – взаємозв’язок). У найпростішому випадку досліджують дві вибірки (набори даних), у загальному – багатовимірні комплекси (групи) геологічних параметрів або об’єктів.
Мета кореляційного аналізу – забезпечити отримання деякої інформації про одну змінну за допомогою іншої змінної. В випадках, коли можливе досягнення мети, говорять, що змінні корелюють. В загальному вигляді сприйняття гіпотези про наявність кореляції означає, що зміна значення змінної А відбудеться одночасно з пропорційною зміною значення В.
Мірою залежності між експериментальними наборами даних є числа – коефіцієнти зв’язку.
Головні завдання кореляційного аналізу:
1) оцінка за вибірковими даними коефіцієнтів кореляції;
2) перевірка значущості вибіркових коефіцієнтів кореляції або кореляційного відношення;
3) оцінка близькості виявленого зв’язку до лінійного;
4) побудова довірчого інтервалу для коефіцієнтів кореляції.
Визначення сили та напрямку взаємозв’язку між змінними є однією з важливих проблем аналізу даних. В загальному випадку для цього застосовують поняття кореляції.
Поняття кореляції
Коефіцієнт кореляції, а в загальному випадку кореляційна функція, дозволяють встановити степінь взаємозв’язку між змінними. Кореляція може бути лінійною або нелінійною в залежності від типу залежності, яка фактично існує між змінними. Досить часто на практиці розглядають тільки лінійну кореляцію (взаємозв’язок), але більш глибокий аналіз потребує використання для дослідження процесів нелінійних залежностей. Складну нелінійну залежність можна спростити, але знати про її існування необхідно для того, щоб побудувати адекватну модель процесу.
Рис. 1.1 - Ілюстрація «простої» кореляції
Формула для обчислення коефіцієнтів кореляції має вигляд:
де N − довжина вибірки даних; x, y − середні вибіркові x, y ; σx,σ y − стандартні відхилення, тобто корені квадратні з їх дисперсій.
Наприклад,
де N − число вимірів змінної y ; y − середнє значення ряду {y(k)}, яке обчислюється за формулою:
Часткова та напівчасткова кореляції
У випадку двох нормальних або майже нормальних величин коефіцієнт кореляції між ними може бути використаний як міра взаємозв’язку і це підтверджено багатьма практичними результатами. Проте при інтерпретації «взаємозв’язку» часто виникають наступні труднощі: якщо одна величина корельована с іншою, то це може бути відображенням того факту, що вони обидві корельовані з деякою третьою величиною або з сукупністю величин, які залишаються за кадром і не введені в модель. Така ситуація приводить до розгляду умовних кореляцій між двома величинами при фіксованих значеннях інших величин. Це так звані часткові кореляції. Якщо кореляція між двома величинами зменшується, коли ми фіксуємо деяку іншу випадкову величину, то це означає, що їх взаємозв’язок виникає частково через вплив цієї величини. Якщо ж часткова кореляція дорівнює нулю або дуже мала, то робимо висновок, що їх взаємозв’язок цілком обумовлений власним впливом і ніяк не пов’язаний з третьою величиною.
І навпаки, якщо часткова кореляція більше початкової кореляції між двома величинами, то ми робимо висновок, що інші величини ослабили зв’язок, або приховали (замазали) кореляцію.
Розрізняють поняття напівчасткової та часткової кореляції. Розглянемо ситуацію для трьох змінних (два при Х1 та Х2 (пояснюючі, незалежні змінні) і одна змінна відклику Y (залежна змінна, змінна критерію)). Часткова та напівчасткова кореляції позбавляють впливу третьої змінної.
Рис. 1.2 - Ілюстрація кореляції трьох змінних
Значення напівчасткової та часткової кореляції можна виразити через множинну кореляцію. Множинна кореляція у випадку трьох змінних обчислюється за формулою:
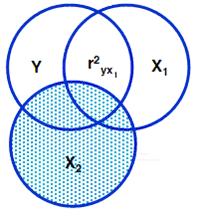
Напівчасткова кореляція названа так, тому що дисперсія контрольованої змінної (Х2) усувається з іншої незалежної змінної (Х1), але не із залежної змінної (Y). Тобто ми позбавляємось лише впливу Х2 на Х1.
Рис. 1.3 - Ілюстрація напівчасткової кореляції
У випадку трьох змінних формула для обчислення напівчасткової кореляції буде мати вигляд:
[math]r_{_{Y(1.2)}}^{2}=R_{Y.12}^{2}-r_{Y2}^{2}[/math]
В термінах звичайних коефіцієнтів кореляції отримаємо:
[math]r_{Y(1.2)}^{2}=\frac{{{({{r}_{Y1}}-{{r}_{Y2}}{{r}_{12}})}^{2}}}{1-r_{12}^{2}}[/math]
[math]{{r}_{Y(1.2)}}=\frac{{{r}_{Y1}}-{{r}_{Y2}}{{r}_{12}}}{\sqrt{1-r_{12}^{2}}}[/math]
де [math]{{r}_{Y1}}[/math] - проста кореляція між
[math]{{r}_{Y2}}{{r}_{12}}[/math] - результат кореляції між у і х2 та х1 і х2
[math]\sqrt{1-r_{_{12}}^{2}}[/math] - загальна дисперсія за винятком взаємозв’язку між [math]{{x}_{1}}[/math] та [math]{{x}_{2}}[/math].
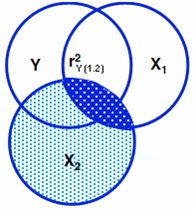
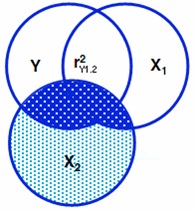
Часткова кореляція відрізняється від напівчасткової тим, що усувається вплив третьої змінної з іншої незалежної змінної, а також і з залежної змінної.
Рис. 1.4 - Ілюстрація часткової кореляції
У випадку трьох змінних формула для обчислення часткової кореляції буде мати вигляд:
[math]r_{Y1.2}^{2}=\frac{R_{Y.12}^{2}-r_{Y2}^{2}}{1-r_{Y2}^{2}}[/math]
В термінах звичайних коефіцієнтів кореляції отримаємо:
[math]r_{Y1.2}^{2}=\frac{({{r}_{Y1}}-{{r}_{Y2}}{{r}_{12}})}{(1-r_{Y2}^{2})(1-r_{Y2}^{2})}[/math]
[math]{{r}_{Y1.2}}=\frac{{{r}_{Y1}}-{{r}_{Y2}}{{r}_{12}}}{\sqrt{(1-r_{Y2}^{2})(1-r_{Y2}^{2})}}[/math]
де [math]{{r}_{Y1}}[/math] - [math]y[/math] та [math]{{x}_{1}}[/math]
[math]{{r}_{Y2}}{{r}_{12}}[/math] - результат кореляції між у і х2 та х1 і х2
[math]\sqrt{1-r_{_{12}}^{2}}[/math] - загальна дисперсія за винятком всіх часткових взаємозв’язків між [math]{{x}_{1}}[/math] і [math]{{x}_{2}}[/math]
Якщо кореляція між х1 і х2 та у і х2 відсутня, то [math]{{r}_{Y1.2}}={{r}_{Y1}}[/math]
Властивості коефіцієнта кореляції
1. Коефіцієнт кореляції є в межах від -1 до +1.
[math]-1\le \rho (x,y)\le +1[/math]
Якщо [math]\rho (x,y)\gt 0[/math], то кореляція пряма, а якщо [math]\rho (x,y)\lt 0[/math] – зворотна. Пряма кореляція: більшим значенням випадкової змінної [math]x[/math] відповідають більші значення [math]y[/math]; зворотна кореляція: більшим значенням [math]x[/math] відповідають менші [math]y[/math] і навпаки, більшим [math]y[/math] – менші [math]x[/math].
2. Симетрія
[math]\rho (x,y)=\rho (y,x)[/math]
3. Якщо [math]x[/math] та [math]y[/math] пов’язані лінійним функціональним зв’язком [math]y\left( x \right)=a+bx[/math], [math]a[/math] i [math]b[/math] – сталі, то [math]\left| \rho (x,y) \right|=1[/math], і навпаки.
4. Якщо випадкові змінні лінійно незалежні, то [math]\rho (x,y)=0[/math], і навпаки. Останні дві властивості можна сформулювати як необхідну й достатню умови, причому критерієм залежності випадкових величин [math]x[/math] і [math]y[/math] є відмінність коефіцієнта кореляції від нуля: [math]r\ne 0[/math].
Кореляційне поле
Графічно дані для кореляційного аналізу зображають у вигляді кореляційного поля, тобто точок на площині, кожна з яких має координати [math]({{x}_{i}},{{y}_{i}})[/math] (рис.3.1)
Рис. 3.1. Візуальна оцінка характеру кореляційного зв’язку
за кореляційним полем: a – пряма кореляція, [math]r\gt 0[/math]; б – зворотна кореляція, [math]r\lt 0[/math].
Для прямої кореляції характерною тенденцією є збільшення одного з параметрів, якщо збільшується інший, а для оберненої, навпаки: збільшення одного супроводжується, як звичайно, зменшенням іншого. Причиною фіктивної кореляції (тобто такої, що спостережена, але не властива природним об’єктам) може бути неоднорідність сукупності даних, які відображають два різні об’єкти (рис. 3.2). Іноді методика дослідження впливає на створення видимості зв’язку там, де його немає. Наприклад, якщо вимірювати довжину і ширину без урахування орієнтації зразків, то всі точки кореляційного поля лежатимуть у секторі від 0 до 45° (замість сектора 0–90°), що помилково можна сприйняти як наявність деякого зв’язку
Рис. 3.2. Некорельовані дані, [math]r=0[/math] і фіктивна кореляція (неоднорідні дані).
Перевірка гіпотези про значущість коефіцієнта кореляції
Згідно зі схемою статистичного доведення виконуємо таке. 1. Нульова гіпотеза: лінійного зв’язку немає, тоді істинний коефіцієнт кореляції дорівнює нулю:
[math]{{H}_{0}}:\rho (x,y)=0[/math]
за двосторонньої альтернативи
[math]{{H}_{1}}:\rho (x,y)\ne 0[/math]
2. Вибираємо [math]\alpha[/math], наприклад, [math]\alpha =0,05[/math].
3. Обчислюємо вибірковий коефіцієнт кореляції [math]r[/math] і будуємо статистику
[math]t=\frac{r}{\sqrt{1-{{r}^{2}}}}\sqrt{n-2}[/math]
4. Ця статистика має розподіл Стьюдента з [math]df=n-2[/math] ступенями вільності, а для [math]n\gt 60[/math] можна використовувати й стандартний закон розподілу.
5. Знаходимо критичні значення статистики, тобто квантилі розподілу Стьюдента (чи стандартного для великих вибірок) для заданого рівня значущості [math]\alpha[/math]. Для [math]n\le 60[/math] маємо [math]{{t}_{Kp}}={{t}_{Kp}}(\alpha ,d,f)[/math], а для [math]n\gt 60[/math] – наближену формулу [math]{{t}_{Kp}}=\psi (\alpha )[/math], де [math]\psi (\alpha )={{\Phi }^{-1}}(\alpha )[/math] - обернена функція стандартного закону розподілу.
6. Перевіряємо критерій: якщо [math]\left| t \right|\ge {{t}_{Kp}}[/math], то нульову гіпотезу відхиляємо, тобто існує суттєвий лінійний зв’язок між даними (дані корелюють). На практиці зручнішою є формула, яка дає критичне значення самого коефіцієнта кореляції. З рівняння статистики можна визначити [math]{{r}_{Kp}}=\frac{{{t}_{Kp}}}{\sqrt{n-2+t_{Kp}^{2}}}[/math] Ця формула дає змогу один раз відшукати критичне значення коефіцієнта кореляції (для фіксованого [math]\alpha[/math] і [math]n[/math]) і використовувати його в наступній серії порівнянь парних коефіцієнтів кореляції з критичним, наприклад, для перевірки на значущість коефіцієнтів кореляційної матриці.
Автокореляція
Автокореляція або автокореляційна функція - це кореляція функції з самою собою зміщеною на певну величину незалежної змінної. Автокореляція використовується для знаходження закономірностей в ряді даних, таких як періодичність. Часто застосовується у статистиці та обробці сигналів для аналізу функцій або серій даних. Математично автокореляційна функція визначається як:
[math]{{R}_{f}}(\tau )=\int\limits_{-\infty }^{\infty }{f(t){{f}^{*}}(t-\tau )}dt[/math],
де функція [math]f(t)[/math] інтегрується у добутку з комплексно спряженою та зміщеною на певну величину [math]\tau[/math] (часто [math]\tau[/math] це час) функцією.
Кореляційна матриця
Нехай маємо групу з [math]k[/math] випадкових змінних [math]{{x}_{1}},...,{{x}_{k}}[/math] (досліджуваних параметрів), що представлені вибірками обсягу [math]n[/math] кожна. Для усіх можливих різних пар індексів [math]i,j=1,2,...,k[/math] можна обчислити парні коефіцієнти кореляції [math]{{r}_{ij}}=r({{x}_{i}},{{x}_{j}})[/math]. Для [math]i=j[/math], тобто для двох ідентичних наборів, можна прийняти [math]{{r}_{i}}_{j}=1[/math], що відповідає лінійній функціональній залежності [math]{{x}_{i}}={{x}_{j}}[/math] (тотожності) для всіх пар значень у вибірках. Коефіцієнти кореляції запишемо у вигляді підсумкової симетричної матриці
[math]R=\left[ \begin{matrix} 1 & {{r}_{12}} & ... \\ {{r}_{21}} & 1 & ... \\ ... & ... & ... \\ {{r}_{k1}} & {{r}_{k2}} & ... \\ \end{matrix} \right..[/math]
Після перевірки кожного з коефіцієнтів на значущість (достатньо це зробити для елементів матриці над головною діагоналлю) і заміни коефіцієнтів, що менше [math]{{r}_{Kp}}[/math], нулем, “очищена” кореляційна матриця відображає “справжні” статистично значимі зв’язки між змінними. Аналіз структури кореляційної матриці є дуже важливим методом для виявлення, наприклад, парагенетичних асоціацій у геохімічних дослідженнях , а також основою інших методів аналізу (наприклад, факторного). З огляду на це часто виникає завдання порівняти різні коефіцієнти кореляції. Оскільки істинні коефіцієнти кореляції [math]{{\rho }_{i}}[/math], та [math]{{\rho }_{j}}[/math] невідомі, то рішення ухвалюють, користуючись їхніми вибірковими оцінками [math]{{r}_{i}}[/math] та [math]{{r}_{j}}[/math]на підставі статистичного доведення.
1. Формулюємо нульову гіпотезу про рівність коефіцієнтів кореляції
[math]{{H}_{0}}:{{\rho }_{i}}={{\rho }_{j}}[/math]
та альтернативну їй
[math]{{H}_{1}}:{{\rho }_{i}}\ne {{\rho }_{j}}[/math]
2. Вибираємо рівень значущості [math]\alpha[/math].
3. Оскільки розподіл коефіцієнтів кореляції за умови [math]\rho \ne 0[/math] має значну асиметрію, то використовуємо перетворені величини
[math]z{}_{i}=\frac{1}{2}\ln \frac{1+{{r}_{i}}}{1-{{r}_{i}}}[/math]
і будуємо статистику
[math]{{t}^{*}}=\frac{\left| {{z}_{i}}-{{z}_{j}} \right|}{s\sqrt{2}}[/math] [math]s=1/\sqrt{n-3}[/math]
4. В умовах гіпотези [math]{{H}_{0}}[/math] статистика [math]{{t}^{*}}[/math] має асимптотично нормальний розподіл з нульовим середнім та дисперсією, що дорівнює 1.
5. Знаходимо критичні значення статистики, тобто квантилі стандартного нормального розподілу, наприклад, для [math]\alpha =0,05[/math] маємо [math]{{t}^{*}}={{\psi }^{-1}}(0,05)=1,96[/math].
6. Якщо
[math]\left| {{z}_{i}}-{{z}_{j}} \right|\lt {{t}^{*}}s\sqrt{2}[/math]
то гіпотеза про рівність коефіцієнтів не суперечить вибірковим даним (для заданого [math]\alpha[/math]).
Список використаних джерел
- Курсова робота на тему: “Розробка методів для обчислення часткової кореляційної функції”.
- http://uk.wikipedia.org/wikiАвтокореляція
- http://www.lnu.edu.ua/faculty/geology/phis_geo/Khomyak/E-book_Geostatistics/Part2/Lections2-3-1.htm
- Аністенко В.О., Федоров В.Г. – Математичне планування експерименту АПК.

- Студент: Користувач:inna
- Виступ відбувся: 9 березня 2010
- Тема: Кореляційний аналіз експериментальних даних. Кореляційна матриця. Перевірка гіпотез відносно значень кореляційної матриці