Відмінності між версіями «Матриця планування експерименту»
| (Не показані 20 проміжних версій 8 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
| − | = | + | {{Невідредаговано}} |
| − | Перший етап планування експерименту для отримання лінійної моделі заснований на варіюванні факторів на двох рівнях.В цьому випадку, якщо кількість факторів відома, можна знайти кількість дослідів, необхідних для реалізації всіх можливих комбінацій рівнів факторів.Вона обчислюється за формулою | + | {{Студент | Name= Іван| Surname=Галас | FatherNAme=Михайлович |Faculti=ФІС | Group=СНм-51 | Zalbook=}} |
| + | |||
| + | {{Презентація доповіді |title=[http://elartu.tstu.edu.ua/handle/123456789 Матриця планування експеременту]}} | ||
| + | |||
| + | = Матриця планування експерименту = | ||
| + | В даному випадку розглядається планування першого порядку для якого ставляться такі вимоги: | ||
| + | *В якості факторів вибираються тільки контрольовані фактори. | ||
| + | *Забезпечується можливість незалежної зміни кожного з факторів і підтримання його на потрібному рівні. | ||
| + | *Для кожного фактору вказується інтервал(+/-) в межах якого проводиться експеримент. | ||
| + | Перед початком дослідів на основі апріорних даних вибирають рівень, який є базовим. Перший етап планування експерименту для отримання лінійної моделі заснований на варіюванні факторів на двох рівнях. | ||
| + | |||
| + | <center>[[Файл:G1.JPG]]</center> | ||
| + | |||
| + | В цьому випадку, якщо кількість факторів відома, можна знайти кількість дослідів, необхідних для реалізації всіх можливих комбінацій рівнів факторів.Вона обчислюється за формулою | ||
<math>N={{2}^{k}}</math>, де N - кількість дослідів, k - кількість факторів, 2 - кількість рівнів. В загальному випадку експеримент, в якому реалізуються всі можливі комбінації рівнів факторів, називається повним факторним експериментом. Якщо кількість рівнів кожного фактора два, то маємо повний факторний експеримент типу | <math>N={{2}^{k}}</math>, де N - кількість дослідів, k - кількість факторів, 2 - кількість рівнів. В загальному випадку експеримент, в якому реалізуються всі можливі комбінації рівнів факторів, називається повним факторним експериментом. Якщо кількість рівнів кожного фактора два, то маємо повний факторний експеримент типу | ||
<math>{{2}^{k}}</math> При плануванні експерименту проводять перетворення (нормалізацію) незалежних змінних | <math>{{2}^{k}}</math> При плануванні експерименту проводять перетворення (нормалізацію) незалежних змінних | ||
| Рядок 10: | Рядок 23: | ||
<math>{{z}_{iB}}=+1</math> та | <math>{{z}_{iB}}=+1</math> та | ||
<math>{{z}_{iH}}=-1</math>. | <math>{{z}_{iH}}=-1</math>. | ||
| − | Не важко записати всі комбінації рівнів при експерименті з двома факторами. Умови експерименту можна записати у вигляді таблиці, де рядки відповідають різноманітним дослідам, а стовпці - значенням факторів. Такі таблиці називаються матрицями планування експерименту.Кожен стовпець в матриці планування називають вектор -стовпцем, а кожен рядок вектор-рядком. Таким чином в таблиці і ми маємо два вектора-стовпці незалежних змінних(факторів) і один вектор стовпець параметра оптимізації. Те, що записано в цій таблиці в алгебраїчній формі, можна зобразити геометрично. В області визначення факторів шукається точка, яка відповідає основному рівню, і через неї проводяться нові осі координат, паралельні осям натуральних значень факторів. Далі, вибираються масштаби по нових осях так, щоб інтервал варіювання для кожного фактора дорівнював одиниці.Тоді умови проведення дослідів будуть відповідати вершинам квадрату, центром якого є основний рівень, а кожна сторона паралельна одній з осей координат і дорівнює двом інтервалам. Номери вершин квадрата відповідають номерам дослідів в матриці планування. Площа, обмежена квадратом, називається областю експерименту, або областю факторного простору. Іноді зручніше вважати областю експерименту площу, обмежену кругом,який описує квадрат. В задачах інтерполяції область експерименту є область можливих значень у. Запис матриці планування, особливо для багатьох факторів, громіздка. Для її скорочення зручно ввести умовні буквенні позначення рядків. Це робиться наступним чином. Порядковий номер фактора ставиться у відповідність маленькій букві латинського алфавіту: | + | Не важко записати всі комбінації рівнів при експерименті з двома факторами. Умови експерименту можна записати у вигляді таблиці, де рядки відповідають різноманітним дослідам, а стовпці - значенням факторів. |
| + | |||
| + | <center>[[Файл:G2.jpg]]</center> | ||
| + | |||
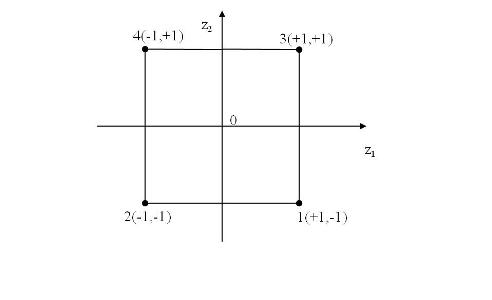
| + | Такі таблиці називаються матрицями планування експерименту.Кожен стовпець в матриці планування називають вектор -стовпцем, а кожен рядок вектор-рядком. Таким чином в таблиці і ми маємо два вектора-стовпці незалежних змінних(факторів) і один вектор стовпець параметра оптимізації. Те, що записано в цій таблиці в алгебраїчній формі, можна зобразити геометрично. | ||
| + | |||
| + | [[Файл:G4.JPG]] [[Файл:G3.JPG]] | ||
| + | |||
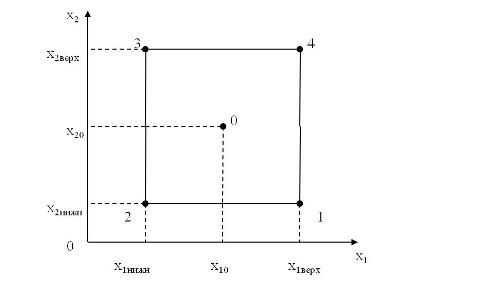
| + | В області визначення факторів шукається точка, яка відповідає основному рівню, і через неї проводяться нові осі координат, паралельні осям натуральних значень факторів. Далі, вибираються масштаби по нових осях так, щоб інтервал варіювання для кожного фактора дорівнював одиниці.Тоді умови проведення дослідів будуть відповідати вершинам квадрату, центром якого є основний рівень, а кожна сторона паралельна одній з осей координат і дорівнює двом інтервалам. Номери вершин квадрата відповідають номерам дослідів в матриці планування. Площа, обмежена квадратом, називається областю експерименту, або областю факторного простору. Іноді зручніше вважати областю експерименту площу, обмежену кругом,який описує квадрат. В задачах інтерполяції область експерименту є область можливих значень у. Областю факторного простору для трьохфакторного експерименту буде куб. | ||
| + | <center>[[Файл:G6.JPG]]</center> | ||
| + | Запис матриці планування, особливо для багатьох факторів, громіздка. Для її скорочення зручно ввести умовні буквенні позначення рядків. Це робиться наступним чином. Порядковий номер фактора ставиться у відповідність маленькій букві латинського алфавіту: | ||
<math>{{x}_{1}}-a,{{x}_{2}}-b,</math> і т.д. Якщо тепер для рядка матриці планування виписати латинські літери тільки для факторів, які знаходяться на верхніх рівнях, то умови досліду будуть задані однозначно. Дослід, при якому всі фактори знаходяться на нижніх рівнях позначають (1). | <math>{{x}_{1}}-a,{{x}_{2}}-b,</math> і т.д. Якщо тепер для рядка матриці планування виписати латинські літери тільки для факторів, які знаходяться на верхніх рівнях, то умови досліду будуть задані однозначно. Дослід, при якому всі фактори знаходяться на нижніх рівнях позначають (1). | ||
| + | |||
| + | <center>[[Файл:G5.JPG]]</center> | ||
| + | |||
| + | Таким чином ми побудували повний факторний експеримент | ||
| + | <math>{{2}^{3}}</math>. Він має вісім дослідів і включає всі можливі комбінації рівнів трьох факторів. Якщо для двох факторів всі можливі комбінації рівнів легко знайти прямим перебором, то з збільшенням кількості факторів виникає необхідність в деякому правилі побудови матриць. Серед багатьох можливих зазвичай використовуються три прийоми переходу від матриць меншої розмірності до матриць більшої розмірності: | ||
| + | *Записаний вихідний план для одного рівня вихідного фактора, а потім повторити його для другого рівня. | ||
| + | *Перемножуємо стовпці для вихідного плану, записуєм для половини дослідів, потім міняєм знаки отриманого вектора на протилежні і записуємо для другої половини дослідів. | ||
| + | *В першому стовпці знаки міняються через один,в другому міняються через два рази, в третьому через чотири, в четвертому через вісім і т.д. | ||
| + | Властивості матриці планування експерименту: | ||
| + | * Властивість симетричності – алгебраїчна сума элементів вектор-стовпця кожного фактора рівна нулю. | ||
| + | |||
| + | <center><math>\sum\limits_{j=1}^{n}{{{x}_{ij}}=0}</math></center> | ||
| + | |||
| + | * Властивість нормування – сума квадратів елементів кожного стовпця рівна кількості дослідів. | ||
| + | |||
| + | <center><math>\sum\limits_{j=1}^{n}{{{x}_{ij}}^{2}=n}</math></center> | ||
| + | |||
| + | * Властивість ортогональності – скалярний добуток всіх вектор-стовпців(сума почленних добутків елементів будь-яких вектор-стовпців) рівна нулю. | ||
| + | |||
| + | <center><math>\sum\limits_{j=1}^{n}{{{x}_{ij}}{{x}_{uj}}=0,i\ne u}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | =Список використаних джерел= | ||
| + | #Аністратенко В.О., Федоров В.Г. /Математичне планування експериментів в АПК: Навч. посібник.-К.Вища шк., 1993.-375 с. | ||
| + | #Ю.П.Адлер, Е.В.Маркова, Ю.В.Грановский /Планирование експеримента при поиске оптимальних условий:М.Наука, 1976.-280 с. | ||
| + | #Монтгоиери Д.К. /Планированиє експеримента и анализ данных: Пер. с англ.-Л:.Судостроение, 1980.-384 с. | ||
| + | #Е.Т. Володарский, Б.Н. Малиновский, Ю.М. Туз-К./Планирование и организация измерительного експреимента:Вища шк.Головное изд-во, 1987.-280 с. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | {{Завдання:Виступ|Scoolf|9 березня 2010|Матриця планування експерименту}} | ||
| + | |||
| + | [[Категорія:Виступ на семінарі]] | ||
| + | [[Категорія:Планування експерименту]] | ||
Поточна версія на 10:05, 20 березня 2012
| Цю статтю потрібно відредагувати. Щоб вона відповідала ВИМОГАМ. |
| {{{img}}} | ||
| Імя | Іван | |
| Прізвище | Галас | |
| По-батькові | Михайлович | |
| Факультет | ФІС | |
| Група | СНм-51 | |
| Залікова книжка | ||
| Презентація доповіді на тему Матриця планування експеременту є розміщеною в Репозиторії. |
Матриця планування експерименту
В даному випадку розглядається планування першого порядку для якого ставляться такі вимоги:
- В якості факторів вибираються тільки контрольовані фактори.
- Забезпечується можливість незалежної зміни кожного з факторів і підтримання його на потрібному рівні.
- Для кожного фактору вказується інтервал(+/-) в межах якого проводиться експеримент.
Перед початком дослідів на основі апріорних даних вибирають рівень, який є базовим. Перший етап планування експерименту для отримання лінійної моделі заснований на варіюванні факторів на двох рівнях.
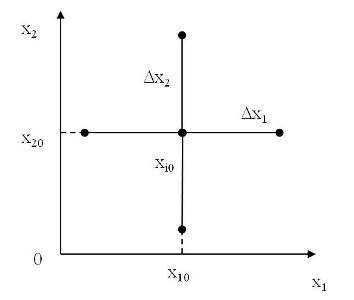
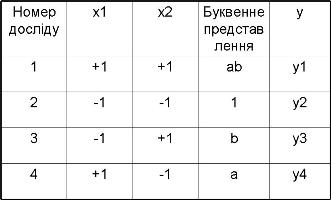
В цьому випадку, якщо кількість факторів відома, можна знайти кількість дослідів, необхідних для реалізації всіх можливих комбінацій рівнів факторів.Вона обчислюється за формулою [math]N={{2}^{k}}[/math], де N - кількість дослідів, k - кількість факторів, 2 - кількість рівнів. В загальному випадку експеримент, в якому реалізуються всі можливі комбінації рівнів факторів, називається повним факторним експериментом. Якщо кількість рівнів кожного фактора два, то маємо повний факторний експеримент типу [math]{{2}^{k}}[/math] При плануванні експерименту проводять перетворення (нормалізацію) незалежних змінних [math]{{z}_{i}}[/math]: [math]{{z}_{i}}=\frac{{{x}_{i}}-{{x}_{i0}}}{\Delta {{x}_{i}}}[/math], що дає можливість легко побудувати ортогональну матрицю планування і полегшує подальші обчислення, оскільки верхній та нижній рівні варіювання [math]{{z}_{iB}}[/math] при [math]{{x}_{i0}}\lt {{x}_{i}}[/math] та [math]{{z}_{iH}}[/math] при [math]{{x}_{i0}}\gt {{x}_{i}}[/math] дорівнюють відповідно [math]{{z}_{iB}}=+1[/math] та [math]{{z}_{iH}}=-1[/math]. Не важко записати всі комбінації рівнів при експерименті з двома факторами. Умови експерименту можна записати у вигляді таблиці, де рядки відповідають різноманітним дослідам, а стовпці - значенням факторів.
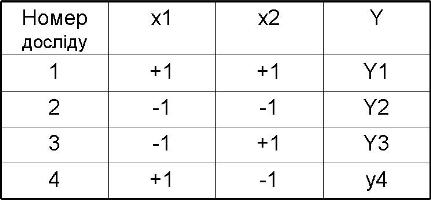
Такі таблиці називаються матрицями планування експерименту.Кожен стовпець в матриці планування називають вектор -стовпцем, а кожен рядок вектор-рядком. Таким чином в таблиці і ми маємо два вектора-стовпці незалежних змінних(факторів) і один вектор стовпець параметра оптимізації. Те, що записано в цій таблиці в алгебраїчній формі, можна зобразити геометрично.
В області визначення факторів шукається точка, яка відповідає основному рівню, і через неї проводяться нові осі координат, паралельні осям натуральних значень факторів. Далі, вибираються масштаби по нових осях так, щоб інтервал варіювання для кожного фактора дорівнював одиниці.Тоді умови проведення дослідів будуть відповідати вершинам квадрату, центром якого є основний рівень, а кожна сторона паралельна одній з осей координат і дорівнює двом інтервалам. Номери вершин квадрата відповідають номерам дослідів в матриці планування. Площа, обмежена квадратом, називається областю експерименту, або областю факторного простору. Іноді зручніше вважати областю експерименту площу, обмежену кругом,який описує квадрат. В задачах інтерполяції область експерименту є область можливих значень у. Областю факторного простору для трьохфакторного експерименту буде куб.
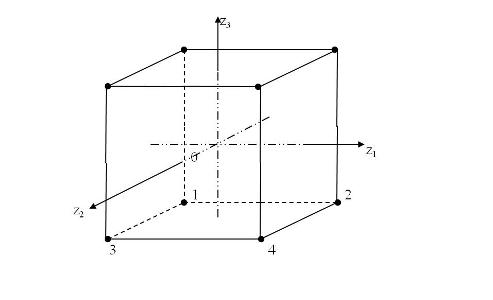
Запис матриці планування, особливо для багатьох факторів, громіздка. Для її скорочення зручно ввести умовні буквенні позначення рядків. Це робиться наступним чином. Порядковий номер фактора ставиться у відповідність маленькій букві латинського алфавіту: [math]{{x}_{1}}-a,{{x}_{2}}-b,[/math] і т.д. Якщо тепер для рядка матриці планування виписати латинські літери тільки для факторів, які знаходяться на верхніх рівнях, то умови досліду будуть задані однозначно. Дослід, при якому всі фактори знаходяться на нижніх рівнях позначають (1).
Таким чином ми побудували повний факторний експеримент [math]{{2}^{3}}[/math]. Він має вісім дослідів і включає всі можливі комбінації рівнів трьох факторів. Якщо для двох факторів всі можливі комбінації рівнів легко знайти прямим перебором, то з збільшенням кількості факторів виникає необхідність в деякому правилі побудови матриць. Серед багатьох можливих зазвичай використовуються три прийоми переходу від матриць меншої розмірності до матриць більшої розмірності:
- Записаний вихідний план для одного рівня вихідного фактора, а потім повторити його для другого рівня.
- Перемножуємо стовпці для вихідного плану, записуєм для половини дослідів, потім міняєм знаки отриманого вектора на протилежні і записуємо для другої половини дослідів.
- В першому стовпці знаки міняються через один,в другому міняються через два рази, в третьому через чотири, в четвертому через вісім і т.д.
Властивості матриці планування експерименту:
- Властивість симетричності – алгебраїчна сума элементів вектор-стовпця кожного фактора рівна нулю.
- Властивість нормування – сума квадратів елементів кожного стовпця рівна кількості дослідів.
- Властивість ортогональності – скалярний добуток всіх вектор-стовпців(сума почленних добутків елементів будь-яких вектор-стовпців) рівна нулю.
Список використаних джерел
- Аністратенко В.О., Федоров В.Г. /Математичне планування експериментів в АПК: Навч. посібник.-К.Вища шк., 1993.-375 с.
- Ю.П.Адлер, Е.В.Маркова, Ю.В.Грановский /Планирование експеримента при поиске оптимальних условий:М.Наука, 1976.-280 с.
- Монтгоиери Д.К. /Планированиє експеримента и анализ данных: Пер. с англ.-Л:.Судостроение, 1980.-384 с.
- Е.Т. Володарский, Б.Н. Малиновский, Ю.М. Туз-К./Планирование и организация измерительного експреимента:Вища шк.Головное изд-во, 1987.-280 с.

- Студент: Користувач:Scoolf
- Виступ відбувся: 9 березня 2010
- Тема: Матриця планування експерименту