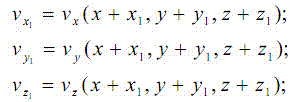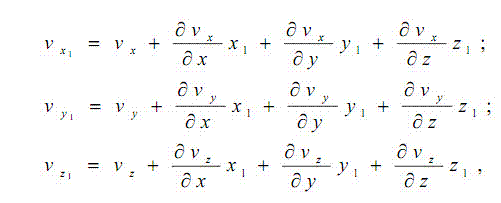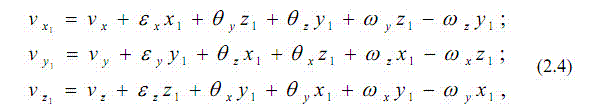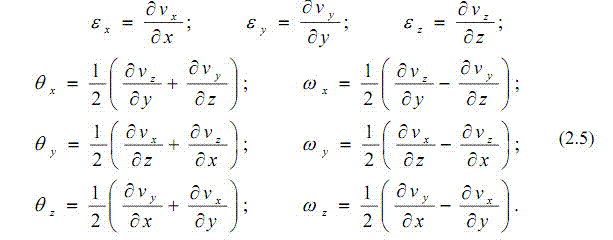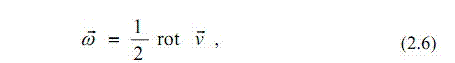Відмінності між версіями «Теорема Коші-Гельмгольца»
Natasha (обговорення • внесок) |
Natasha (обговорення • внесок) |
||
| (Не показано 10 проміжних версій цього користувача) | |||
| Рядок 1: | Рядок 1: | ||
З теоретичної механіки відомо, що в загальному випадку рух | З теоретичної механіки відомо, що в загальному випадку рух | ||
твердого тіла в кожен момент складається з поступального переміщення полюса і обертання навколо миттєвої осі, що проходить через цей | твердого тіла в кожен момент складається з поступального переміщення полюса і обертання навколо миттєвої осі, що проходить через цей | ||
| − | полюс. Рух рідини більш | + | полюс. Рух рідини більш складний. Кожна рідка частинка, крім |
поступального переміщення і обертання, зазнає ще й деформації. | поступального переміщення і обертання, зазнає ще й деформації. | ||
Для вивчення всіх складових руху розглянемо нескінченно | Для вивчення всіх складових руху розглянемо нескінченно | ||
| − | малу рідку | + | малу рідку частинку в довільний момент часу (рис. 1). |
Позначимо проекції швидкості у точці М(x,y,z) – центрі частинки, | Позначимо проекції швидкості у точці М(x,y,z) – центрі частинки, | ||
прийнятому за полюс, через <math>v_x(x,y,z)</math> ; <math>v_y(x,y,z)</math>; <math>v_z(x,y,z)</math>. Тоді в деякій | прийнятому за полюс, через <math>v_x(x,y,z)</math> ; <math>v_y(x,y,z)</math>; <math>v_z(x,y,z)</math>. Тоді в деякій | ||
| Рядок 16: | Рядок 16: | ||
[[Файл:A2.gif]] рис. 1 Частинка рідини у різних системах координат | [[Файл:A2.gif]] рис. 1 Частинка рідини у різних системах координат | ||
| + | |||
| + | Розкладемо функції швидкостей <math>v_x,v_y,v_z </math>в ряди Тейлора по степеням <math>x_1, y_1, z_1</math> в окрузі точки | ||
| + | М(x,y,z). Утримуючи члени до першого порядку малости включно, отримаємо | ||
| + | |||
| + | [[Файл:A3.gif]] | ||
| + | |||
| + | де для скорочення запису, замість <math>v_x(x,y,z)</math> записано <math>v_x</math> и т. д. | ||
| + | Після нескладних перетворень можна отримати | ||
| + | |||
| + | [[Файл:A4.gif]], | ||
| + | |||
| + | де | ||
| + | |||
| + | [[Файл:A5.gif]] | ||
| + | |||
| + | Вияснимо фізичний зміст кожного із складових в (2.4): | ||
| + | - <math>v_x, v_y</math> і <math>v_z</math> - проекції поступальної швидкості центру рідкої частинки; | ||
| + | - пари останніх складових(<math>w_yz_1, w_zy_1</math> та ін.) – проекції швидкості руху частинок навколо миттєвої осі, що проходить через її центр. Такий обертовий рух частинки в гідромеханіці називають вихровим, а проекції кутової швидкості обертання <math>w_x, w_y, w_z</math> - компонентами вихoру (ротора). Із векторного аналізу і формул (2.5) випливає, що кутова швидкість | ||
| + | |||
| + | [[Файл:A6.gif]] | ||
| + | |||
| + | де rot<math> v</math> - вихор швидкості; | ||
| + | |||
| + | - три складові, які залишились кожної із формул (2.4) пов'язані із деформацією рідкої частинки у часі. Величини <math>\varepsilon_x,\varepsilon_y,\varepsilon_z</math> характеризують швидкості деформації розтягнення (стиску) рідкої частинки, а | ||
| + | <math>\theta_x, \theta_y, \theta_z</math> - швидкості деформації зсуву (перекосу). | ||
Все описане тут і становить суть теореми Коші-Гельмгольца: швидкість будь-якої рідкої частки складається з швидкості полюса, швидкості обертання навколо миттєвої осі, що проходить через цей полюс, а також швидкості деформаційного руху, що складається з лінійної деформації і деформації зсуву. | Все описане тут і становить суть теореми Коші-Гельмгольца: швидкість будь-якої рідкої частки складається з швидкості полюса, швидкості обертання навколо миттєвої осі, що проходить через цей полюс, а також швидкості деформаційного руху, що складається з лінійної деформації і деформації зсуву. | ||
Поточна версія на 16:51, 6 червня 2011
З теоретичної механіки відомо, що в загальному випадку рух твердого тіла в кожен момент складається з поступального переміщення полюса і обертання навколо миттєвої осі, що проходить через цей полюс. Рух рідини більш складний. Кожна рідка частинка, крім поступального переміщення і обертання, зазнає ще й деформації. Для вивчення всіх складових руху розглянемо нескінченно малу рідку частинку в довільний момент часу (рис. 1). Позначимо проекції швидкості у точці М(x,y,z) – центрі частинки, прийнятому за полюс, через [math]v_x(x,y,z)[/math] ; [math]v_y(x,y,z)[/math]; [math]v_z(x,y,z)[/math]. Тоді в деякій точці M1 із координатами [math](x+x_1, y+y_1, z+z_1)[/math] на поверхні частинки проекції швидкості можуть бути записані у вигляді
де [math]x_1, y_1[/math] і [math]z_1[/math] в силу малих розмірів частинки являються нескінченно малими величинами
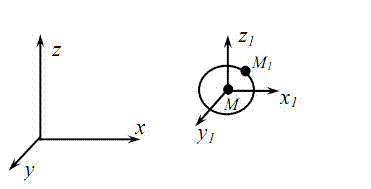 рис. 1 Частинка рідини у різних системах координат
рис. 1 Частинка рідини у різних системах координат
Розкладемо функції швидкостей [math]v_x,v_y,v_z[/math]в ряди Тейлора по степеням [math]x_1, y_1, z_1[/math] в окрузі точки М(x,y,z). Утримуючи члени до першого порядку малости включно, отримаємо
де для скорочення запису, замість [math]v_x(x,y,z)[/math] записано [math]v_x[/math] и т. д. Після нескладних перетворень можна отримати
де
Вияснимо фізичний зміст кожного із складових в (2.4): - [math]v_x, v_y[/math] і [math]v_z[/math] - проекції поступальної швидкості центру рідкої частинки; - пари останніх складових([math]w_yz_1, w_zy_1[/math] та ін.) – проекції швидкості руху частинок навколо миттєвої осі, що проходить через її центр. Такий обертовий рух частинки в гідромеханіці називають вихровим, а проекції кутової швидкості обертання [math]w_x, w_y, w_z[/math] - компонентами вихoру (ротора). Із векторного аналізу і формул (2.5) випливає, що кутова швидкість
де rot[math]v[/math] - вихор швидкості;
- три складові, які залишились кожної із формул (2.4) пов'язані із деформацією рідкої частинки у часі. Величини [math]\varepsilon_x,\varepsilon_y,\varepsilon_z[/math] характеризують швидкості деформації розтягнення (стиску) рідкої частинки, а [math]\theta_x, \theta_y, \theta_z[/math] - швидкості деформації зсуву (перекосу).
Все описане тут і становить суть теореми Коші-Гельмгольца: швидкість будь-якої рідкої частки складається з швидкості полюса, швидкості обертання навколо миттєвої осі, що проходить через цей полюс, а також швидкості деформаційного руху, що складається з лінійної деформації і деформації зсуву.