Відмінності між версіями «Досліди Рейнольдса»
Durbu (обговорення • внесок) |
|||
| (Не показані 57 проміжних версій 2 користувачів) | |||
| Рядок 1: | Рядок 1: | ||
| − | '''Дослідами Рейнольдса встановлено''', що за певних граничних умов у кожному потоці є "точка переходу", яка відповідає зміні одного режиму іншим. Ця точка переходу за Рейнольдсом визначається безрозмірним комплексом - числом Рейнольдса Re, яке називається критичним числом Рейнольдса. Рух буде ламінарний, коли Re<Re | + | '''Дослідами Рейнольдса встановлено''', що за певних граничних умов у кожному потоці є "точка переходу", яка відповідає зміні одного режиму іншим. Ця точка переходу за Рейнольдсом визначається безрозмірним комплексом - числом Рейнольдса <math>\operatorname{Re}</math>, яке називається критичним числом Рейнольдса. Рух буде ламінарний, коли <math>\operatorname{Re} < {\operatorname{Re} _{kr}}</math>. Якщо <math>\operatorname{Re} > {\operatorname{Re} _{kr}}</math>, то потік стає нестаціонарним і переходить у турбулентний режим. При русі рідини у прямоліній циліндричній трубі <math>\operatorname{Re} _{kr} = 2300</math>. Для кожного конкретного випадку руху число Рейнольдса має своє критичне значення. |
== Історія дослідження == | == Історія дослідження == | ||
| Рядок 5: | Рядок 5: | ||
На принципову різницю ламінарного і турбулентного руху рідини звернув увагу Д.І. Менделєєв у 1880 р. і М.П. Петров у 1883 р. Однак найбільш глибоко і повно це питання було досліджене у 1883 р. англійським фізиком О.Рейнольдсом. Після Рейнольдса багатьма дослідниками було виконано ряд теоретичних та експерементальних праць щодо вивчення переходу ламінарного режиму в турбулентний, і навпаки, в різних умовах. Незважаючи на це, дане питання і на цей час вивчене недостатньо; багато питань переходу одного режиму в інший та природа турбулентного режиму залишаються і тепер не зовсім зрозумілими. | На принципову різницю ламінарного і турбулентного руху рідини звернув увагу Д.І. Менделєєв у 1880 р. і М.П. Петров у 1883 р. Однак найбільш глибоко і повно це питання було досліджене у 1883 р. англійським фізиком О.Рейнольдсом. Після Рейнольдса багатьма дослідниками було виконано ряд теоретичних та експерементальних праць щодо вивчення переходу ламінарного режиму в турбулентний, і навпаки, в різних умовах. Незважаючи на це, дане питання і на цей час вивчене недостатньо; багато питань переходу одного режиму в інший та природа турбулентного режиму залишаються і тепер не зовсім зрозумілими. | ||
| − | == Ламінарний і турбулентний | + | == Ламінарний і турбулентний режими руху == |
[[Файл:18.png|150px|thumb|right|Схематичний вигляд ламінарного руху]] | [[Файл:18.png|150px|thumb|right|Схематичний вигляд ламінарного руху]] | ||
Гідравлічна структура потоків при цих двох режимах істотно відрізняється. При ламінарному режимі окремі частинки рідини переміщються паралельно одна одній і окремі струминки потоку переміщуються упорядковано. При цьому режимі течій в циліндричних шарів, які, подібно до окремих частин телескопічної труби, переміщуються. | Гідравлічна структура потоків при цих двох режимах істотно відрізняється. При ламінарному режимі окремі частинки рідини переміщються паралельно одна одній і окремі струминки потоку переміщуються упорядковано. При цьому режимі течій в циліндричних шарів, які, подібно до окремих частин телескопічної труби, переміщуються. | ||
| Рядок 19: | Рядок 19: | ||
Результати багатьох досліджень показують, що ламінарний рух у певних умовах стає нестабільним і переходить у турбулентний під впливом навіть незначних зовнішніх збурень. Ламінарний режим переходит у турбулентний через так званий '''''перехідний режим''''', а сам процес переходу в більшості випадків можна розглядати як безперервний коливний процес. | Результати багатьох досліджень показують, що ламінарний рух у певних умовах стає нестабільним і переходить у турбулентний під впливом навіть незначних зовнішніх збурень. Ламінарний режим переходит у турбулентний через так званий '''''перехідний режим''''', а сам процес переходу в більшості випадків можна розглядати як безперервний коливний процес. | ||
| + | Ретельно усунувши збурення при вході в трубу (рис. 50, вузол Д), можна значно збільшити критичне число Рейнольдса (навіть до 20000 і вище). У зв'язку з цим деколи вводять поняття про нижнє і верхнє число Рейнольдса: при цьому під нижнім критичним числом розуміють нижню границю <math>\operatorname{Re}</math> для турбулентного руху, а під верхнім - верхню границю для ламінарного руху. Значення <math>\operatorname{Re} _{kr} = 2300</math> приймається за нижню границю для турбулентного руху, а <math>\operatorname{Re} _{kr} = 4000...20000</math> дає діапазон зміни верхнього критичного числа <math>\operatorname{Re} _{kr}</math>. | ||
| − | + | При <math>\operatorname{Re} < {\operatorname{Re} _{kr}}</math> будь-якого роду збурення в потоці гасяться силами в'язкості і ламінарний режим в цілому стійкий, а турбулентний - нестійкий. При <math>\operatorname{Re} > {\operatorname{Re} _{kr}}</math>, навпаки, турбулентний режим стійкий, а ламінарний - нестійкий. Далі під критичним числом <math>\operatorname{Re} _{kr}</math> будемо розуміти тільки нижнє критичне число. | |
| + | Звернемо увагу на те, що для труб некруглого перерізу, відкритих русел, лотків число Рейнольдса виражається через '''гідравлічний радіус''' <math>\operatorname{R}</math>- відношення площі живого перерізу до змоченого периметра в цьому перерізі, тобто | ||
| − | + | <math>Re=\frac{{VR}}{\nu } </math> | |
| − | <math>\ | + | У даному разі критичне число <math>\operatorname{Re} _{kr} = 580</math> |
| − | + | ==Фактори які впливають на критичне значення числа Рейнольдса== | |
| − | + | На величину <math>\operatorname{Re} _{kr}</math> впливає ряд факторів: умова входу в трубу, знак прискорення, з яким рухається рідина, кривина труби тощо.Наприклад, <math>\operatorname{Re} _{kr}</math> значно знижується навіть при невеликому викривленні труби. Місця розширення трубопроводу або русел мають підвищену схильність до порушення ламінарного режиму.Необхідно зазначити, що значеня критичного числа Рейнольдса залежить від ряду умов, як наприклад від обурення, створюваного в джерелі живлення трубопроводу, від обурень при вході рідини в трубопровід і інших обурень, які створюються в самому трубопроводі. На ці обурення впливає шорсткість трубопроводу. Крім цього, на значення критичного числа Re істотний вплив має і то як воно визначилось. Досвід показує, що відновлення ламінарного руху при переході до нього з турбулентного виникає при значно менших значеннях Re, чим руйнує ламінарний рух при переході його до турбулентного. В умовах лабораторної обстановки вдалось зберегти ламінарний рух при числах Re, перевищуючих 50000. Все ж це представляє собою тільки теоретичний інтерес. В інженерній практиці, особливо в коротких трубопроводах, не завжди вдається зберегти ламінарний рух навіть при Re=2000. Навпаки, наявність різних пристроїв в трубопровідних комунікаціях зменшує критичне значення. Загальноприйнятим критичним значенням вважається Re=2320 | |
| − | + | Однак, завжди потрібно мати на увазі, що в розрахунках із значенням Re, яке знаходиться поблизу критичного <math>\operatorname{Re} _{kr}</math>, потрібно ретельно аналізувати всі умови , які можуть вплинути на режим руху. | |
| + | == Число Рейнольдса == | ||
| + | |||
| + | Знайти число Рейнольдса можна за формулою: | ||
| + | |||
| + | <math>\operatorname{Re} = \frac{{\rho VL}}{\eta } = \frac{{VL}}{\nu } = \frac{{QL}}{{\nu A}}</math> | ||
| + | |||
| + | де | ||
| + | |||
| + | * <math>\rho \</math> - густина середовища; | ||
| + | * <math>V\</math> - характерна швидкість; | ||
| + | * <math>L\</math> - характрений розмір; | ||
| + | * <math>\eta \</math> - динамічна в'язкість середовища; | ||
| + | * <math>\nu \</math> - кінематична в'язкість середовища; | ||
| + | * <math>A\</math> - площ січення труби; | ||
| + | * <math>Q\</math> - об'ємна швидкість потоку. | ||
| + | |||
| + | == Використання числа Рейнольдса і його значення == | ||
| + | |||
| + | Число Рейнольдса дуже корисне з точки зору моделювання потоків в різних рідинах і газах, оскільки їх поведінка залежить не від реальної в’язкості, густини, швидкості і лінійних розмірів елемента потоку, а лише від їхнього відношення, вираженого числом Рейнольдса. Завдяки цьому можна, наприклад, помістити в аеродинамічну трубу зменшену модель літака і підібрати швидкість потоку таким чином, щоб число Рейнольдса відповідало реальній ситуації повномасштабного літака в польоті. Взагалі критерій Рейнольдса є необхідним інструментом для визначення коефіцієнтів тепловіддачі, масопередачі і тертя в процесах за участі ріди і газів.Для проектувальника опалення і вентиляції він зручний тим, що дозволяє порахувати коефіцієнт тертя для рідин і газів за одною формулою, підставляючи відповідні значення Re. | ||
== Література == | == Література == | ||
Поточна версія на 18:47, 19 травня 2012
Дослідами Рейнольдса встановлено, що за певних граничних умов у кожному потоці є "точка переходу", яка відповідає зміні одного режиму іншим. Ця точка переходу за Рейнольдсом визначається безрозмірним комплексом - числом Рейнольдса [math]\operatorname{Re}[/math], яке називається критичним числом Рейнольдса. Рух буде ламінарний, коли [math]\operatorname{Re} \lt {\operatorname{Re} _{kr}}[/math]. Якщо [math]\operatorname{Re} \gt {\operatorname{Re} _{kr}}[/math], то потік стає нестаціонарним і переходить у турбулентний режим. При русі рідини у прямоліній циліндричній трубі [math]\operatorname{Re} _{kr} = 2300[/math]. Для кожного конкретного випадку руху число Рейнольдса має своє критичне значення.
Зміст
Історія дослідження
Ще у минулому столітті було зауважено, що при русі рідини можуть бути два принципово різні режими руху рідини - ламінарний і турбулентний ( слово "ламінарний" походить від латинського "lamina", що означає "шаруватий"; турбулентний - від латинського "turbulentus", що означає вихровий, безладний.) На принципову різницю ламінарного і турбулентного руху рідини звернув увагу Д.І. Менделєєв у 1880 р. і М.П. Петров у 1883 р. Однак найбільш глибоко і повно це питання було досліджене у 1883 р. англійським фізиком О.Рейнольдсом. Після Рейнольдса багатьма дослідниками було виконано ряд теоретичних та експерементальних праць щодо вивчення переходу ламінарного режиму в турбулентний, і навпаки, в різних умовах. Незважаючи на це, дане питання і на цей час вивчене недостатньо; багато питань переходу одного режиму в інший та природа турбулентного режиму залишаються і тепер не зовсім зрозумілими.
Ламінарний і турбулентний режими руху
Гідравлічна структура потоків при цих двох режимах істотно відрізняється. При ламінарному режимі окремі частинки рідини переміщються паралельно одна одній і окремі струминки потоку переміщуються упорядковано. При цьому режимі течій в циліндричних шарів, які, подібно до окремих частин телескопічної труби, переміщуються. Ламінарний рух рідин зустрічається в трубках невеликого діаметра при переміщенні дуже в'язких рідин. В інженерній практиці у більшості випадків спостерігається рух рідини при турбулентному режимі, характреною ознакою якого є безладний характер переміщення окремих частинок. При турбулентному режимі в кожній точці простору, зайнятого рідиною, що рухається, відбувається безперервна зміна швидкості як за значенням, так і за напрямком.Така зміна швидкості називається пульсацією швидкості, яка, в свою чергу, викликає пульсацію тиску. У зв'язку з цим турбулентний потік - це безліч мас, які інтенсивно обертаються і переміщуються, при загальному поступальному русі.
Експеримент Рейнольдса
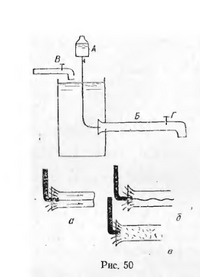
Експеримент Рейнольдса полягав у введені барвника з посудини А (рис.50) у скляну трубу Б і спостереженні за течією окремих струминок. Було виявлено, що за певних умов забарвлена струминка рухається прямолінійно, без змішування з навколишньою масою рідини. Інакше кажучи, спостерігався ламінарний рух (рис. 50,а). Далі збільшення швидкості (шляхом відповідного регулювання вентилями В і Г) приводить до зміни характеру руху частинок рідини. Забарвлена струминка зі збільшенням шивдкості стає звивистою (рис. 50,б), хиткою, в окремих місцях уривчастою, а відтак повністю розмивається і зміщується з усією масою рідини, що рухається в трубі (рис. 50,в). Виникає турбулентний режим з притаманним йому інтенсивним переміщенням частинок рідини по всьому перерізу потоку.
Результати багатьох досліджень показують, що ламінарний рух у певних умовах стає нестабільним і переходить у турбулентний під впливом навіть незначних зовнішніх збурень. Ламінарний режим переходит у турбулентний через так званий перехідний режим, а сам процес переходу в більшості випадків можна розглядати як безперервний коливний процес. Ретельно усунувши збурення при вході в трубу (рис. 50, вузол Д), можна значно збільшити критичне число Рейнольдса (навіть до 20000 і вище). У зв'язку з цим деколи вводять поняття про нижнє і верхнє число Рейнольдса: при цьому під нижнім критичним числом розуміють нижню границю [math]\operatorname{Re}[/math] для турбулентного руху, а під верхнім - верхню границю для ламінарного руху. Значення [math]\operatorname{Re} _{kr} = 2300[/math] приймається за нижню границю для турбулентного руху, а [math]\operatorname{Re} _{kr} = 4000...20000[/math] дає діапазон зміни верхнього критичного числа [math]\operatorname{Re} _{kr}[/math].
При [math]\operatorname{Re} \lt {\operatorname{Re} _{kr}}[/math] будь-якого роду збурення в потоці гасяться силами в'язкості і ламінарний режим в цілому стійкий, а турбулентний - нестійкий. При [math]\operatorname{Re} \gt {\operatorname{Re} _{kr}}[/math], навпаки, турбулентний режим стійкий, а ламінарний - нестійкий. Далі під критичним числом [math]\operatorname{Re} _{kr}[/math] будемо розуміти тільки нижнє критичне число. Звернемо увагу на те, що для труб некруглого перерізу, відкритих русел, лотків число Рейнольдса виражається через гідравлічний радіус [math]\operatorname{R}[/math]- відношення площі живого перерізу до змоченого периметра в цьому перерізі, тобто
[math]Re=\frac{{VR}}{\nu }[/math]
У даному разі критичне число [math]\operatorname{Re} _{kr} = 580[/math]
Фактори які впливають на критичне значення числа Рейнольдса
На величину [math]\operatorname{Re} _{kr}[/math] впливає ряд факторів: умова входу в трубу, знак прискорення, з яким рухається рідина, кривина труби тощо.Наприклад, [math]\operatorname{Re} _{kr}[/math] значно знижується навіть при невеликому викривленні труби. Місця розширення трубопроводу або русел мають підвищену схильність до порушення ламінарного режиму.Необхідно зазначити, що значеня критичного числа Рейнольдса залежить від ряду умов, як наприклад від обурення, створюваного в джерелі живлення трубопроводу, від обурень при вході рідини в трубопровід і інших обурень, які створюються в самому трубопроводі. На ці обурення впливає шорсткість трубопроводу. Крім цього, на значення критичного числа Re істотний вплив має і то як воно визначилось. Досвід показує, що відновлення ламінарного руху при переході до нього з турбулентного виникає при значно менших значеннях Re, чим руйнує ламінарний рух при переході його до турбулентного. В умовах лабораторної обстановки вдалось зберегти ламінарний рух при числах Re, перевищуючих 50000. Все ж це представляє собою тільки теоретичний інтерес. В інженерній практиці, особливо в коротких трубопроводах, не завжди вдається зберегти ламінарний рух навіть при Re=2000. Навпаки, наявність різних пристроїв в трубопровідних комунікаціях зменшує критичне значення. Загальноприйнятим критичним значенням вважається Re=2320 Однак, завжди потрібно мати на увазі, що в розрахунках із значенням Re, яке знаходиться поблизу критичного [math]\operatorname{Re} _{kr}[/math], потрібно ретельно аналізувати всі умови , які можуть вплинути на режим руху.
Число Рейнольдса
Знайти число Рейнольдса можна за формулою:
[math]\operatorname{Re} = \frac{{\rho VL}}{\eta } = \frac{{VL}}{\nu } = \frac{{QL}}{{\nu A}}[/math]
де
- [math]\rho \[/math] - густина середовища;
- [math]V\[/math] - характерна швидкість;
- [math]L\[/math] - характрений розмір;
- [math]\eta \[/math] - динамічна в'язкість середовища;
- [math]\nu \[/math] - кінематична в'язкість середовища;
- [math]A\[/math] - площ січення труби;
- [math]Q\[/math] - об'ємна швидкість потоку.
Використання числа Рейнольдса і його значення
Число Рейнольдса дуже корисне з точки зору моделювання потоків в різних рідинах і газах, оскільки їх поведінка залежить не від реальної в’язкості, густини, швидкості і лінійних розмірів елемента потоку, а лише від їхнього відношення, вираженого числом Рейнольдса. Завдяки цьому можна, наприклад, помістити в аеродинамічну трубу зменшену модель літака і підібрати швидкість потоку таким чином, щоб число Рейнольдса відповідало реальній ситуації повномасштабного літака в польоті. Взагалі критерій Рейнольдса є необхідним інструментом для визначення коефіцієнтів тепловіддачі, масопередачі і тертя в процесах за участі ріди і газів.Для проектувальника опалення і вентиляції він зручний тим, що дозволяє порахувати коефіцієнт тертя для рідин і газів за одною формулою, підставляючи відповідні значення Re.
Література
- Левицький Б.Ф., Лещій Н.П. Гідравліка.Загальний курс - Львів: Cвіт,1994.-264с.
- Т.М. Башта, С.С Руднев Гидравлика, гидромашины и гидроприводы,1982.-423с
- Френкель Н.З. Гидравлика 1956.-456с
- Кочин Н.Е Теоретическая гидромеханика.Часть 1-2,1963-585с